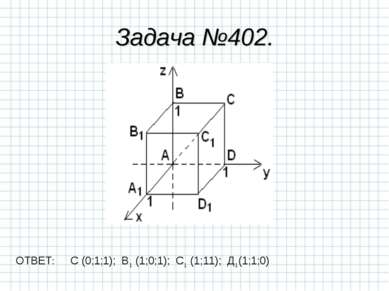
X
Код презентации скопируйте его
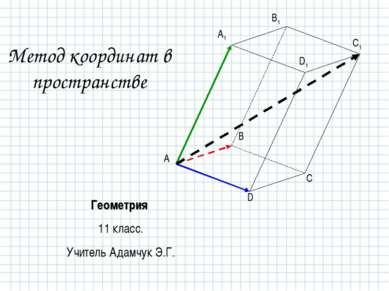
Метод координат в пространстве (11 класс)
Скачать эту презентацию
Презентация на тему Метод координат в пространстве (11 класс)
Скачать эту презентациюCлайд 1
Метод координат в пространстве Геометрия 11 класс. Учитель Адамчук Э.Г. A B C D A1 B1 C1 D1
Cлайд 2
Цели урока: 1.Повторить понятия вектора; 2.Ввести понятие прямоугольной системы координат в пространстве. Задачи урока: выработать умения строить точку по заданным её координатам и находить координаты точки, изображённой в заданной системе координат.
Cлайд 3
Содержание урока: Повторение понятия вектора; Прямоугольная система координат; Понятия координат векторов; Решение задач координатным методом; Домашнее задание.
Cлайд 4
Как и в плоскости, в пространстве вектор определяется как направленный отрезок: A B Точка А – начало вектора, В – конец вектора. Записывают: или . a Вектор, у которого начало совпадает с конечной точкой называется нулевым, обозначается: или . Длина отрезка, изображающего вектор, называется модулем вектора, т.е. Определение вектора.
Cлайд 5
Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то говорят, что задана система координат в пространстве.
Cлайд 6
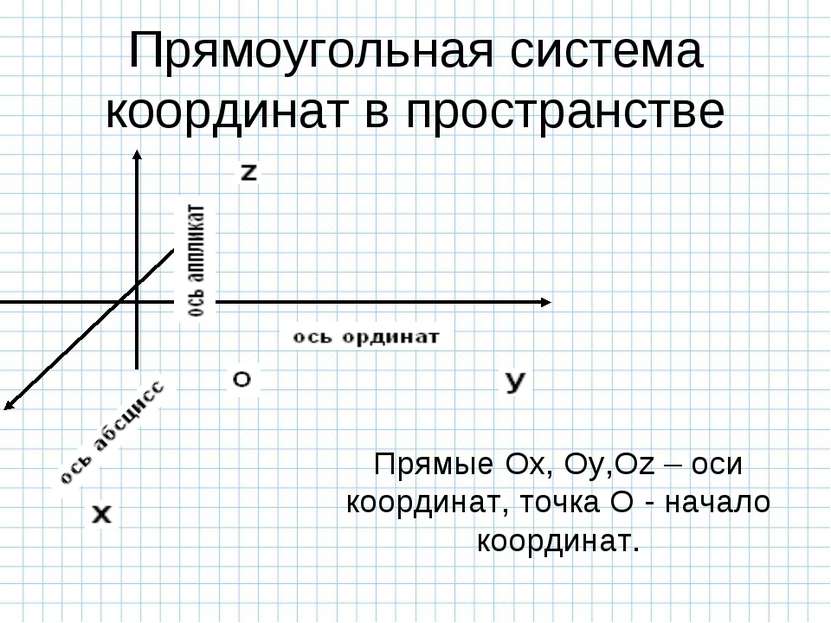
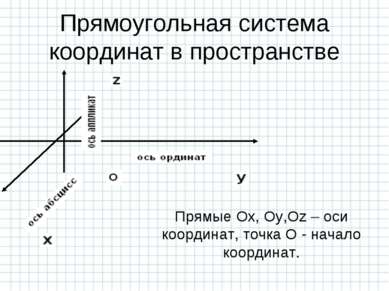Прямоугольная система координат в пространстве Прямые Ox, Oy,Oz – оси координат, точка О - начало координат.
Cлайд 7
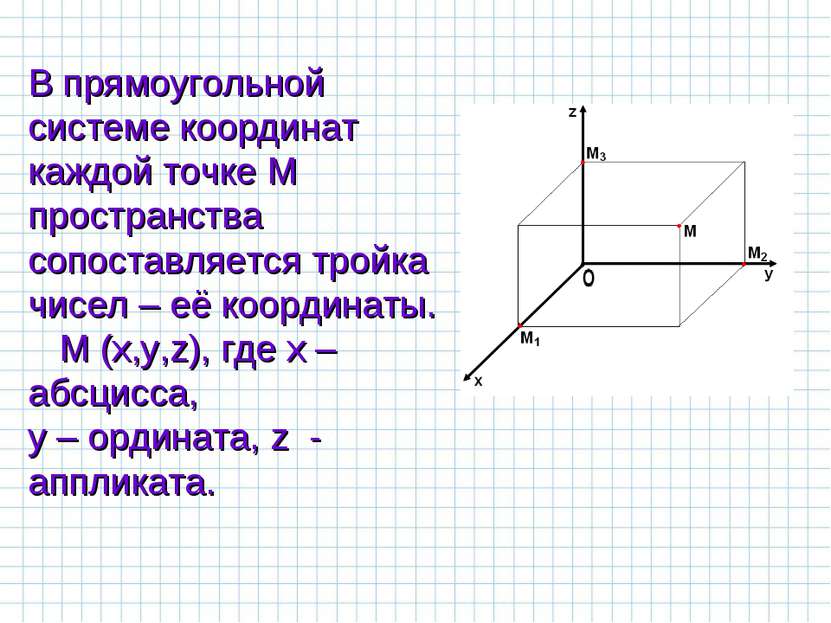
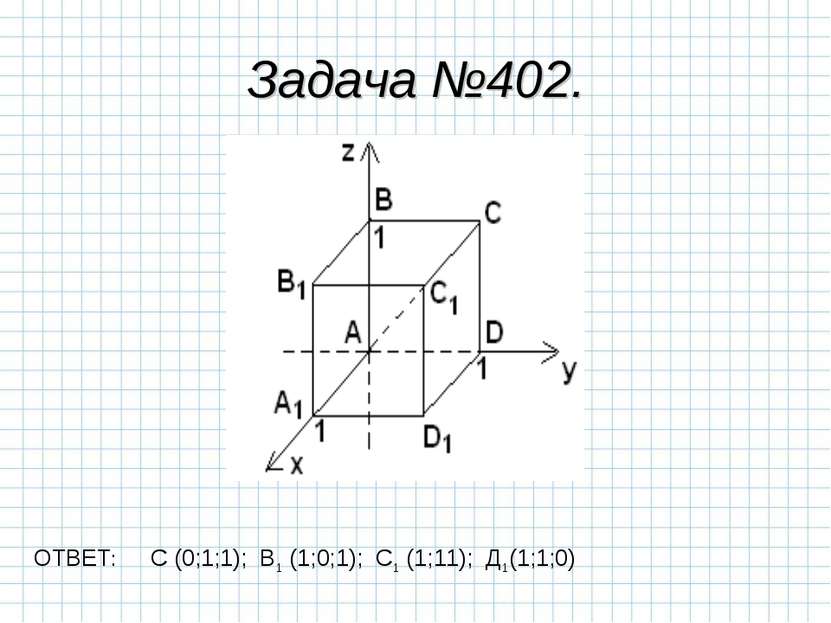
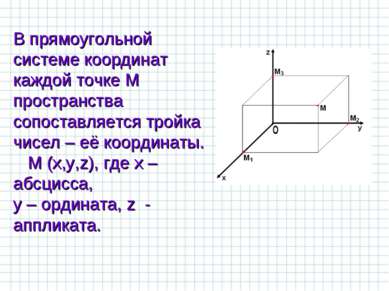В прямоугольной системе координат каждой точке М пространства сопоставляется тройка чисел – её координаты. М (х,у,z), где х – абсцисса, у – ордината, z - аппликата.
Cлайд 8
А1 (2;-3;0); А2 (2;0;5); А3 (0;-3;5) Задача №401. ОТВЕТ :
Cлайд 9
Задача №402. ОТВЕТ: С (0;1;1); В1 (1;0;1); С1 (1;11); Д1(1;1;0)
Cлайд 10
Домашнее задание. Выучить §42. №400 д); е), № 403, №407 е),ж), з).
Cлайд 11
Координаты вектора Цель урока: Изучить метод координат.
Cлайд 12
План урока: Дать понятие единичных векторов; Рассмотреть правила сложения, вычитания, умножения; Решение задач; Домашняя работа.
Cлайд 13
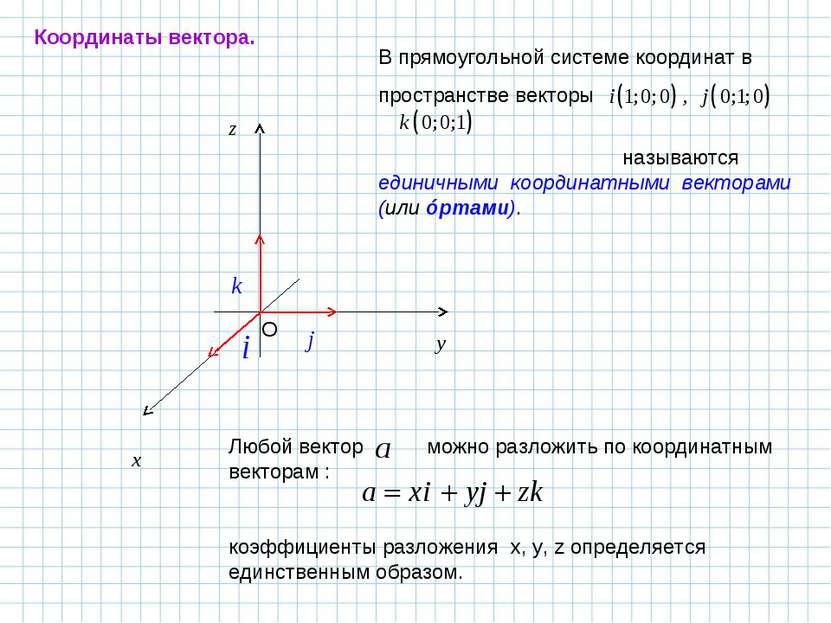
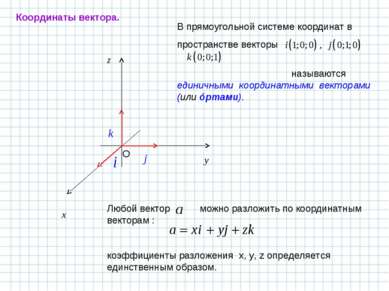В прямоугольной системе координат в пространстве векторы называются единичными координатными векторами (или óртами). x z O Любой вектор можно разложить по координатным векторам : коэффициенты разложения x, y, z определяется единственным образом. y Координаты вектора.
Cлайд 14
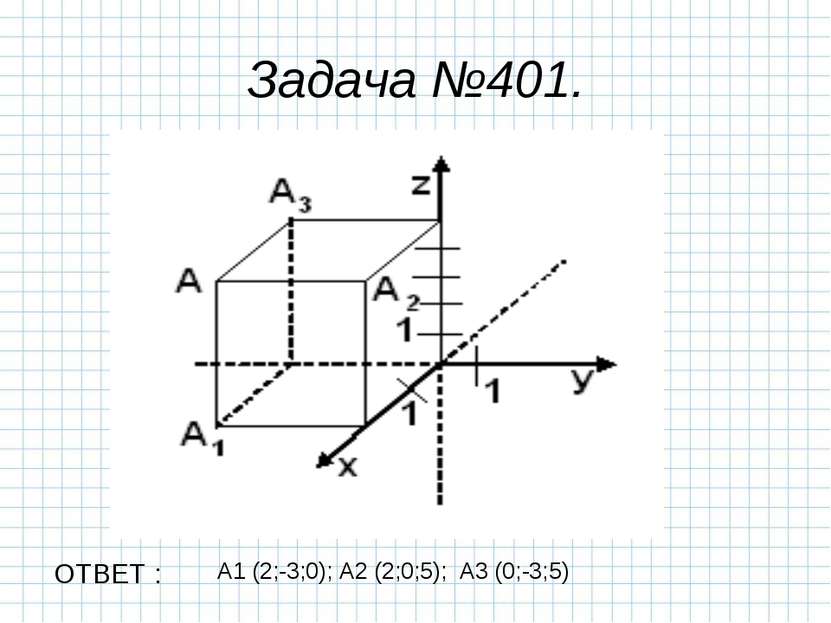
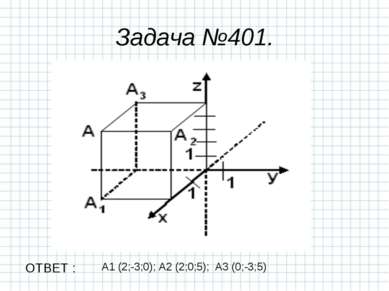
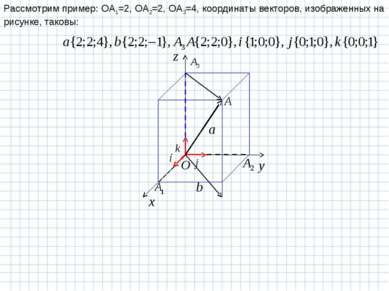Рассмотрим пример: OA1=2, OA2=2, OA3=4, координаты векторов, изображенных на рисунке, таковы:
Cлайд 15
10. Каждая координата суммы 2х или более векторов равна сумме соответствующих координат этих векторов, т.е. 20. Каждая координата разности 2х векторов равна разности соответствующих координат этих векторов, т.е. 30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Cлайд 16
Задача Даны векторы: Найти координаты векторов: Решение: 1. 2. И 3. Ответ:
Cлайд 17
Самостоятельная работа Вариант 1 Найти координаты векторов: Вариант 2 Найти координаты векторов: Даны векторы:
Cлайд 18
Домашнее задание §43; Доказать одно из утверждений 10-30. № 407 е), ж), з); №409 а)-м).
