X
Код презентации скопируйте его
Построение сечений многогранников (10 класс)
Скачать эту презентацию
Презентация на тему Построение сечений многогранников (10 класс)
Скачать эту презентациюCлайд 1
Презентация на тему: Построение сечений многогранника. Выполнила ученица 10 класса Пименова Ксения. Учитель математики: Мазалова Лариса Сергеевна.
Cлайд 2
Содержание Определение. Примеры построений сечений. Задания на построение сечений.
Cлайд 3
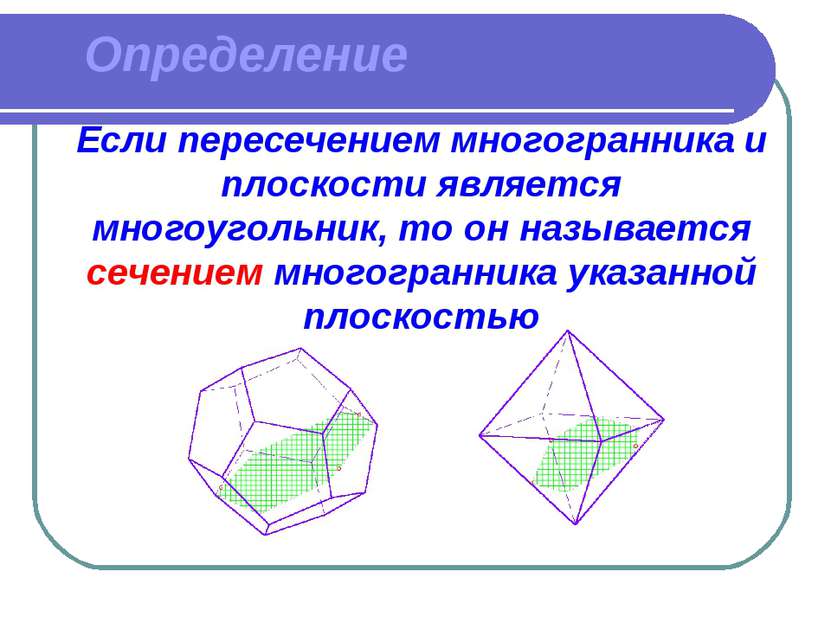
Определение Если пересечением многогранника и плоскости является многоугольник, то он называется сечением многогранника указанной плоскостью
Cлайд 4
Сечение пирамид. Пирамида – это многогранник, одна из граней которого – произвольный многоугольник. Тетраэдр - это многогранник, одна из граней которого – произвольный треугольник. Так как тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырехугольники.
Cлайд 5
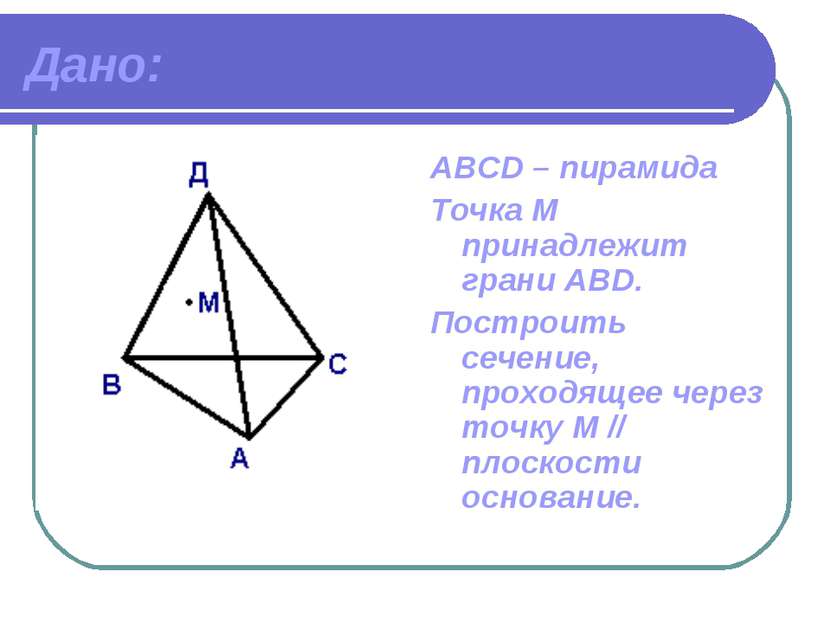
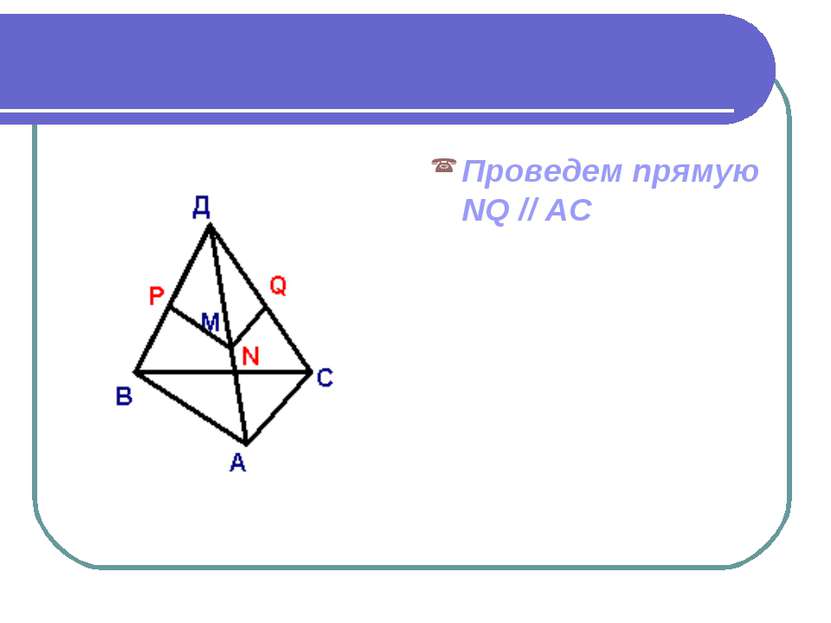
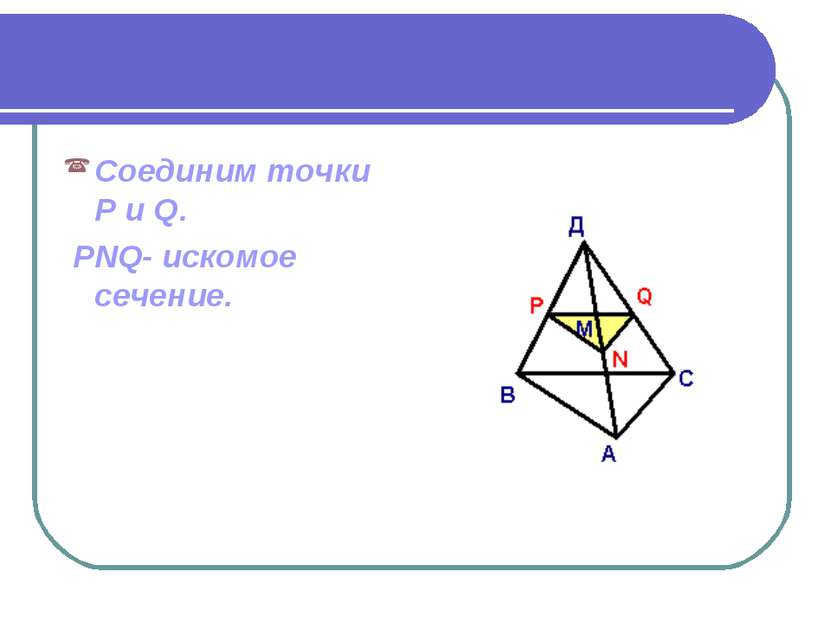
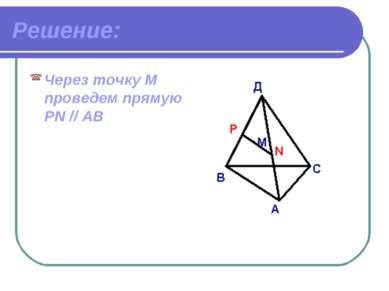
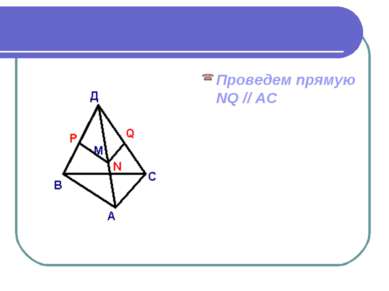
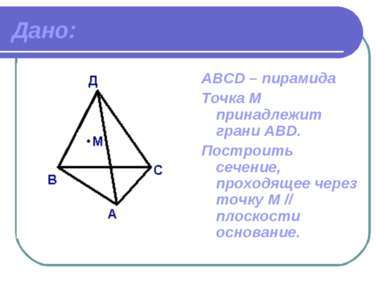Дано: АВСD – пирамида Точка М принадлежит грани ABD. Построить сечение, проходящее через точку М // плоскости основание.
Cлайд 6
Решение: Через точку М проведем прямую PN // АВ
Cлайд 7
Проведем прямую NQ // AC
Cлайд 8
Соединим точки P и Q. PNQ- искомое сечение.
Cлайд 9
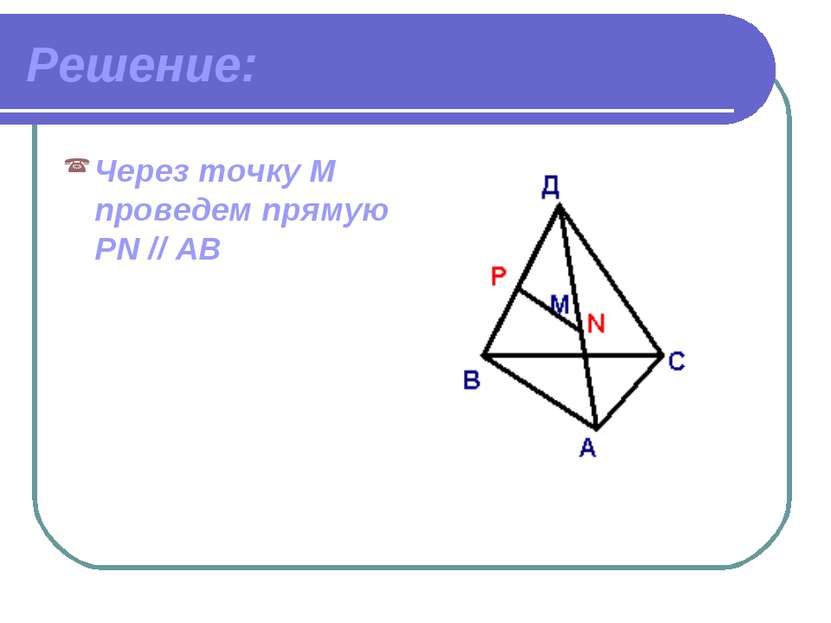
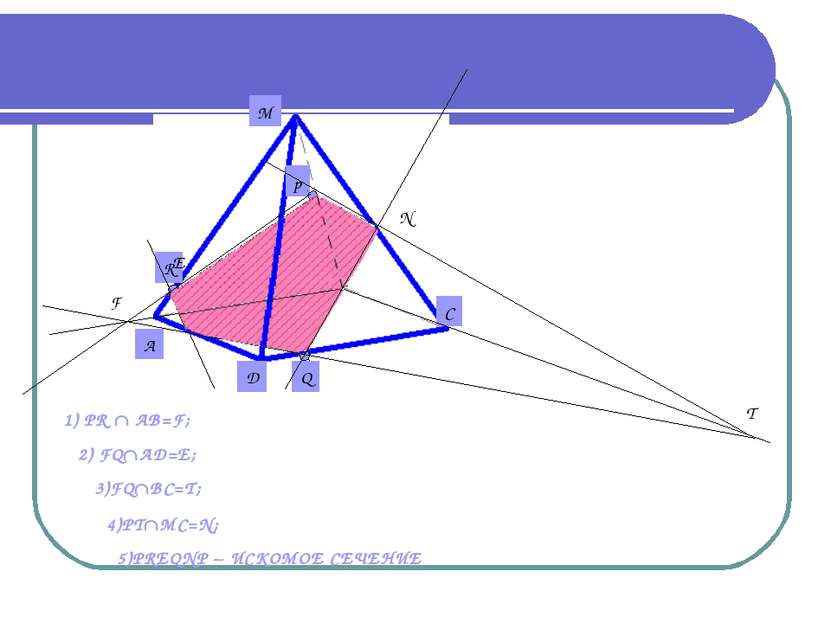
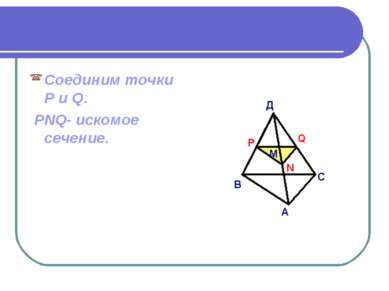
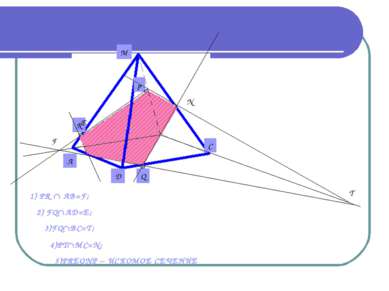
Дано: Пирамида MABCD. Постройте сечение пирамиды, проходящее через точки P, Q, R. Известно, что точка P MB, точка R MA, Q DC. ВАЖНО! Если секущая плоскость пересекает противоположные грани, то она пересекает их по параллельным отрезкам.
Cлайд 10
F T 1) PR AB=F; 2) FQ AD=E; 3)FQ BC=T; 4)PT MC=N; 5)PREQNP – ИСКОМОЕ СЕЧЕНИЕ Е N
Cлайд 11
Сечение куба Прямоугольный параллелепипед, у которого все три измерения равны, называется кубом. Куб имеет 6 граней. Его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.
Cлайд 12
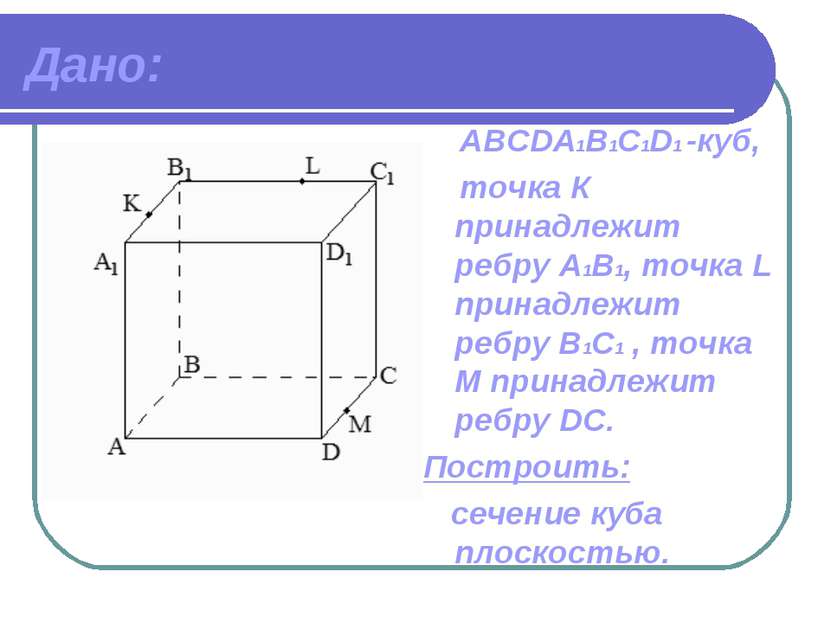
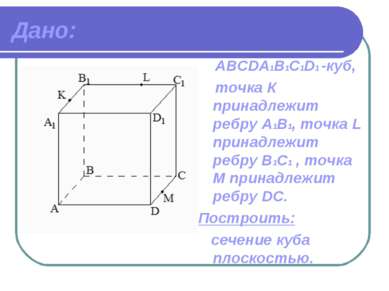Дано: ABCDА1B1C1D1 -куб, точка К принадлежит ребру A1В1, точка L принадлежит ребру В1C1 , точка М принадлежит ребру DC. Построить: сечение куба плоскостью.
Cлайд 13
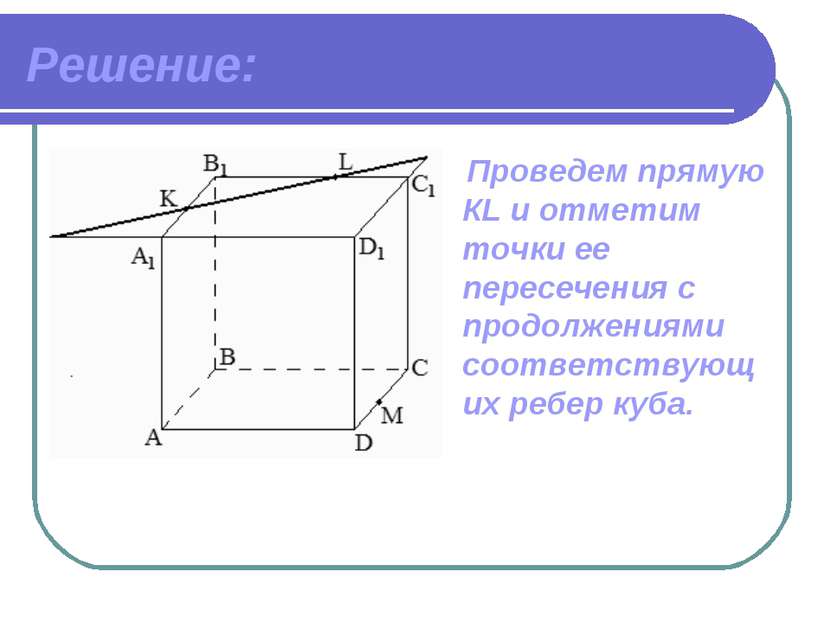
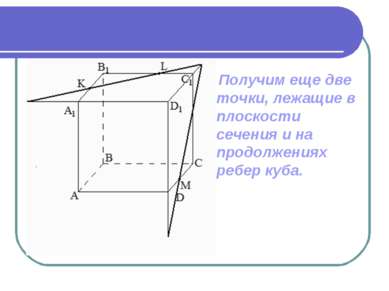
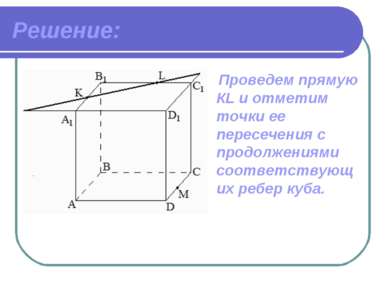Решение: Проведем прямую КL и отметим точки ее пересечения с продолжениями соответствующих ребер куба.
Cлайд 14
Получим еще две точки, лежащие в плоскости сечения и на продолжениях ребер куба.
Cлайд 15
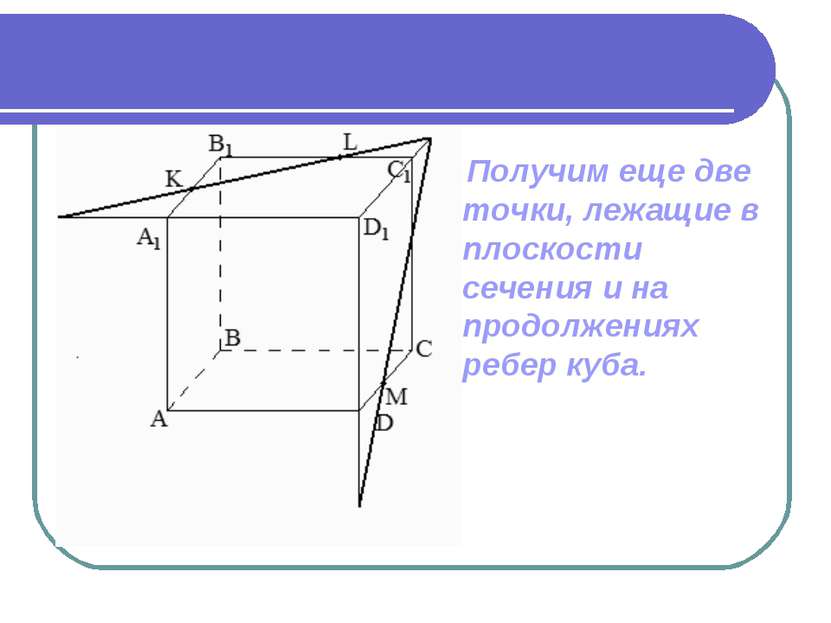
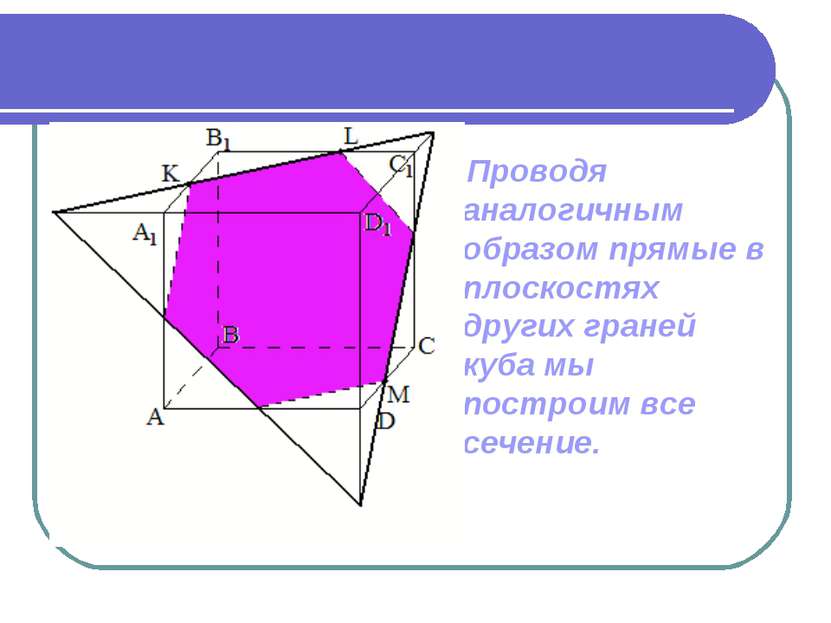
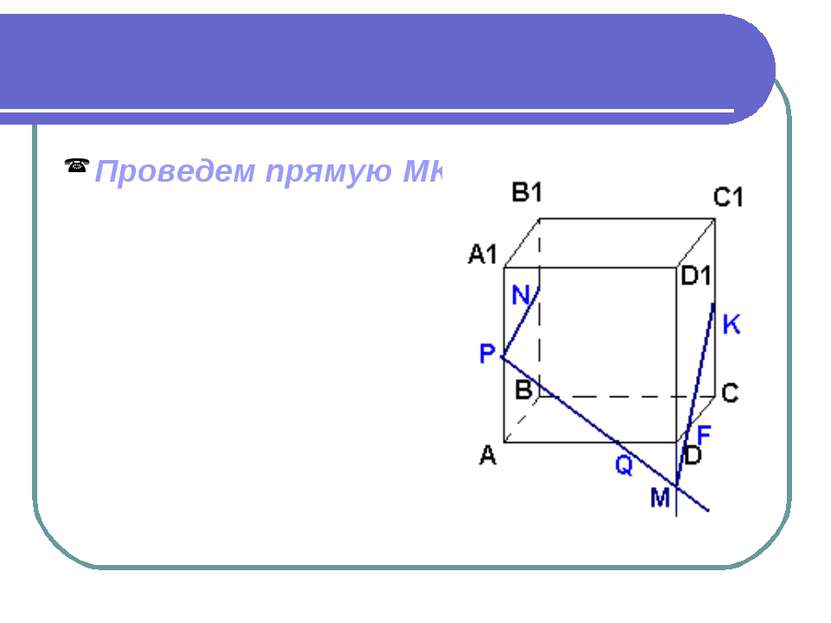
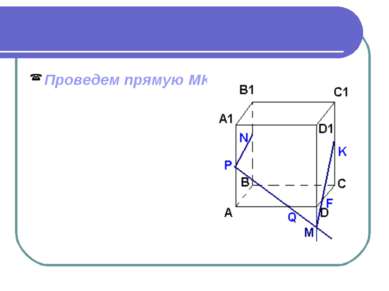
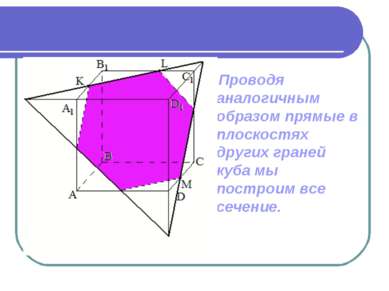Проводя аналогичным образом прямые в плоскостях других граней куба мы построим все сечение.
Cлайд 16
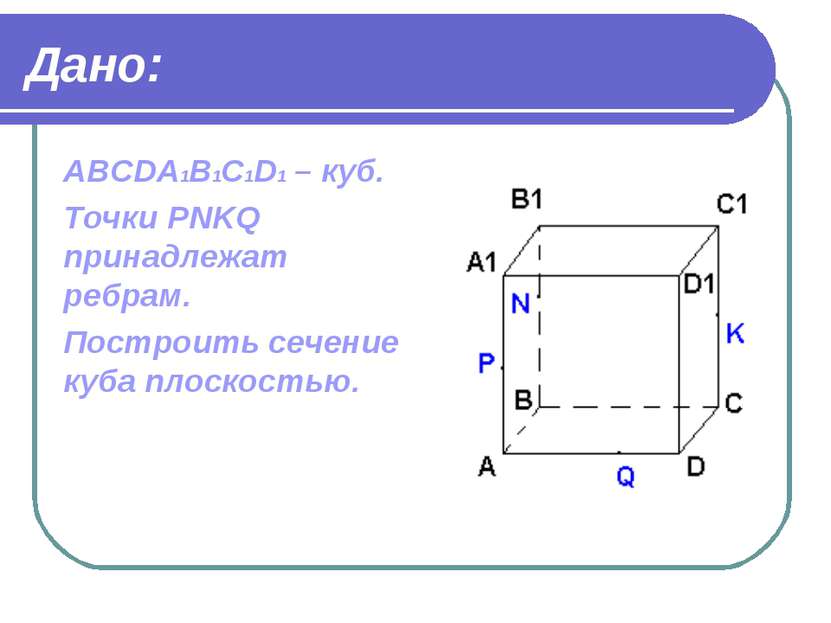
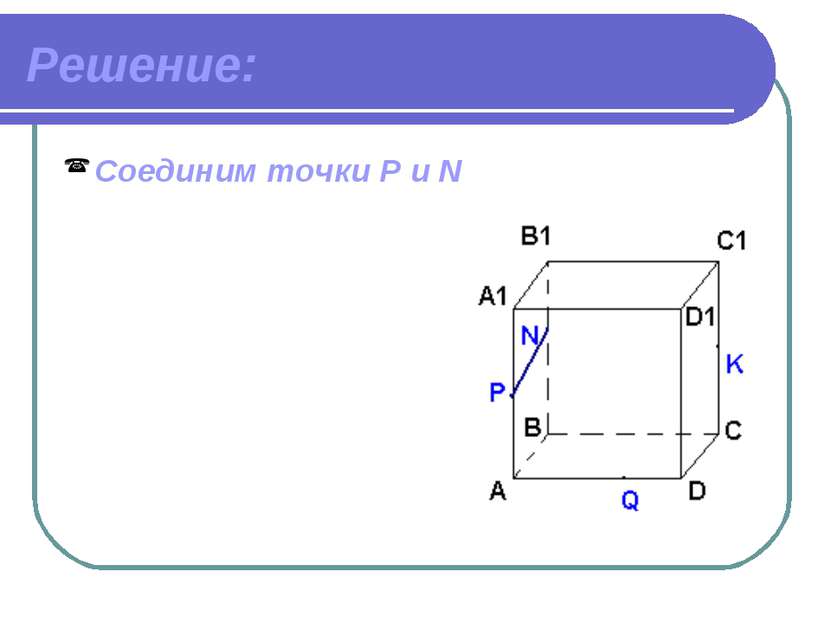
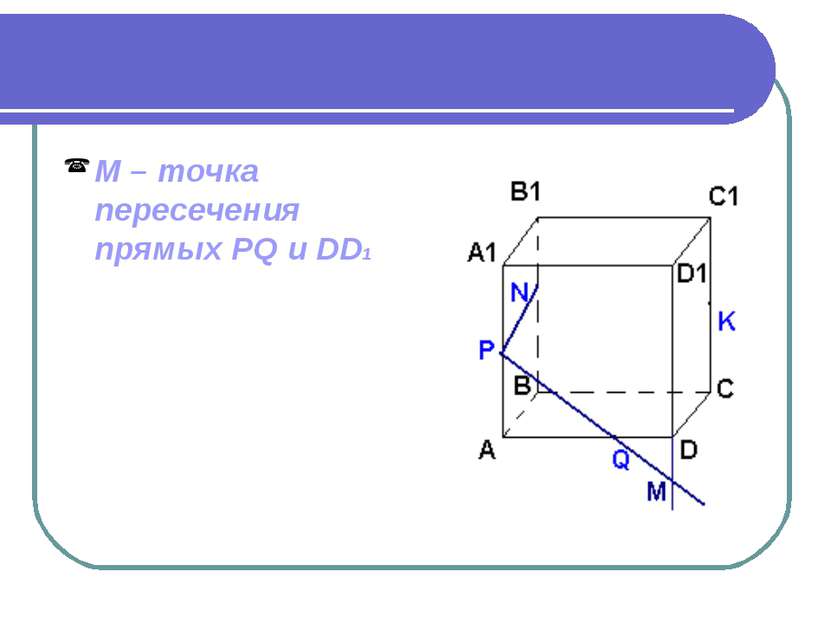
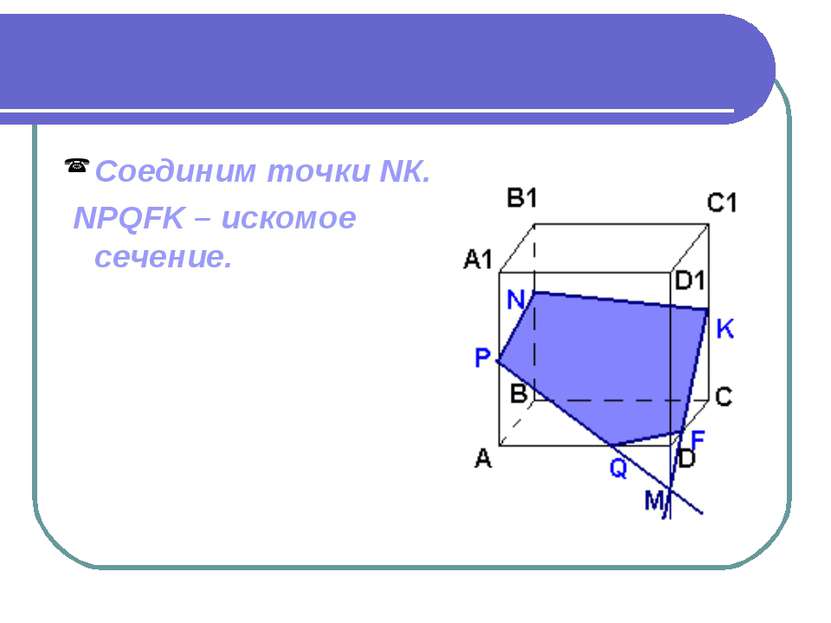
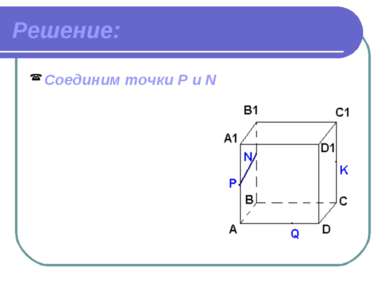
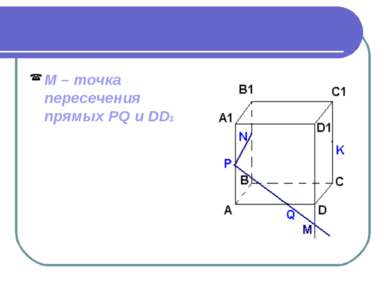
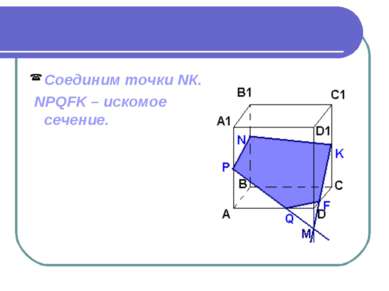
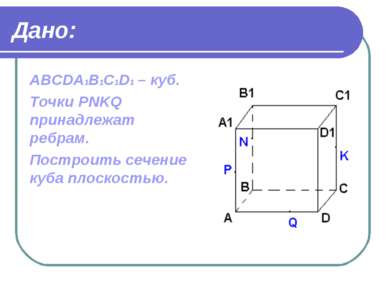Дано: ABCDA1B1C1D1 – куб. Точки PNKQ принадлежат ребрам. Построить сечение куба плоскостью.
Cлайд 17
Решение: Соединим точки P и N
Cлайд 18
М – точка пересечения прямых PQ и DD1
Cлайд 19
Проведем прямую МК
Cлайд 20
Соединим точки NК. NPQFK – искомое сечение.
Cлайд 21
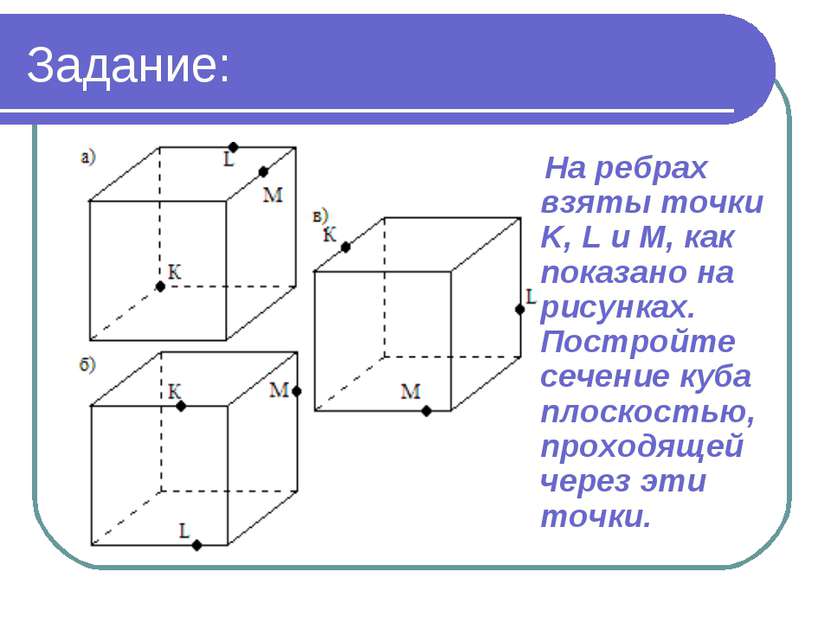
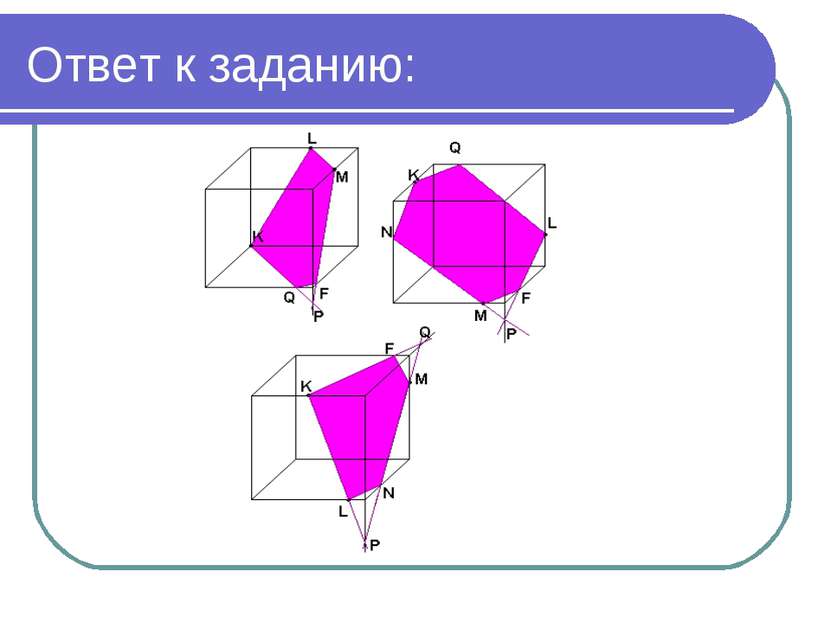
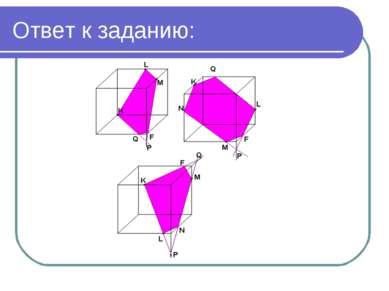
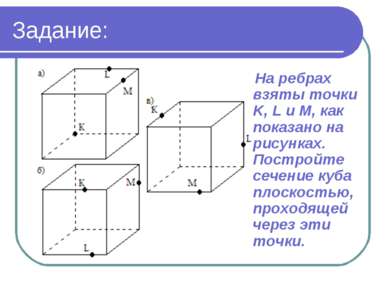Задание: На ребрах взяты точки K, L и M, как показано на рисунках. Постройте сечение куба плоскостью, проходящей через эти точки.
Cлайд 22
Ответ к заданию:
Cлайд 23
Cлайд 24
«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» Л.Кэрролл
Cлайд 25
За каждым многогранником закреплено его значение, НАПРИМЕР: Тетраэдр является огнём!
Cлайд 26
куб-земля
Cлайд 27
октаэдр-воздух
Cлайд 28
Даже пчёлы знакомы с понятием многогранник!!!
Cлайд 29
Многогранники в архитектуре. Великая пирамида в Гизе Александрийский маяк
