X
Код презентации скопируйте его
Математика и поэзия
Скачать эту презентацию
Презентация на тему Математика и поэзия
Скачать эту презентациюCлайд 1
Руководитель: учитель математики Фабер Галина Николаевна
Cлайд 2
Cлайд 3
Н.И Лобачевский (1792-1856) Омар Хайям (ок.1048 - после 1122)
Cлайд 4
Cлайд 5
Параллельно с занятиями наукой Хайям создавал свои четверостишия (“Рубаи”). Научные труды Хайям писал на арабском языке, стихотворения на персидско-таджикском наречии. Одним из крупнейших математиков, который был замечательным поэтом, является Омар Хайям. Омар Хайям завершил построение геометрической теории кубических уравнений. Математики стран ислама уделяли большое внимание развитию численных методов решения уравнений. Они были необходимы для развития астрономии, которая основывалась не только на наблюдениях, но и на вычислениях с использованием тригонометрических таблиц.
Cлайд 6
Омар Хайям навсегда вошел в историю всемирной культуры не только как блестящий ученый – энциклопедист, но и как прекрасный поэт, который воспевал свободу, бичевал ханжество и лицемерие, высмеивал суеверия. Его мудрые лирические четверостишия, наполненные глубоким философским смыслом в XIX и XX веках, были переведены на все основные языки мира.
Cлайд 7
Cлайд 8
Гениальный русский ученый Михаил Васильевич Ломоносов (1711–1765) является творцом идей новой науки во многих областях. Он величайший химик, физик, геолог и в то же время историк, языковед и даже поэт. Ломоносов был крупнейшим русским поэтом-просветителем 18 в. В России Ломоносов стал создателем оды как жанра философского и высокого гражданского звучания. Свои научные мысли он нередко излагал поэтическим языком. Его философские оды были впоследствии высоко оценены А. С. Пушкиным.
Cлайд 9
Cлайд 10
Ломоносов глубоко понимал значение математики для изучения других наук и для развития ума. Он неоднократно говорил о своих занятиях математикой. Получив поручение написать для обновляемого корпуса учебные программы по физике, химии и математике и обосновать необходимость их изучения, Ломоносов после подробного разговора о значении преподавания кадетам физики и химии, о математике пишет лишь одну фразу: “А математику уже затем учить следует, что она ум в порядок приводит”. В 1755 во многом благодаря усилиям Ломоносова был основан первый в России Московский университет, который ныне носит его имя. А. С. Пушкин сказал о нем: “Ломоносов создал первый русский университет, он, лучше сказать, сам был нашим первым университетом”.
Cлайд 11
Видный представитель символизма в поэзии начала ХХ века В. Я. Брюсов изучал статистические закономерности в произведениях поэзии. Он писал: “Математику как олицетворение рассудочности обычно противопоставляют поэзии, постигающей мир иными, не рассудочными средствами”.
Cлайд 12
Cлайд 13
Один профессор математики недавно просил меня объяснить ему словами мою живопись. Но это ведь то же самое, что просить математика объяснить свои формулы красками на полотне Мы любим всё – и жар холодных чисел, И дар божественных видений, Нам внятно всё – и острый гальский смысл, И сумрачный германский гений.
Cлайд 14
Михаил Юрьевич Лермонтов постоянно искал новой деятельности и никогда не отдавался весь тому высокому поэтическому творчеству, которое обессмертило его имя и которое, казалось, должно было поглотить его всецело. Постоянно меняя занятия, он со свойственной ему страстью, с полным увлечением отдавался новому делу. Известно, что Лермонтов был большим любителем математики и в своих вольных переездах из одного места службы в другое всегда возил с собой учебник математики.
Cлайд 15
Портрет фантастического математика, написанный кистью Лермонтова, после Великой Октябрьской революции поступил Пушкинский Дом Академии наук, где и хранится в настоящее время. Таким образом, он одно время исключительно занимался математикой. Однажды, приехав в Москву к Лопухину, Лермонтов заперся в кабинете и до поздней ночи сидел над решением какой-то математической задачи. Не решив ее, Лермонтов, измученный, заснул. Задачу эту он решил во сне.
Cлайд 16
В наши дни литературные журналы не помещают научных статей на своих страницах, а по заказу Пушкина князь П.Б.Козловский писал математические статьи для его журнала «Современник». В библиотеке Пушкина имелись сочинения по теории вероятностей. Хорошо известно, что Александру Сергеевичу Пушкину математика не давалась с детства и поэтому он её не любил. Кажется, что свидетельств его современников более чем достаточно для того, чтобы сделать вывод о неприязненном отношении Пушкина к математике в течение всей его непродолжительной жизни. На самом деле это неверно.
Cлайд 17
Внимание к теории вероятностей связано по-видимому с тем глубоким интересом, который проявлял Пушкин к проблеме соотношения необходимости и случайности в историческом процессе. Сам А.С.Пушкин был страстным игроком в карты. Возможно, что страсть Пушкина к картам являлась дополнительной причиной его повышенного интереса к этой науке.
Cлайд 18
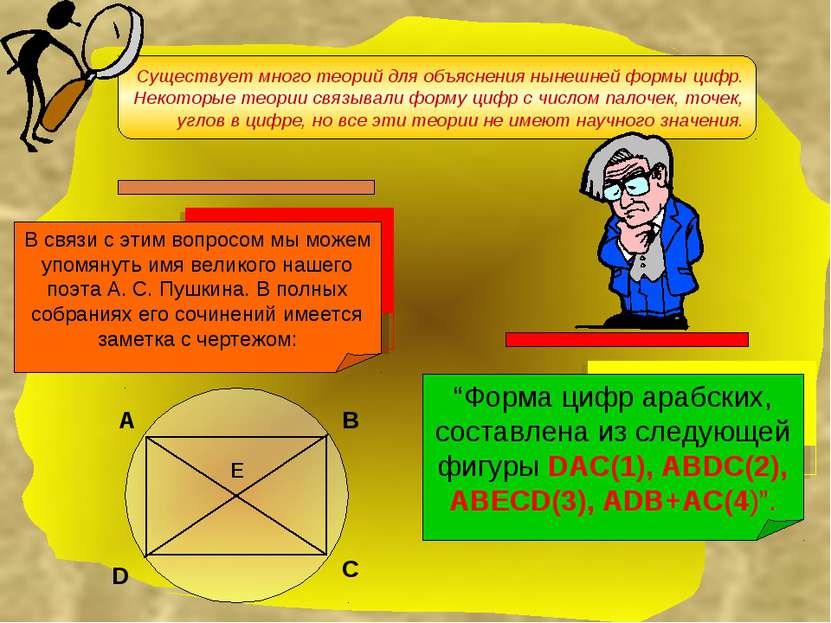
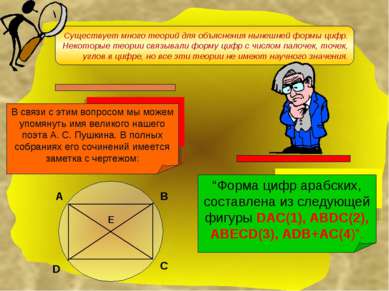Существует много теорий для объяснения нынешней формы цифр. Некоторые теории связывали форму цифр с числом палочек, точек, углов в цифре, но все эти теории не имеют научного значения. А В Е D С
Cлайд 19
Сам он обладал всем этим в высшей степени. И когда он композиционно организовывал свои произведения, он, конечно же, руководствовался этой внутренней «математикой» - безошибочно точным глазомером и непогрешимо верной рукой величайшего мастера-художника: не по заранее подготовленным математическим формулам располагал «части в отношении к целому», но само это расположение оказывалось в полном с ними соответствии, было удивительно математично. А.С.Пушкин считал, что писатель должен иметь «чувство сообразности», обладать «силой ума, располагающего части в отношении к целому».
Cлайд 20
Рассмотрим композицию «Пиковой дамы». В этой повести кульминационным моментом является сцена в спальне у графини, куда проник Герман в надежде узнать тайну трёх карт. В повести (издания 1978 г.) 853 строки. Кульминационный момент повести – это смерть графини. Ему отвечает 535-я строка. Эта строка расположена в повести почти точно в месте золотого сечения, так как 835:535 = 1,6. Совпадение кульминационных моментов в произведениях прозы у А.С.Пушкина удивительно близкое с золотой пропорцией. В заключении осталось выразить надежду на то, что нам удалось в какой-то степени обосновать, на первый взгляд, «странное сближение» Пушкина и математики.
Cлайд 21
На вечерах Великопольского, давнишнего приятеля Пушкина, которого бывали Пушкин и Лобачевский. Встретились два гения. Может быть, после встречи с Николаем Ивановичем Пушкин сказал: “Вдохновение нужно в поэзии, как в геометрии”.
Cлайд 22
Cлайд 23
«Принцесса науки» Крупнейшим литератором и математиком была С. В. Ковалевская. Дядя ее, Петр Васильевич Коровин-Круковский, был умным, начитанным собеседником. Он рассказывал Соне сказки, учил играть в шахматы и между делом незаметно сумел привить ей уважение к математике “… как к науке высшей и таинственной, открывающей перед посвященными в нее новый, чудесный мир”, как писала потом сама С. В. Ковалевская. В 1874 г. Геттингенский университет присудил С. В. Ковалевской степень доктора философии “с высшей похвалой”. Теперь она имела право преподавать математику в высшем учебном заведении.
Cлайд 24
Однако в течение нескольких лет Ковалевская не могла найти применения своим знаниям. Средств к существованию стало мало. Чтобы обеспечить себя, она писала стихи, повести, романы, критические статьи для журналов и газет. За выдающиеся заслуги Русская Академия наук избрала С. В. Ковалевскую своим членом – корреспондентом. Министр просвещения Франции присвоил ей почетное звание “Офицера просвещения”. Этого звания удостаивались лишь некоторые. Вся ее прекрасная жизнь есть образец служения науке. Софья Васильевна Ковалевская говорит о математике так: “Это наука, требующая наиболее фантазии, нельзя быть математиком, не будучи в то же время поэтом в душе”.
Cлайд 25
Cлайд 26
Французский философ, математик, физик и физиолог. Заложил основы аналитической геометрии, дал понятия переменной величины и функции, ввел многие алгебраические обозначения. Он так проявил себя в литературном мастерстве, что занесён в ряд основателей французской прозы нового времени. Вообще-то он и начал свою творческую жизнь с поэзии и много работал в этом жанре. Увековечил он себя в области математики и философии, а всё же его последней работой была пьеса в стихах.
Cлайд 27
Вывод: ВЫВОД: В представлении многих, учёные – полуабстрактные существа, «сухари», погружённые в свою науку и ничем другим не интересующиеся. Однако большое математическое дарование нередко сочетается с проявлением творческого интереса к поэзии. История «великих жизней» даёт тому немало подтверждений. Исследовав лишь немногие из них, становится ясно, что знаменитые математики писали стихи, а великим поэтам была не чужда математика. Математика – точная, абстрактная и строгая наука. Некоторые ошибочно думают - говорила великий русский математик-женщина С. Ковалевская, что математика - это сухая наука. Они смешивают математику с арифметикой, в которой проводятся вычисления, порой трудные и скучные, с числами. Но для того чтобы быть настоящим математиком, добавила С.Ковалевская, нужно быть поэтом в душе.
Cлайд 28
1. Большая энциклопедия «Кирилл и Мефодий »/www.KM.ru/ 1996-2004. 2. Энциклопедия для детей. Математика / Ред. Коллегия: М. Аксёнова, В. Володин – М.: «Аванта +» , 1998. 3. Еженедельная учебно–методическая газета «Математика». Издательский дом «Первое сентября» www.1september/ru 4. « Великие жизни в математике» Б. А. Кодемский . М: « Просвещение» 1995. 5. Сайты Интернета.
