X
Код презентации скопируйте его
История счёта
Скачать эту презентацию
Презентация на тему История счёта
Скачать эту презентациюCлайд 1
История счёта
Cлайд 2
выполняли Масохин Семён г. Москва Куликов Фёдор г. Москва ШКОЛА 531 класс 6 «А»
Cлайд 3
математика ГДЕ МОМЕНТ ПОЯВЛЕНИЯ МАТЕМАТИКИ НА ПЛАНЕТЕ 4000 лет назад в Вавилоне умели решать квадратные уравнения, системы из двух линейных уравнений с двумя неизвестными, а также системы из двух уравнений, одно из которых - квадратичное. Мало того, что умели решать, но еще и применяли для землемерия, для строительного и военного дела. Но самой главной ценностью математики было принято считать ее Евклидову структуру: определения, аксиомы, теоремы. Впервые такая структура явно проявилась в V веке в едином изложении Евклидом всех известных тогда знаний по геометрии, т.е. в синтезе разрозненных знаний в одно целое, в одну науку. Раньше понимали, что главное в труде Эвклида - СИНТЕЗ, индукция. А аксиоматизацию считали только лишь СРЕДСТВОМ выполнить этот синтез. И, поскольку первый синтез математических знаний наблюдается нами в геометрии, потому, наверное, нам и внушали, что началом математики, как науки, следует считать время возникновения геометрии. "Геометрия" = "землемерие". Искусство землемерия было хорошо развито 3000 лет назад в Египте в связи с необходимостью восстанавливать границы посевных участков после весеннего разлива Нила. Именно такой возраст математики нам указывали в школе. Таким образом, если возраст математики приравнять возрасту геометрии, а возраст геометрии считать приближенно равным возрасту Египетского царства, то разброс в определении момента появления математики - сотни лет.
Cлайд 4
БРОНЗОВЫЙ ВЕК В конце XX века историки свели воедино многочисленные данные о Бронзовом веке, и стало ясно, что большие государства, сходные по цивилизации, связанные торговлей и дипломатией, существовали задолго до появления Египетского царства. занимали значительные пространства, сравнимые с территориями империй. Мы очень многого не знаем о той поре Человечества. Кажется, до сих пор не удалось найти даже следов письменности Бронзового века. Однако трудно усомниться в мысли, что государственное управление земледелием и присущее ему землемерие были развиты и тогда. С учетом этого неопределенность в определении начала математики достигла тысяч лет.
Cлайд 5
ТОРГОВЛЯ Некоторые историки склонны считать началом математики момент появления искусства счета. Одно время в истории науки было принято связывать возникновение счета с возникновением торговли. Торговля в той или иной форме характерна даже для отсталых племен. Но некоторые историки утверждают, что счет появился раньше торговли - примерно 35 000 лет назад, в эпоху освоения скотоводства. Жизнь пастушеских племен зависела от численности стад, поэтому им пришлось изобрести и развивать искусство счета. Это, якобы, доказывают некоторые наскальные рисунки древних людей. Неопределенность возросла до десятков тысяч лет.
Cлайд 6
ПЕРВЫЙ СЧЁТ У ЛЮДЕЙ В вопросе уточнения момента возникновения математики среди людей имеется масса обстоятельств, не заметных на первый взгляд. Например: проблема непрерывности наследования знаний потомками. Предположим, в момент t1 некоторое племя A обладало неким Знанием, но потом вымерло. А потом, в момент t2, это же Знание заново открыло другое племя B и передало его своим потомкам, здравствующим до нынешнего дня. Что следует считать моментом возникновения Знания? Очевидно, возможны оба толкования. В случае, когда первое толкование (момент = t1) кажется неприемлемым, возникает вопрос: где гарантия, что племя B в будущем не вымрет? Возникает опасение, что при любом решении мы никогда не можем быть уверены в том, что уточнили все обстоятельства этого вопроса.
Cлайд 7
ЕСТЬ ЛИ СЧЁТ У МОЛЕКУЛ Если уточнить само понятия "счет", то, как мне кажется, может оказаться, что счетом владеют и некоторые микроорганизмы. Я не исключаю, что при некотором толковании понятия "счет" ("сосчитать" означает еще и "запомнить" и "сообщить") вполне может оказаться, что искусством счета владеют и некоторые молекулы. Сами понимаете, тогда счет пойдет на миллиарды лет или даже уйдет в неведомые нам дали, о которых только физики имеют смелость что-то утверждать.
Cлайд 8
ВЛАДЕЮТ ЛИ АРИФМЕТИКОЙ МУРАВЬИ Нет оснований считать людей первыми на планете изобретателями счета. Некоторые виды муравьев умеют считать и сообщать числовую информацию друг другу. Было два типа опытов. В опытах первого типа использовали лабиринт в виде двоичного дерева, муравья - разведчика и муравьев - фуражиров. Разведчик проходил путь от корма до дома. Дома фуражиры получали от разведчика информацию о месте нахождения корма. Время разговора разведчика с фуражирами измеряли. Затем разведчика изолировали от фуражиров и заменяли экземпляр лабиринта (сохраняя структуру и место нахождения корма) - чтобы устранить возможность фуражирам идти по следам разведчика. После чего фуражиров запускали из дома в лабиринт. Последовательность поворотов в узлах лабиринта по дороге к корму исследователи кодировали последовательностью единиц и нулей. Засекали время прохождения фуражирами от начала лабиринта до корма. Потом обрабатывали наблюдения статистически, стремясь найти зависимость между временем разговора и сложностью информации о пути (в виде последовательности нулей и единиц). Таким способом исследователи хотели оценить объем информации, которую муравьи могут передать друг другу. У них получилось - несколько бит как минимум.
Cлайд 9
троя
Cлайд 10
Город троя Известно ,что в городе Троя жили 3 великих математика Архимед, Пифагор, Эвклид именно поэтому город Троя считают городом откуда пошла математика.
Cлайд 11
История возникновения моделирования. Исторически первыми моделями как заместителями некоторых объектов были, языковые знаки, возникшие в ходе развития человечества и постепенно превратившиеся в разговорный язык. Слово было первой моделью реального объекта. Следующим этапом развития моделирования можно считать возникновение знаковых числовых обозначений. Сведения о результатах счета первоначально сохранялись в виде зарубок. Постепенное совершенствование этого метода привело к изображению чисел в виде цифр как системы знаков. Можно предположить, что именно зарубки были прототипом римских цифр.Значительное развитие моделирование получило в древней Греции. В V-III веках до нашей эры в Греции была создана геометрическая модель Солнечной системы. Греческий врач Гиппократ для изучения человеческого глаза воспользовался его физической моделью - глазом быка. В основе термина "модель" лежит латинское слово modulus - мера, образец. Появление этого термина было обусловлено тем обстоятельством, что при изучении сложных явлений, процессов, объектов, устройств или систем (обобщенно-объектов исследования) не всегда удается учесть полную совокупность факторов, определяющих свойства объекта исследования.
Cлайд 12
17век – первый шаг в современной науке. Принято считать, что современная наука начала формироваться в 17 веке. Природа говорит с нами на языке математики – заявил около 1630 года Галилей. Мы знаем понятия такие как арифметика, геометрия, алгебра или математический анализ, но не всегда чувствуем их единство. От того наше представление о законах природы не полно, и нередко оно противоречиво. И противоречие требует перестройки в системе математических понятий. Что-то привычное мы вынуждены отвергнуть, как заблуждение; другие знакомые слова приобретают новый смысл. Галилео Галилей
Cлайд 13
Не удивительно, что у истока новой науки собрались люди с причудливыми характерами. Всех их объединяло безграничное любопытство, беспредельное трудолюбие и буйная фантазия. Первым в этом ряду оказался немец Иоганн Кеплер (1571-1630) - неутомимый наблюдатель и неугомонный вычислитель. Он вошел в большую науку в 1600 году, наблюдая за движением планет среди звезд в течение 30 лет в Пражской обсерватории. Привёл накопленные данные в единую систему, отвергнув модели Птолемея и Коперника. Кеплер научился вычислять путь, пройденный планетой за данное время, по известной скорости планеты. Коперник Иоганн Кеплер Птолемей Выдающийся учёный 17 века, оспоривший учения Птолемея и Коперника .
Cлайд 14
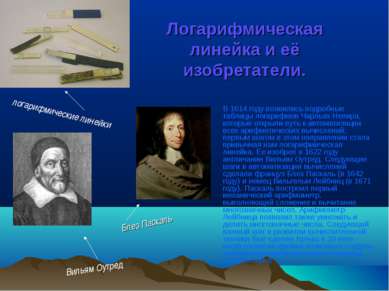Логарифмическая линейка и её изобретатели. В 1614 году появились подробные таблицы логарифмов Чарльза Непира, которые открыли путь к автоматизации всех арифметических вычислений; первым шагом в этом направлении стала привычная нам логарифмическая линейка. Ее изобрел в 1622 году англичанин Вильям Оутред. Следующие шаги в автоматизации вычислений сделали француз Блез Паскаль (в 1642 году) и немец Вильгельм Лейбниц (в 1671 году). Паскаль построил первый механический арифмометр, выполняющий сложение и вычитание многозначных чисел. Арифмометр Лейбница позволил также умножать и делить многозначные числа. Следующий важный шаг в развитии вычислительной техники был сделан только в 20 веке - когда развитие физики позволило создать электронные вычислительные машины (компьютеры) Вильям Оутред логарифмические линейки Блез Паскаль
Cлайд 15
Французский учёный, открывший координаты. Революцию произвел в 1637 году другой великий математик - француз Рене Декарт (1596-1650). В отличие от Кеплера, Декарт не любил долгих расчетов. Он предпочитал наглядно-геометрические рассуждения и хотел работать этим методом с любыми сложными кривыми. Он заметил, что многие кривые на плоскости задаются простыми уравнениями, и ввёл на плоскости координаты, изобразив каждую точку парой чисел (х, у). Рене Декарт y x 0 .А
Cлайд 16
Большой вклад в развитие математики внёс Пьер Ферма из Тулузы (1601-1665). По основной профессии он был юрист, а математикой занимался на досуге - читая книги классиков или современников и размышляя о тех задачах, которые другие не заметили или не сумели решить. Понятно, что при таком способе работы Ферма ни в одной области науки не был первым. Он добавлял в уже готовую или только рождающуюся науку столь важные открытия, что превзойти его результаты могли только гении - порою много десятилетий спустя. В целом, деятельность Ферма можно сравнить с работой полноценной академии наук. Но - при жизни Ферма таких академий еще не было!
Cлайд 17
Как в 17 веке учёные узнавали об открытиях своих дальних коллег. Не было и научных журналов для публикации новых открытий. Поэтому все крупные ученые Европы узнавали о новых достижениях своих коллег из взаимной переписки. Некоторые любители математики сделали такую переписку своим главным вкладом в науку. Они регулярно сообщали всем своим корреспондентам о том, какие факты открыли их далекие коллеги. Как только их стало больше - общую работу пришлось организовать с помощью научных учреждений. Этот перелом произошел в 1660-е годы. В 1662 году объявило о своем рождении Королевское Общество в Лондоне, а в 1666 году по его образцу возникла Парижская Академия Наук. Оба эти содружества ученых сразу начали публиковать отчеты о своих собраниях и о тех открытиях, которые там обсуждались. Парижская академия наук
Cлайд 18
Великий учёный 18 века. XVIII век в математике можно кратко охарактеризовать как век анализа, который стал главным объектом приложения усилий математиков. Лидером математиков XVIII века был Леонард Эйлер, чей исключительный талант наложил отпечаток на все основные математические достижения столетия. Эйлер продвинул практически все области математики. В алгебре назревают новые идеи, завершившиеся уже в XIX веке. В геометрии появляются новые разделы… Леонард Эйлер
Cлайд 19
Центрами математических исследований становятся Академии наук, по большей части государственные. Значение университетов невелико, физико-математические факультеты всё ещё отсутствуют. Ведущую роль играет Парижская академия. Английская школа после Ньютона обособляется и на целый век снижает научный уровень; Математики становятся профессионалами, любители почти исчезают со сцены. В конце XVIII века появляются специализированные математические журналы, увеличивается интерес к истории науки. Выходит двухтомная «История математики» Монтюкла расширяется издание научно-популярной литературы.
Cлайд 20
Рост математики в 19 веке В XIX веке возникает и получает широкое развитие математическая логика, этот век становиться веком геометрии. В целом в XIX веке роль и престиж математики в науке и экономике заметно растут. Соответственно растёт и её государственная поддержка. Появляются первые математические общества: Лондонское, Американское, Французское, Московское, а также общества в Палермо и Эдинбурге. Крупнейшим достижением стало введение понятие вектора, которое ввёл У. Гамильтон. У. Гамильтон
Cлайд 21
Николай Иванович Лобачевский Во второй половине XIX века наконец привлекает общее внимание геометрия Лобачевского. В своей первой работе «О началах Геометрии» он критически пересмотрел геометрические понятия со времён Евклида (3-ий век до н.э.) . Лобачевский настолько опередил своё время, что был оценён по заслугам только спустя много лет после смерти. Несколько важных открытий общего характера сделала Софья Ковалевская. Софья Ковалевская
Cлайд 22
Во второй половине XIX века российская математика публикует и немало фундаментальных результатов Пафнутия Львовича Чебышёва, Андрея Андреевича Маркова .К концу XIX века формируются две активные отечественные математические школы — московская и петербургская. Андрея Андреевича Маркова Пафнутия Львовича Чебышёва
Cлайд 23
Учёные- математики 20-ого века Престиж профессии математика стал в XX столетии заметно выше. Математика развивалась, и невозможно сколько-нибудь полно перечислить сделанные открытия. В них принимали участие такие видные учёные как Давид Гильберт, Герман Минковский. А. Н. Колмогоров, Норберт Винер и др. Давид Гильберт А. Н. Колмогоров
Cлайд 24
Особенное развитие в XX веке получили новые области математики связанные с компьютерными потребностями. Слово 'компьютер' означает 'вычислитель', т.е. устройство для вычислений. Многие тысячи лет назад для счета использовались счетные палочки, камешки и т.д. Более 1500 лет тому назад (а может быть и значительно раньше) для облегчения вычислений стали использоваться счеты. Первая настоящая счетная машина появилась лишь в 1642г. Её изобрел французский математик Паскаль. Построенная на основе зубчатых колёс, она могла суммировать десятичные числа. В 1673г. немецкий математик Лейбниц изобрел машину, которая выполняла все четыре арифметические действия. Она стала прототипом арифмометров, использовавшихся с 1820г. до 60-х годов ХХ века. Начиная с XIX в. арифмометры получили очень широкое применение. На них выполняли даже очень сложные расчеты, например, расчеты баллистических таблиц для артиллерийских стрельб. Но многие расчеты производились очень медленно и запись результатов производились человеком, а скорость его работы весьма ограничена. арифмометр
Cлайд 25
Продолжение К началу XX века времени потребность в автоматизации вычислений, особенно для военных нужд - баллистики, криптографии стала настолько велика, что над созданием машин типа построенных Эйкеном и Цузе одновременно работало несколько групп исследователей. Во второй половине 40-х годов появились первые электронно-вычислительные машины, элементной базой которых были электронные лампы. В 1943 г. группа американских специалистов под руководством Джона Мочли и Преспера Экерта начала конструировать подобную машину уже на основе электронных ламп, а не реле. Их машина, названная ENIAC, работала в тысячу раз быстрее, чем Марк-1, однако для задания ее программы приходилось в течение нескольких часов или даже нескольких дней подсоединять нужным образом провода. Для упрощения процесса задания программ, Мочли и Экерт стали конструировать новую машину, которая могла бы хранить программу в своей памяти. В 1945 г. к работе был привлечен знаменитый математик Джон фон Нейман, который подготовил доклад об этой машине. В 1945 г. знаменитый немецкий математик Джон фон Нейман ясно и просто сформулировал в своём докладе общие принципы функционирования компьютеров. С той поры компьютеры стали гораздо более мощными, но они соответствуют тем принципам, которые изложил он в своём докладе. С появлением в 80-х годах первых персональных компьютеров, темпы развития резко возросли деятельности. В настоящее время нет ни одной сферы, где не использовались компьютеры. Одна из первых электронно-вычислительных машин.
