X
Код презентации скопируйте его
По страницам истории математики
Скачать эту презентацию
Презентация на тему По страницам истории математики
Скачать эту презентациюCлайд 1
По страницам истории математики «Не зная прошлого, трудно понять настоящее…»
Cлайд 2
Матричная система мер 200 лет назад в различных странах, в том числе и России, применялись различные системы единиц для измерения длины, массы и других величин. Соотношение между мерами были сложны, существовали разные определения для единиц измерения. Например, и до сих пор в Великобритании существуют две различные «тонны» - в 2000 и в 2940 фунтов, более 50 различных «бушелей» и т. п. Это затрудняло развитие науки, торговли между странами. Поэтому назрела необходимость введения единой системой мер, удобной для всех стран, с простыми соотношениями между единицами. Такая система – её называли матричной системы мер – была разработана во Франции. Основную единицу длины 1 метр (от греческого слова «метрон» - мера) определили как сорокамиллионную долю окружности Земли, основную единицу массы 1 кг – как массы 1 дм3 чистой воды. Остальные единицы определялись через эти две, соотношения между единицами одной величины равнялись 10, 100, 1000 и т. д.
Cлайд 3
Великие математики Метрическая система мер принята большинством стран мира. В России её введение началось с 1899 года, но только после Октябрьской революции она стала обязательной. Большие заслуги во введении и распространении метрической системы мер в нашей стране принадлежат Дмитрию Ивановиче Менделееву, великому русскому химику.
Cлайд 4
Старые единицы измерения По традиции и в настоящее время иногда пользуются старыми единицами. Моряки расстояния измеряют милями (1852 м) и кабельтовыми (десятая часть мили, то есть около 185 м), скорость – узлами (1 миля в час). Массу алмазов – измеряют в каратах (200 мг, то есть пятая часть грамма – масса пшеничного зерна). Объём нефти измеряют в баррелях (159 л) и т.д.
Cлайд 5
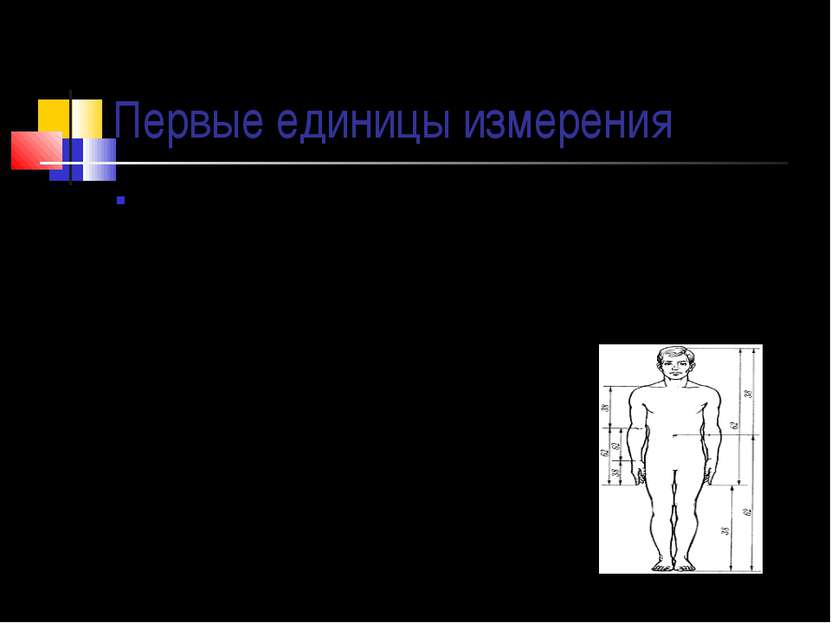
Первые единицы измерения Первые единицы длины как в России, так и в других странах были связаны с размерами частей тела человека. Таковы сажень, локоть, пяди. В Англии и США до сих пор используется «ступня» - фут (31 см), 2 -большой палец» - дюйм (25 мм) и даже ярд (91 см) – единица длины, появившаяся почти 900 лет назад. Она была равна расстоянию от кончика носа короля Генриха I до конца пальцев его вытянутой руки.
Cлайд 6
Единицы измерения в Древней Руси В Древней Руси в качестве единиц измерения длины применялись: косая сажень (248 см) – расстояние от пальцев левой ноги до конца пальцев поднятой правой руки, маховая сажень (176 см) - расстояние между концами пальцев расставленных в стороны рук, локоть (45 см) – расстояние от концов пальцев до локтя согнутой руки.
Cлайд 7
Русские меры Для измерения больших расстояний на Руси использовали единицу «попроще», заменённую позже верстой (в разных местностях версту считали по–разному – от 500 до 750 сажен). От восточных купцов пошла единица «аршин» (тоже означает «локоть») – существовали турецкий аршин, персидский аршин и др. Поэтому и возникла поговорка «мерить на свой аршин». Множество единиц существовало и для измерения массы. Наиболее древняя русская мера – «гривна», или «гривёнка» (около 410 г), позднее появились золотники, фунты, пуды. В связи с развитием торговли назрела необходимость установить чёткие определения единиц и соотношений между ними. При Петре I русские меры были приведены в определенную систему:
Cлайд 8
Перевод одних единиц измерения в другие 1 верста = 500 сажен (1 км 65 м); 1 сажень = 3 аршинам (213 см); 1 аршин = 16 вершкам = 28 дюймам (71 см); 1 фут = 12 дюймам (30 см 5 мм); 1 пуд = 40 фунтам (гривёнкам) (16 кг 400 г); 1 фут = 96 золотникам (410 г).
Cлайд 9
Великие математики Немецкого учёного Карла Гаусса называли королём математиков. Его математическое дарование проявилось уже в детстве. Рассказывают, что в трёхлетнем возрасте он удивил окружающих. Однажды в школе (Гауссу в то время было 10 лет) учитель предложил классу сложить все числа от 1 до 100. Пока он диктовал задание, у Гаусса уже был готов ответ. На его грифельной доске было написано: 101*50=5050. Попробуй догадаться, как Карл Гаусс складывал числа от 1 до 100.
Cлайд 10
Обозначение чисел в Древней Руси Не мало различных способов записи чисел было создано людьми. В Древней Руси числа обозначали буквами с особым знаком « ~ » (титло), который писали над буквой. Первые девять букв – десятки, а последние девять букв – сотни. Число десять тысяч называли словом «тьма» (и теперь мы говорим: «народу тьма тьмущая»). Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли её у индусов. Поэтому цифры, которыми мы сейчас пользуемся, европейцы называют «арабскими», а а арабы – «индийскими». Эта система была введена в Европе примерно в 1120 году английским учёным – путешественником Аделардом К 1600 году она была принята в большинстве стран мира.
Cлайд 11
Русские называния чисел Русские называния чисел тесно связаны с десятичной системой счисления. Например, семнадцать означает «семь на десять», семьдесят – 2семь десяткой», а семьсот – «семь сотен». До сих пор используются и римские цифры, которые употреблялись в Древнем Риме уже около 2500 лет тому назад. I–1, V-5, X-10, L-50, C-100, D-500, M-1000. Остальные числа записываются этими цифрами с применение сложения и вычитания. Так, например, число XXVII означает 27, так как 10+10+5+1+1=27. если меньшая по значению цифра (I, X, C) стоит перед большой, то её значение вычитается. Например, VC означает 4(5-1=4), число MCMLXXXIX означает 1989. В настоящее время римские цифра обычно применяются при нумерации глав и разделов книги, месяцев года, для обозначения дат значительных событий, годовщин.
Cлайд 12
Это интересно Для вычисления запись чисел с помощью римских цифр неудобна. В этом вы можете убедиться сами, если попробуете выполнить, например, сложение чисел ССХVII и XLIX или деление числа CCXCVII на число IX.
Cлайд 13
Старые русские меры массы В старину в России применялись другие меры массы, чем в настоящее время. Так, для взвешивания мелких, но дорогих товаров применялся золотник (около 4 г). В торговле использовались фунт (1 фунт = 96 золотниками), пуд (1 пуд = 40 фунтами), берковец (1 берковец = 10 пудам). Составьте задачу с использованием старых русских мер массы.
Cлайд 14
Измерение площади и объема на Руси Во многих западных странах использовалась единица площади акр. Акр примерно равен 4047 м2. Сравните 1 акр и 1 га. На Руси в старину использовались в качестве единиц измерения объёма ведро (около 12 л), штор (десятичная часть ведра). В США, Англии и других странах используются баррель (около 159 л), галлон (около 4 л), бушель ( около 36 л), пинта (от 470 до 568 кубических сантиметров). Сравните это единицы. Какие из них больше 1 м3?
Cлайд 15
Время В старину часто пользовались солнечными часами, они известны более 200 лет. В солнечных часах время определяется по положению тени от наклонного стержня на циферблате (циферблат располагали так, чтобы в полдень тень была направлена на север). Подумайте, что общего у этих часов с современными, в чём их достоинства и недостатки.
Cлайд 16
Деньги на Руси В старину на Руси использовались монеты достоинством меньше одной копейки: грош – ½ к. и полушка – ¼ к. Другие монеты тоже имели названия: 3 к. – алтын, 5 к. – пятак, 15 к. – пятиалтынный, 10 к. – гривенник, 20 к. – двугривенный, 25 к. – четвертак, 50 к. – полтинник. Подумайте, сколько полушек в алтыне. Сколько грошей в пятаке? Как гривенник можно разменять на алтыны и гроши? Сколько сдачи с пятиалтынного надо получить при покупке стоимостью в гривенник и три гроша? Сколько пятаков в четвертаке? Почему 25 к. назвали четвертаком, а 50 к. – полтинником?
Cлайд 17
Как появились дроби С древних времён людям приходилось не только считать предметы (для чего требовалось натуральные числа), но и измерять длину, время, площади, весть расчёты за купленные или проданные товары. Не всегда результаты измерения или стоимость товара удавалось выразить натуральные числа. Приходилось учитывать и части, доли меры. Так появились дроби. В русском языке слово «дробь» появилось в VIII веке, оно происходит от глагола « дробить» - разбивать, ломать на часть. В первых учебниках математики (в XVII веке) дроби так и назывались – «ломаные числа». У других народов название дроби также связанно с глаголами «ломать», «разбирать», «раздроблять».
Cлайд 18
Названия дробей В старинных книгах можно встретить такие названия дробей; 1/2 – пол, полтина, 1/5 – пятина, 1/7 – седьмина, 1/10 – десятина. Подумайте, как появились следующие названия: 1/4 - четь, 1/8 – полчети, 1/16 – полполчети, 1/32 – полполполчети (малая четь) . Дробь 1/3 называли «треть». Попробуйте догадаться, как называли дроби 1/6, 1/12, 1/24. Подумайте, почему смешанные числа называли: 1 ½ - полвтора, 2 ½ - полтретья, 3 ½ - полчетверта, 4 ½ - полпяты, 5 ½ - полшесты и т.д. Сохранился ли такой способ чтения в наше время?
Cлайд 19
Великие математики Современное обозначение дробей берёт своё начало в Древней Индии; его стали использовать и арабы, а от них в XII – XIV веках оно было заимствовано европейцами. Вначале в записи дробей не использовалась дробная черта; например, числа 1/5, 2 1/3 записывались так: 1 5, 2 1 3. Черта дроби стала постоянно использоваться лишь около 300 лет назад. Первым европейском учёным, который стал использовать и распространять современную запись дробей, был итальянский купец и путешественник , сын городского писаря Фибоначчи (Леонардо Пизанский) в 1202 г. Он ввёл слово «дробь». Название «численность» и «знаменатель» ввёл в XII веке Максим Плануд – греческий монах, учёный – математик.
Cлайд 20
Десятичные дроби В науке и промышленности, в сельском хозяйстве десятичный дроби используются значительно чаще, чаще, чем обыкновенные. Это связано с простотой правил вычислений с десятичными дробями, похожестью их на правила действий с натуральными числами. Правила вычислений с десятичными дробями описал знаменитый учёный средневековья аль - Каши Джемшид Ибн Масуд, работавший в городе Самарканде в обсерватории Улугбека в начале XV века. Записывал аль – Каши десятичные дроби так же, как принято сейчас, но записывал красными чернилами или отделял вертикальной чертой.
Cлайд 21
Великие математики В России учение о десятичных дробях изложил Леонтий Филиппович Магницкий в 1703 году в первом учебнике математики «Арифметика, сиречь наука числительная».
Cлайд 22
Первые вычислительные устройства Первыми «вычислительными устройствами», которыми пользовались в древности люди, были пальцы рук и камешки. Позднее появились бирки с зарубками и верёвки с узелками. В Древнем Египте и Древней Греции задолго нашей эры использовали абак - доску с полосками, по которым передвигались камешки. Это было первое устройство, специально предназначенное для вычислений. Со временем абак совершенствовали – в римском абаке камешки или шарики передвигались по желобкам ( от римлян к нам перешло слово «калькуляция», означающее буквально «счёт камешками») ; в китайских счётах «суан – пан» и японских «соробан» шарики были нанизаны на прутики. Абак просуществовал до XVII века, когда его заменили письменные вычисления. Русский абак – счёты появились в XVI веке, ими пользуются и в наши дни.
Cлайд 23
Абак Со временем абак совершенствовали – в римском абаке камешки или шарики передвигались по желобкам ( от римлян к нам перешло слово «калькуляция», означающее буквально «счёт камешками») ; в китайских счётах «суан – пан» и японских «соробан» шарики были нанизаны на прутики. Абак просуществовал до XVII века, когда его заменили письменные вычисления. Русский абак – счёты появились в XVI веке, ими пользуются и в наши дни. Большое преимущество русских считов в том, сто они основаны на десятичной системе счисления, а не на пятиричной, как все остальные абаки.
Cлайд 24
Арифмометр и Великие математики Первый арифмометр, выполнявший все четыре арифметических действия, создал в 1673 г. Немецкий физик, изобретатель и математик Готфрид Вильгельм Лейбниц. Наиболее совершенными для того времени арифмометр изобрёл в 1878 году великий русский математик Пафнутий Львович Чебышёв. Вильгельм Лейбниц. Чебышёв.
Cлайд 25
ЭВМ Создание миниатюрных ЭВМ – микрокалькуляторов стало возможно после того, как были разработаны способы изготовления электронных схем, содержащих тысячи транзисторов и других элементов на пластинке размером с ноготь человека. С использованием микрокалькуляторов для вычислений мы и познакомимся в следующем пункте учебника.
Cлайд 26
Проценты Слово «процент» происходит от латинских слов pro centum, что буквально означает «со ста». Проценты дают возможность легко сравнивать между собой части целого, упрощают расчёты и поэтому очень распространены. Широко начали использовать проценты в Древнем Риме но идея процентов возникла много раньше – вавилонские расфасовщики уже умели находить проценты (но они считали не «со ста», а «с шестидесяти», так как в Вавилоне пользовались шестидесятеричными дробями).
Cлайд 27
Обозначение процентов Знак % произошел, как предполагают, благодаря опечатке. В рукописях pro centum часто заменяли словом «cento» - сто и писали его сокращенно – cto. В 1685 году в Париже была напечатана книга по коммерческой арифметике, где по ошибке наборщик вместо cto набрал %. После этой ошибки многие математики также стали употреблять знак % для обозначения процентов, и постепенно он получил всеобщее признание.
Cлайд 28
Промилле Иногда применяют и более мелкие доли целого – тысячные, то есть десятые части процента. Их называют промилле (от латинского «с тысячи») и обозначают %0.
Cлайд 29
Измерение углов Слово «градус» - латинское, означает «шаг», «ступень». Измерение углов в градусах появилось более 3 тыс. лет назад в Вавилоне. В расчётах там использовалась шестидесятеричная система счисления, шестидесятеричные дроби. С этим связано, что полный оборот (окружность) вавилонские математики и астрономы, а в след за ними греческие и индийские делили на 360 частей – градусов (шесть раз по шестьдесят) , каждый градус- на 60 минут, а минуту на 60 секунд:
Cлайд 30
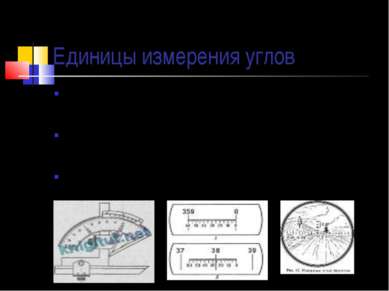Единицы измерения углов В конце XVIII при разработке метрической системы мер французские ученые предложили делить прямой угол не на 90, а на 100 частей. Такой угол в 1/100 прямого угла называют «град»: В градах измеряют углы в геодезии, пользуются в некоторых строительных расчетах, но широкого распространения эта единица не получила. Для точного измерения углов созданы различные инструменты. Основная часть этих приборов – шкала, похожая на шкалу транспортира.
Cлайд 31
Геометрия древности Вы научились измерять длины отрезков и величины углов, площади некоторых многоугольников и объемы прямоугольных параллелепипедов. Все эти фигуры называются геометрическими. С геометрическими фигурами имели дело с глубокой древности и крестьяне и ремесленники, и строители храмов, дворцов и пирамид. Надо было уметь измерять площади земельных участков, подсчитывать объем корзин, которыми собирался урожай, определять, сколько камня потребуется для здания. А чтобы здание не рушилось, стены надо было возводить под прямым углом к поверхности земли. Астрономам древности необходимо было измерять углы для определения положения небесных светил.
Cлайд 32
Из истории Египта Особенно быстро знания о свойствах фигур развивались в Древнем Египте. В этом государстве все земледелие было сосредоточенно на очень узкой полосе земли- в долине реки. Нил. Земли было мало, за участок крестьянин ежегодно платил соответствующий налог фараону. Каждую весну Нил разливался и удобрят землю плодородным илом. Но при разливе смывались границы участков, менялись их площади. Тогда пострадавшие обращались к фараону, а фараон посылал землемеров, чтобы восстановить границы участков, выяснить, как изменилась их площадь, и установить размер налога .
Cлайд 33
Из истории Египта Развивалось в Древнем Египте и строительное искусство, торговля. Знания постепенно накапливались, систематизировались. Около 4 тыс. лет назад возникла наука об измерении расстояний, площадей и объемов, о свойствах различных фигур. Так как в основном речь шла о земельных участках, то древние греки, узнавшие об этой науке от египтян, назвали её геометрией (по-гречески «гео»- земля, а «метрео»- измеряю, значит «геометрия» буквально означает «землемерие»). Греческие ученые узнали много новых свойств геометрических фигур, и уже тогда геометрией стали называть науку о геометрических фигурах, а для науки об измерении Земли ввели другое название - «геодезия» (происходит от греческих слов «деление земли»).
Cлайд 34
Запомните !!! Что бы изучение математики было успешным, что бы учиться было интересно, нужно быть внимательным и сообразительным, уметь хорошо и быстро запоминать, обладать сильной волей, делать наблюдения и выводы, расширяющие круг математических знаний и представлений. Это качество можно развить. В этом вам помогут специальные игры и упражнения.
