X
Код презентации скопируйте его
Моделирование зависимостей между величинами (11 класс)
Скачать эту презентацию
Презентация на тему Моделирование зависимостей между величинами (11 класс)
Скачать эту презентациюCлайд 1
МОДЕЛИРОВАНИЕ ЗАВИСИМОСТЕЙ МЕЖДУ ВЕЛИЧИНАМИ Урок № 25 ТЕХНОЛОГИИ ИНФОРМАЦИОННОГО МОДЕЛИРОВАНИЯ Презентацию подготовила: Некруткина Е.В. учитель информатики и ИКТ МОУ СШ № 32 Волгограда
Cлайд 2
Величина Характеристики величины: имя, тип, значение Функциональные и иные виды зависимостей Математические модели Табличные и графические модели Динамические модели Ключевые понятия
Cлайд 3
Применение математического моделирования Примеры зависимостей: время падения тела на землю зависит от его первоначальной высоты; давление газа в баллоне зависит от его температуры; уровень заболеваемости жителей города бронхиальной астмой зависит от концентрации вредных примесей в городском воздухе. Применение математического моделирования постоянно требует учета зависимостей одних величин от других.
Cлайд 4
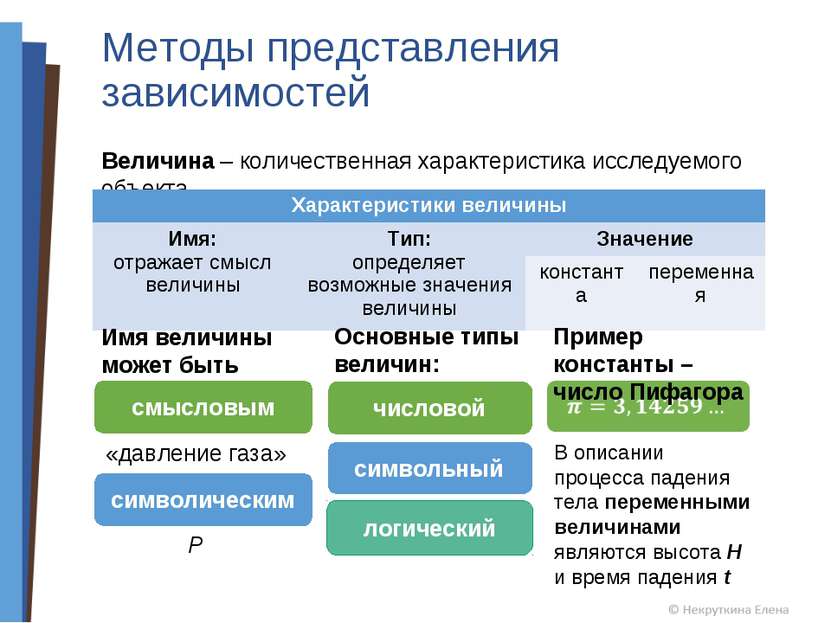
Методы представления зависимостей Величина – количественная характеристика исследуемого объекта Имя величины может быть смысловым символическим «давление газа» Р Основные типы величин: числовой символьный логический Пример константы – число Пифагора В описании процесса падения тела переменными величинами являются высота H и время падения t смысловым Характеристики величины Имя: отражает смысл величины Тип: определяет возможные значения величины Значение константа переменная
Cлайд 5
Виды зависимостей Функциональной зависимостью называется связь между двумя величинами, при которой изменение одной из них вызывает изменение другой. Пример 1: t (c) – время падения; H (m) – высота падения. Зависимость будем представлять, пренебрегая учетом сопротивления воздуха; ускорение свободного падения g (м/с2) будем считать константой. Пример 2: P (н/м2) – давление газа (в единицах системы СИ давление измеряется в ньютонах на квадратный метр); t °C – температура газа. Давление при нуле градусов P0 будем считать константой для данного газа.
Cлайд 6
Виды зависимостей Иная зависимость носит более сложный характер, одна и та же величина может принять разные значения, поскольку на нее могут оказывать влияния и другие показатели. Пример 3: Загрязненность воздуха характеризуется концентрацией примесей – С (мг/м3). Единица измерения – массы примесей, содержится в 1 кубическом метре воздуха, выраженная в миллиграммах. Уровень заболеваемости будет характеризовать числом хронических больных астмой, приходящихся на 1000 жителей данного города P (бол./тыс.)
Cлайд 7
Математические модели Математические модели — это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними, представленных на языке математики. Математические модели отражают физические законы и представляются в виде формул: Корневая зависимость (время пропорционально квадратному корню высоты) Линейная зависимость
Cлайд 8
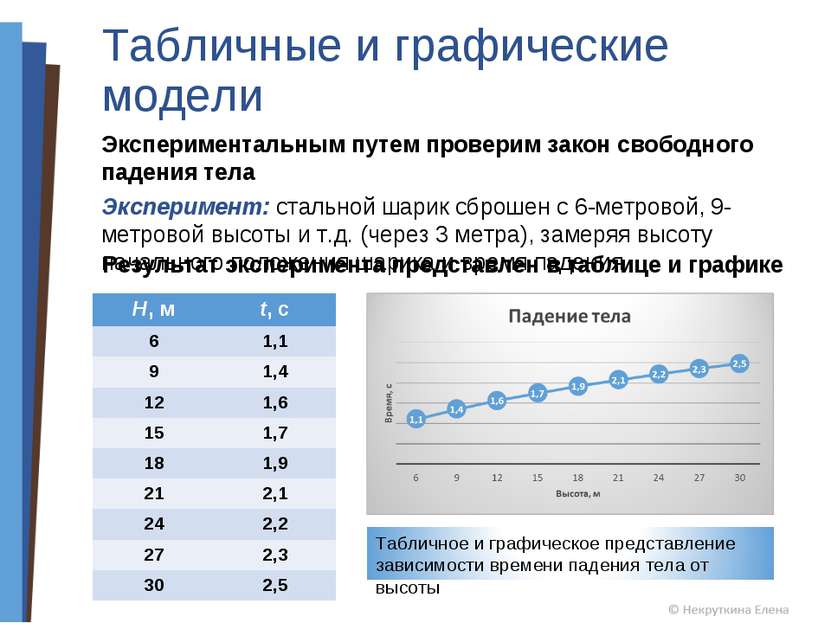
Табличные и графические модели Экспериментальным путем проверим закон свободного падения тела Эксперимент: стальной шарик сброшен с 6-метровой, 9-метровой высоты и т.д. (через 3 метра), замеряя высоту начального положения шарика и время падения Результат эксперимента представлен в таблице и графике Н, м t, c 6 1,1 9 1,4 12 1,6 15 1,7 18 1,9 21 2,1 24 2,2 27 2,3 30 2,5
Cлайд 9
Динамические модели Информационные модели, которые описывают развитие систем во времени, имеют специальное название: динамические модели. В физике это движение тел, в биологии – развитие организмов или популяций животных, в химии – протекание химических реакций.
Cлайд 10
Самое основное Величина – количественная характеристика исследуемого объекта. Характеристики величины: Имя – отражает смысл величины Тип – определяет возможные значения величин Значение: постоянная величина (константа) или переменная Функциональной зависимостью называется связь между двумя величинами, при которой изменение одной из них вызывает изменение другой. Существует три способа моделирования величин: функциональный (формула), табличный и графический Формула более универсальна; имея формулу, можно легко создать таблицу и построить график. Описание развития систем во времени – динамическая модель.
Cлайд 11
Вопросы и задания Какие вам известны формы представления зависимостей между величинами? Что такое математическая модель? Может ли математическая модель включать в себя только константы? Приведите пример известной вам функциональной зависимости (формулы) между характеристиками какого-то объекта или процесса. Обоснуйте преимущества и недостатки каждой из трех форм представления зависимостей. Представьте математическую модель зависимости давления газа от температуры в виде табличной и графической модели, если известно, что при температуре 27 °С давление газа в закрытом сосуде было 75 кПа.
Cлайд 12
Информатика и ИКТ. Базовый уровень : учебник для 10-11 классов / И.Г. Семакин, Е.К. Хеннер. – 7-е изд. – М. : Бином. Лаборатория знаний, 2011. – 246. : ил. Иллюстрации: http://1.bp.blogspot.com/-u7m70qcqIdw/Ukh9R4Ga-9I/AAAAAAAAEkk/wIqkfCqOgGo/s1600/%25D0%2593%25D0%25B0%25D0%25BB%25D0%25B8%25D0%25BB%25D0%25B5%25D0%25BE.gif http://ehsdailyadvisor.blr.com/wpcontent/uploads/2015/11/EHSDA_110615.jpg http://himki.blizhe.ru/userfiles/Image/MIL-GRAFIK/dop-photo/PRIMESI.JPG http://f.10-bal.ru/pars_docs/refs/12/11350/11350_html_mbb50c21.jpg Источники
