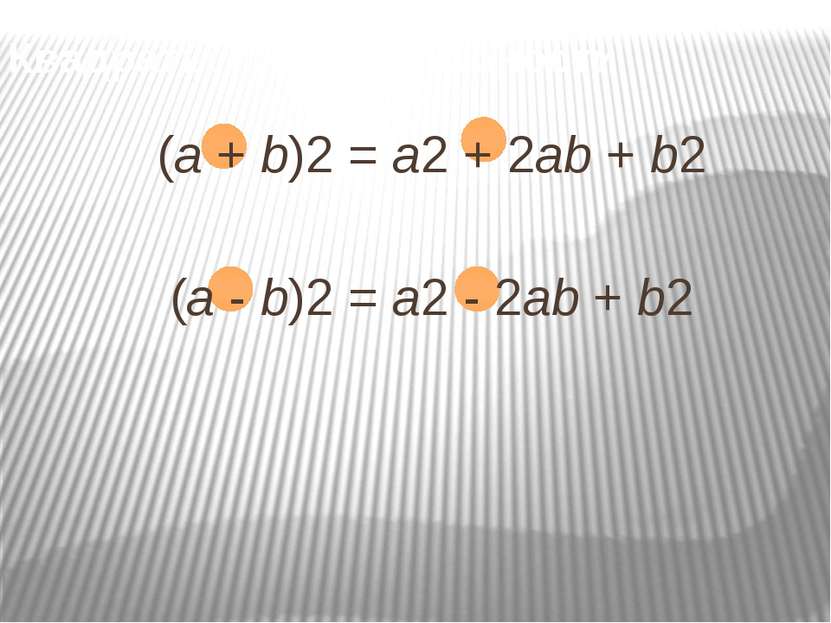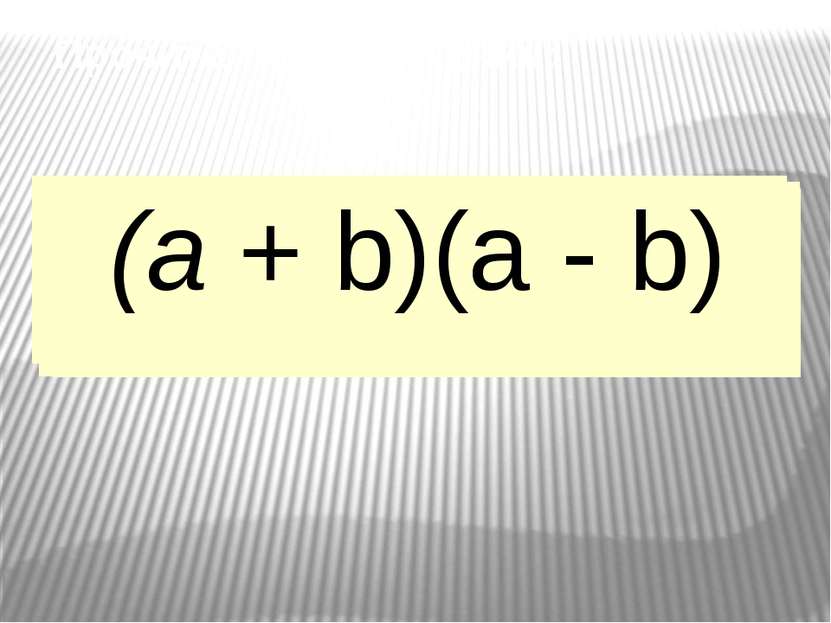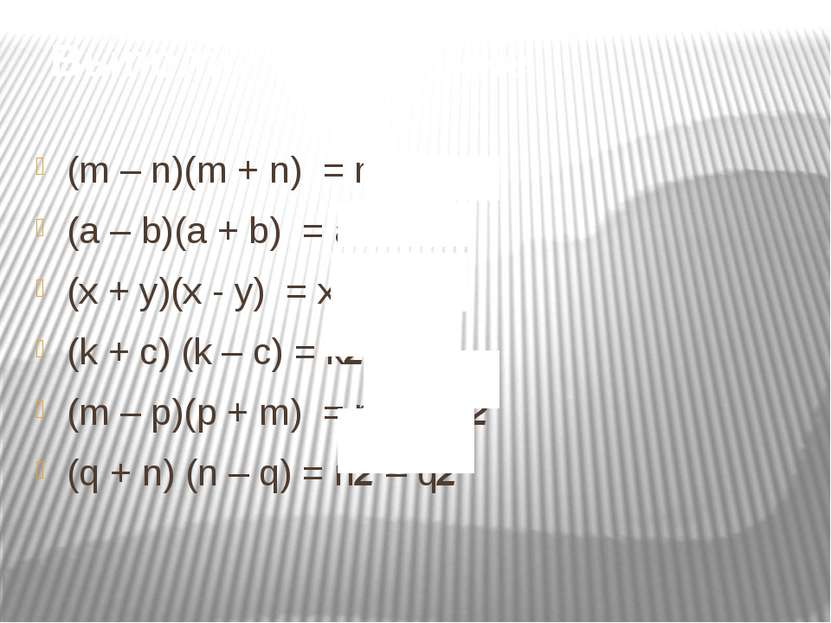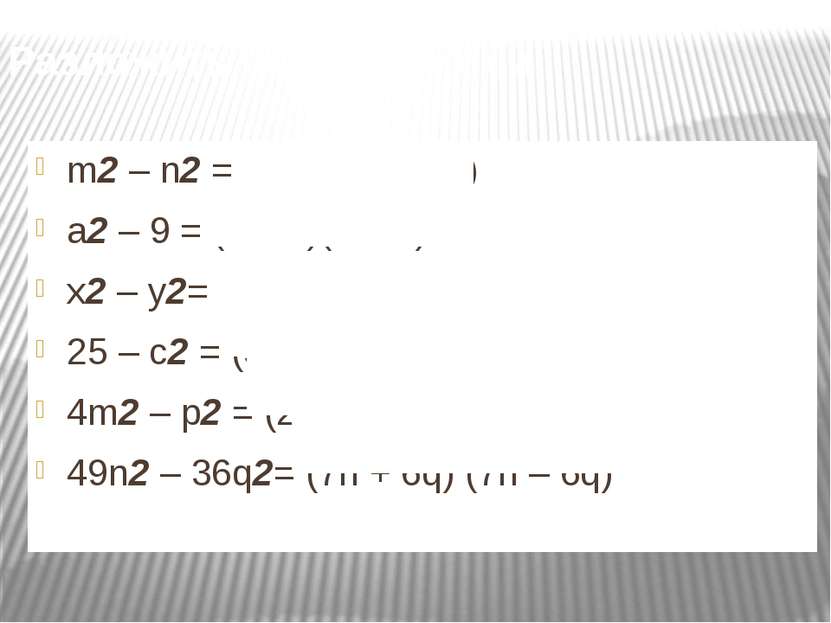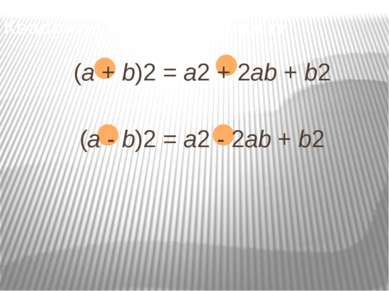X
Код презентации скопируйте его
Формулы сокращенного умножения. Разложение на множители
Скачать эту презентацию
Презентация на тему Формулы сокращенного умножения. Разложение на множители
Скачать эту презентациюCлайд 1
ФОРМУЛА РАЗНОСТИ КВАДРАТОВ
Cлайд 2
Разложить на множители: 7 + 7ху 5х2 + 9х 3а2х – 2 ах2 14с 5 – 7с 4 5а + 10 ав + 5 в 2
Cлайд 3
Разложить на множители: а(х+ у) + 5(х + у) 6х(а – 2к) + (а – 2к) с(у – 2) – (2 – у) а(х - у) + а(х + у) а(х - у) + 5(у - х) 6(а – к) - (к - а) (у – 1) 2 – (у - 1)х а(х - у) + а(х + у)
Cлайд 4
Прочитайте выражения: а + b (а + b)2 а2 + b2 х – у (х – у)2 х2 – у2
Cлайд 5
Найдите квадраты следующих выражений: с, 4р; - m; 5х2у3. - 3 , 0,6х; 2в3
Cлайд 6
Найдите удвоенное произведение выражений 3 и 4 с и 6 3х и у 2а и 5к 8 и 5в2 ав и – 3в .
Cлайд 7
Выполните умножение (х + 6)(х – 5)
Cлайд 8
Запишите выражения: Квадрат суммы а и в Квадрат суммы х и у Квадрат суммы m и n
Cлайд 9
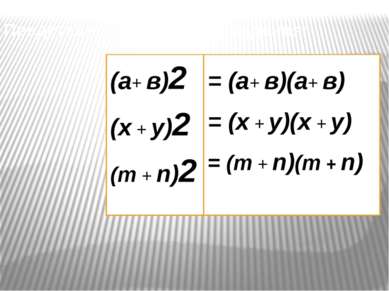Представьте в виде произведения: (а+ в)2 (х + у)2 (m + n)2 = (а+ в)(а+ в) = (х + у)(х + у) = (m + n)(m + n)
Cлайд 10
Выполните умножение и приведите подобные слагаемые: (а+ в)2 (х + у)2 (m + n)2 = а 2 + 2ав + в2 = х 2 + 2ху + у2 = m 2 + 2mn + n2
Cлайд 11
Запишите выражения: Квадрат разности а и в Квадрат разности х и у Квадрат разности m и n
Cлайд 12
Представьте в виде произведения: (а - в)2 (х - у)2 (m - n)2 = (а - в)(а - в) = (х - у)(х - у) = (m - n)(m - n)
Cлайд 13
Выполните умножение и приведите подобные слагаемые: = а 2 – 2ав + в2 = х 2 – 2ху + у2 = m 2 – 2mn + n2 (а - в)2 (х - у)2 (m - n)2
Cлайд 14
Квадраты суммы и разности (а + b)2 = a2 + 2ab + b2 (а - b)2 = a2 - 2ab + b2
Cлайд 15
Задание ответ (с + 11)2 с2 + 22с + 121 (7у + 6)2 49у2 + 84у + 36 (9 – 8у)2 81 – 144у + 64у2 (1/3 х – 3у)2 1/9 х2 – 2ху + 9у2 (0,3с – 12а)2 0,09с2 – 7,2ас + 144а2
Cлайд 16
Прочитайте выражения: а + b (а + b)2 а2 + b2 х – у (х – у)2 х2 – у2 а2 – с2 ху с(а + у) х(а – у) (а + с)(х - у) (а - с)(х + у) (к + с)(к - с) (х - у)(х + у) (а + b)(a - b)
Cлайд 17
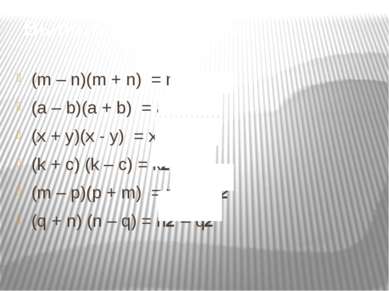Выполни умножение (m – n)(m + n) = m2 – n2 (a – b)(a + b) = a2 – b2 (x + y)(x - y) = x2 – y2 (k + c) (k – c) = k2 – c2 (m – p)(p + m) = m2 – p2 (q + n) (n – q) = n2 – q2
Cлайд 18
Вычислить: (10 + 1) 2 = 100 + 20 + 1 = 121 (100 - 1) 2 = 10000 - 200 + 1 = 9 801 61 2 = (60 + 1) 2 = 199 2 =
Cлайд 19
Выполните умножение (3x + 4)(3x - 4) = (2 - 5n)(5n + 2)= (с2 + 4x)(4x - c2)= (9p + 4a)(9p - 4a) = (5 - 6b2)(5 + 6b2) = (0,7a3-1)(0,7a3+1) =
Cлайд 20
Разложение на множители 1… представление многочлена в виде суммы двух или нескольких многочленов 2…представление многочлена в виде произведения двух или нескольких одночленов 3…представление многочлена в виде произведения двух или нескольких многочленов
Cлайд 21
Способы разложения на множители Вынесение общего множителя за скобки Способ группировки Формулы сокращенного умножения
Cлайд 22
Разложить на множители: 4х + 4ху х2 + 7х а2х – 2ах2 2с 5 – 6с 4
Cлайд 23
Разложить на множители: к(х - у) + 4(х - у) 6(к – 2) + (к – 2) с(у – 1) – а(1 – у) а(х - у) + 2(у - х)
Cлайд 24
Разложить на множители:
Cлайд 25
Разложить на множители: m2 – n2 = (m – n)(m + n) a2 – 9 = (a – 3)(a + 3) x2 – y2= (x + y)(x - y) 25 – c2 = (5 + c) (5 – c) 4m2 – p2 = (2m – p)(2p + m) 49n2 – 36q2= (7n + 6q) (7n – 6q)
Cлайд 26
Решаем примеры: Представить в виде многочлена: (x+4)(x-4)=x2-16 ( 3-m)(3+m)=9-m2 (8+y)(y-8)=y2-64 Разложить на множители: с2-25=(с-5)(с+5) 81-p2=(9+p)(9-p) 0,36-y2=(0,6-y)(0,6+y) Разность квадратов
Cлайд 27
Cлайд 28
= =
Cлайд 29
Решаем примеры: Решаем примеры: Представить в виде многочлена: (x+4)(x-4)=x2-16 ( 3-m)(3+m)=9-m2 (8+y)(y-8)=y2-64 Разложить на множители: с2-25=(с-5)(с+5) 81-p2=(9+p)(9-p) 0,36-y2=(0,6-y)(0,6+y)
Cлайд 30
Проверочная самостоятельная работа. №1.Преобразуйте в много- член: а)(3а+с)² = б)(у -5)(у +5)= в)(4в +5с)(5с -4в)= №2.Разложите на множители: а)16у² – 25= б)а² -6ав +9в² = №3.Решите уравнение: 12-(4- х)² =х(3 – х)
