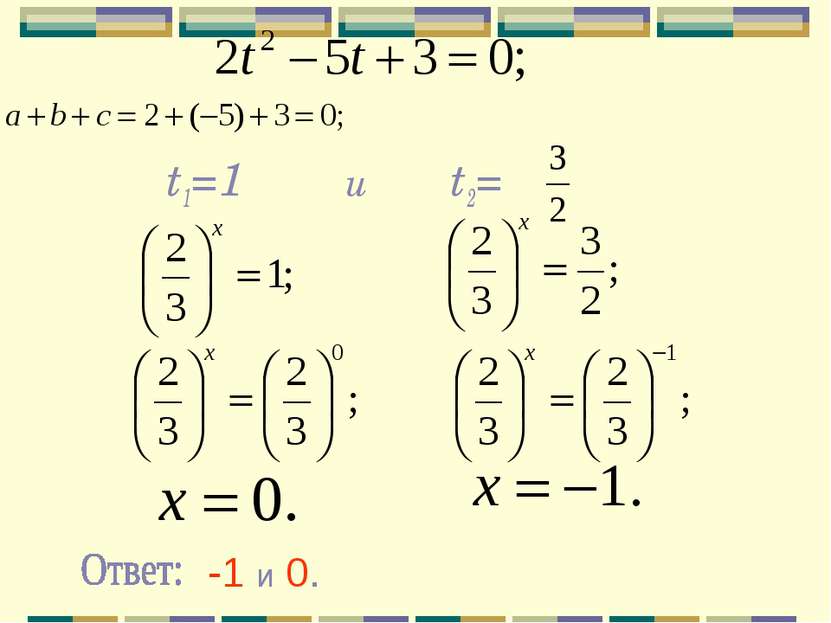X
Код презентации скопируйте его
Показательные уравнения (11 класс)
Скачать эту презентацию
Презентация на тему Показательные уравнения (11 класс)
Скачать эту презентациюCлайд 1
Урок по теме «Показательные уравнения 11 класс (новая тема - 2часа). Разработан учителем математики высшей квалификационной категории МОБУ СОШ №2 с углубленным изучением отдельных предметов г.Шимановска Амурской области Андреевой Ольгой Алексеевной.
Cлайд 2
1).Представить выражение в виде степени с рациональным показателем:
Cлайд 3
2).Вычислить: 3).Найти область определения выражения:
Cлайд 4
4).Разложить на множители: Выносим степень с меньшим показателем!
Cлайд 5
4).Какие из перечисленных функций показательные:
Cлайд 6
5).Какие из перечисленных функций возрастают, какие убывают:
Cлайд 7
6).Дана функция у=6 и значения у, равные 1,5; 12; 6; . Выбрать те значения у, при которых х
Cлайд 8
Все уравнения можно рассматривать, как равенства двух функций f(x) =φ(x). Задача решения уравнений заключается в отыскании всех тех значений х, для каждого из которых значения функций f(x) и φ(x) равны между собой. Областью определения уравнения называется общая часть областей определения каждой из функций. Обычно вид уравнения определяется функцией, содержащейся в этом уравнении: линейное, квадратичное, тригонометрическое и показательное.
Cлайд 9
Тема: «Решение показательных уравнений». Задачи урока: Познакомиться с видами показательных уравнений. Рассмотреть способы решений показательных уравнений различных видов. Отработать навыки и умения решения показательных уравнений.
Cлайд 10
I.Простейшие показательные уравнения вида а). D(у)=R; Е(у)= Монотонна на всей области определения, при a >1 возрастает,при 0< a 0; Не имеет корней при b 0. Представим b в виде имеем:
Cлайд 11
по свойству степеней с одинаковыми основаниями решением уравнения является равенство х = с. Пример: Ответ: 4.
Cлайд 12
2).В уравнении , левая и правая части приведены к одному основанию и решением уравнения является равенство х = Т.к. разделим обе части уравнения на правую часть: 3).Очевидно, что уравнение Пример:
Cлайд 13
II. Показательные уравнения вида а). На основании определения о нулевом показателе имеем его решение: Пример: Ответ: 2 и 3. б). Уравнения такого вида решаются с использованием теорем о возведении в степень произведения и дроби и им обратные, рассмотрим решение на примере:
Cлайд 14
Пример 1: Т.к. Пример 2: Т.к.
Cлайд 15
III. Показательные уравнения вида где Вынесем за скобки где -наименьшее число. Имеем: при N≠0 получим уравнение:
Cлайд 16
Возможны три случая: , уравнение сводится к виду , уравнение сводится к виду , данное уравнение не имеет корней.
Cлайд 17
Пример 1: Вынесем за скобки Пример 2: Вынесем за скобки уравнение корней не имеет. корней нет.
Cлайд 18
IV. Трёхчленное показательное уравнение: а). Выполним подстановку где у>0, показательное уравнение превращается в обычное квадратное уравнение Решением этого уравнения являются значения Чтобы найти корни показательного уравнения нужно решить уравнения и Если и одновременно, то данное показательное уравнение корней не имеет.
Cлайд 19
Пример: Выполним подстановку где t>0, Решим уравнение -посторонний корень;
Cлайд 20
б). Разделим данное уравнение на bx, ( bx≠0): Решение этого уравнения сводится к решению квадратного уравнения: Чтобы найти корни показательного уравнения нужно решить уравнения и y>0 где
Cлайд 21
Пример: Преобразуем уравнение по свойствам степени: Разделим уравнение на 32х, 32х≠0: выполним подстановку Решим уравнение
Cлайд 22
t1=1 t2= и -1 и 0.
Cлайд 23
Ответить на вопросы: Какие уравнения называются показательными? Сколько корней имеет уравнение вида: Когда показательное уравнение не имеет корней?
Cлайд 24
Устно: решить показательные уравнения (по выбору): 5х=625; 5-х= 25; 100х=10; 12х=1; 2-х=8; 5х∙2х=400; 4х=256; 4х=2 ; 10х+1=0,1; 3х-1= 27; 27х=3 ; 5х-2= 25; ах=а2; 2х∙3х=36; 5х=-25.
Cлайд 25
Работа в группах. Выполнить задания из учебника: Группы Ι и III решают: №460(б), №461(б), №462(а), №463(в), №464(в), №469(в). Группы II и IV решают: №460(г), №461(г), №462(а), №463(г), №464(г), №469(а).
Cлайд 26
к виду к виду не имеет корней. К виду К виду Формулы решения показательных уравнений где
Cлайд 27
Индивидуальная работа. Из данных вариантов решить один(по выбору): Дополнительно: Дополнительно: III уровень +1б. +1б. +1б. +1б. +1б. а).24х=16; б).3х=1. а).33х=27; б).4х=-64. +1б. II уровень I уровень Вариант №1. Вариант №2. Вариант №3. Вариант №4. Вариант №5. Вариант №6.
Cлайд 28
Итоги урока. Какие уравнения называются показательными? К какому типу уравнений относятся показательные уравнения? Почему? Какие виды показательных уравнений рассмотрели? Сколько решений может иметь показательное уравнение? Когда оно не имеет корней? Домашнее задание: Теория п.36.1, №463(а), №464(б), №468(в), №469(б).
