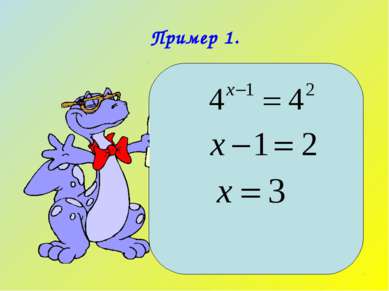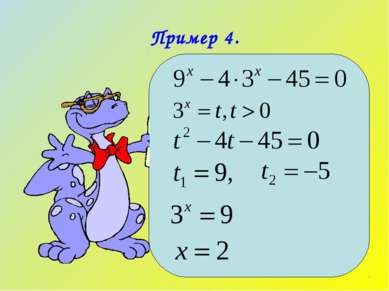Войти
X

Код презентации скопируйте его

Ширина px

Вы можете изменить размер презентации, указав свою ширину плеера!

Показательные уравнения (10 класс)

Скачать эту презентацию

Получить код Увеличить
Математический диктант Запишите функции Математический диктант 1. Постройте схематично графики. 2. Выпишите убывающие... Показательное уравнение – это уравнение, в котором неизвестное содержится в п... Пример 1. 2. Чтобы привести уравнение к виду (1) необходимо в левой части уравнения вын... Пример 2. 3. Можно разделить обе части уравнения на выражение, не равное нулю Пример 3. 4. Некоторые показательные уравнения заменой сводятся к квадратным. Надо помн... Пример 4. Алгоритм решения показательных уравнений 1. Уравниваем основания степеней во ... Графическое решение уравнения сводится к построению графиков функций левой и ... Пример 5. Решение уравнений На сайте matematika.school9sever.edusite.ru в разделе 10 кл... Домашнее задание § 8 (задачи 1-6), №№ 140 (2,4), 143 (2,4), 145 (2,4)
1 18

Презентация на тему Показательные уравнения (10 класс)

Скачать эту презентацию

Cлайд 1
Cлайд 2
Математический диктант Запишите функции Математический диктант Запишите функции
Cлайд 3
Математический диктант 1. Постройте схематично графики. 2. Выпишите убывающие... Математический диктант 1. Постройте схематично графики. 2. Выпишите убывающие функции 3. Для каждой из функций запишите множество значений. 4. Определите для каждой функции точку пересечения с осью ординат 1. Постройте схематично графики. 2. Выпишите возрастающие функции 3. Для каждой из функций запишите множество значений. 4. Определите для каждой функции точку пересечения с осью ординат
Cлайд 4
Показательное уравнение – это уравнение, в котором неизвестное содержится в п... Показательное уравнение – это уравнение, в котором неизвестное содержится в показателе степени. Показательное уравнение сводится к виду Такое уравнение имеет единственный корень
Cлайд 5
Пример 1. Пример 1.
Cлайд 6
2. Чтобы привести уравнение к виду (1) необходимо в левой части уравнения вын... 2. Чтобы привести уравнение к виду (1) необходимо в левой части уравнения вынести за скобки общий множитель
Cлайд 7
Пример 2. Пример 2.
Cлайд 8
3. Можно разделить обе части уравнения на выражение, не равное нулю 3. Можно разделить обе части уравнения на выражение, не равное нулю
Cлайд 9
Пример 3. Пример 3.
Cлайд 10
4. Некоторые показательные уравнения заменой сводятся к квадратным. Надо помн... 4. Некоторые показательные уравнения заменой сводятся к квадратным. Надо помнить, что t>0, так как показательная функция не может принимать значения отрицательные и равные нулю.
Cлайд 11
Пример 4. Пример 4.
Cлайд 12
Алгоритм решения показательных уравнений 1. Уравниваем основания степеней во ... Алгоритм решения показательных уравнений 1. Уравниваем основания степеней во всех слагаемых, содержащих неизвестное в показателе степени. 2. а) Если показатели степеней отличаются только постоянным слагаемым, то выносим за скобки общий множитель. б) Если показатель одной из степеней по модулю в 2 раза больше показателя другой, то вводим новую переменную.
Cлайд 13
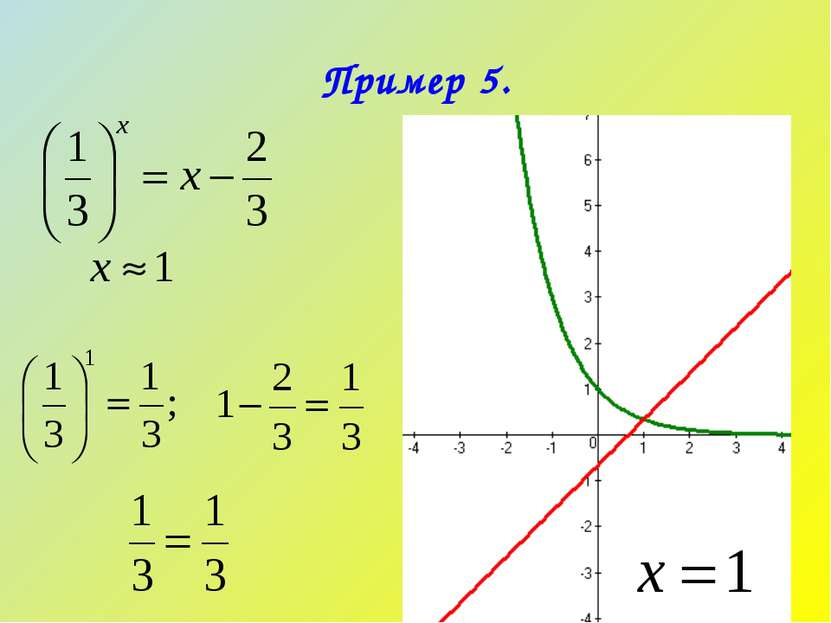
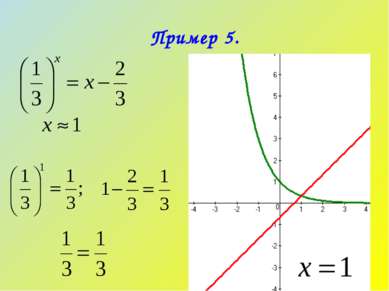
Графическое решение уравнения сводится к построению графиков функций левой и ... Графическое решение уравнения сводится к построению графиков функций левой и правой частей уравнения, нахождению по рисунку примерного значения абсциссы точки пересечения графиков. Если возможно, с помощью проверки уточняется корень уравнения.
Cлайд 14
Пример 5. Пример 5.
Cлайд 15
Решение уравнений На сайте matematika.school9sever.edusite.ru в разделе 10 кл... Решение уравнений На сайте matematika.school9sever.edusite.ru в разделе 10 класс выполнить тренировочный тест по теме «Показательные уравнения»
Cлайд 16
Cлайд 17
Cлайд 18
Домашнее задание § 8 (задачи 1-6), №№ 140 (2,4), 143 (2,4), 145 (2,4) Домашнее задание § 8 (задачи 1-6), №№ 140 (2,4), 143 (2,4), 145 (2,4)

Презентации этого автора

Скачать эту презентацию

Похожие презентаци


Поделится
Наверх