X
Код презентации скопируйте его
Методы решения квадратных уравнений
Скачать эту презентациюПрезентация на тему Методы решения квадратных уравнений
Скачать эту презентациюCлайд 2
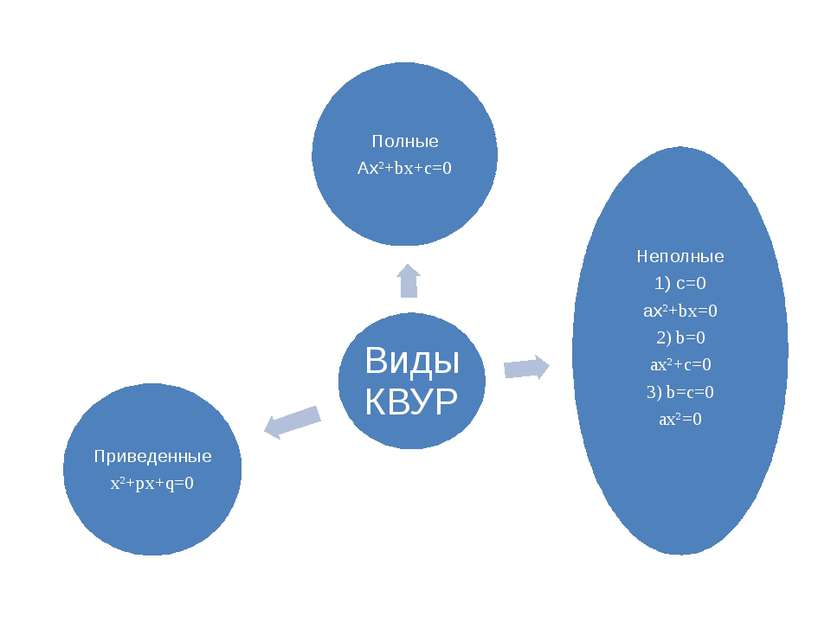
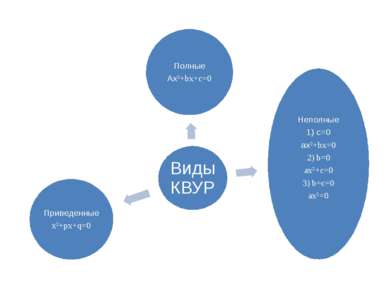
 Определение Квадратные уравнения (КВУР) – уравнения вида ax²+bx+c=0, где x – переменная, a, b и c – любые числа, причем a≠0. (В случае, когда а = 0, КВУР переходит в класс линейных уравнений, т.к. исключается переменная во второй степени)
Определение Квадратные уравнения (КВУР) – уравнения вида ax²+bx+c=0, где x – переменная, a, b и c – любые числа, причем a≠0. (В случае, когда а = 0, КВУР переходит в класс линейных уравнений, т.к. исключается переменная во второй степени)
Cлайд 4
 Методы решения. Неполные КВУР. I. ax²+bx=0 1) Вынести общий множитель за скобки и разложить на множители: x·(ax+b)=0 x=0 или ax+b=0
Методы решения. Неполные КВУР. I. ax²+bx=0 1) Вынести общий множитель за скобки и разложить на множители: x·(ax+b)=0 x=0 или ax+b=0
Cлайд 5
 Методы решения. Неполные КВУР. 1) 2x²+3x=0 x(2x+3)=0 x=0 или 2x+3=0 2x=-3 x=-1,5 Ответ: -1,5; 0 2) 5u²-4u=0 u(5u-4)=0 u=0, u=0, u=0, 5u-4=0; 5u=4; u=0,8. Ответ: 0; 0,8. Примеры:
Методы решения. Неполные КВУР. 1) 2x²+3x=0 x(2x+3)=0 x=0 или 2x+3=0 2x=-3 x=-1,5 Ответ: -1,5; 0 2) 5u²-4u=0 u(5u-4)=0 u=0, u=0, u=0, 5u-4=0; 5u=4; u=0,8. Ответ: 0; 0,8. Примеры:
Cлайд 6
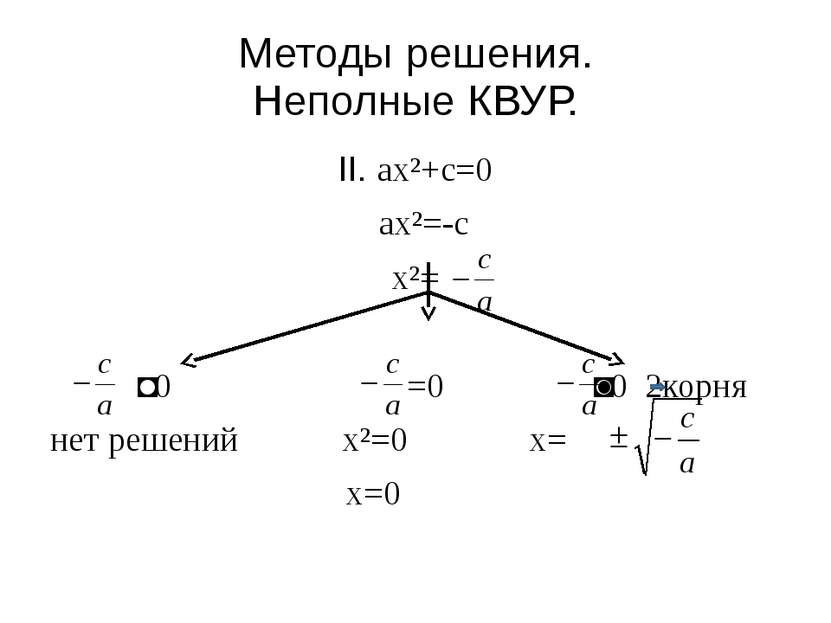
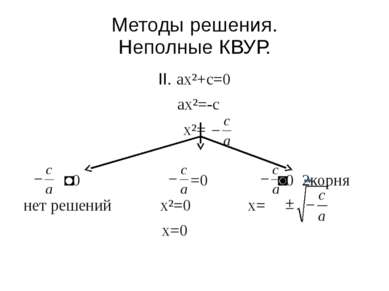 Методы решения. Неполные КВУР. II. ax²+c=0 ax²=-c x²= ˂0 =0 ˃0 2корня нет решений x²=0 x= x=0
Методы решения. Неполные КВУР. II. ax²+c=0 ax²=-c x²= ˂0 =0 ˃0 2корня нет решений x²=0 x= x=0
Cлайд 7
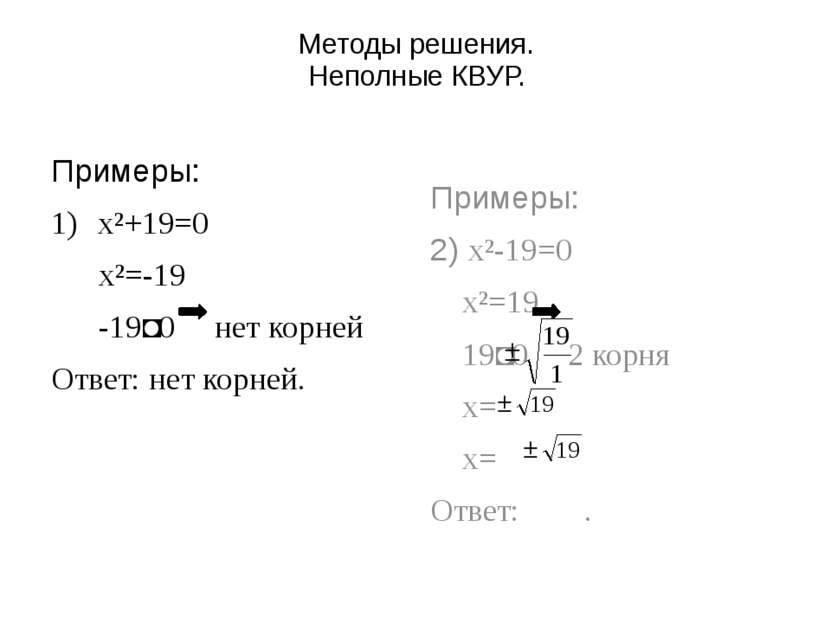
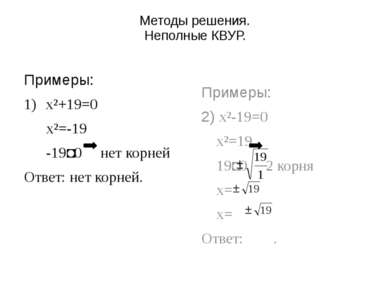 Методы решения. Неполные КВУР. Примеры: x²+19=0 x²=-19 -19˂0 нет корней Ответ: нет корней. Примеры: 2) x²-19=0 x²=19 19˂0 2 корня x= x= Ответ: .
Методы решения. Неполные КВУР. Примеры: x²+19=0 x²=-19 -19˂0 нет корней Ответ: нет корней. Примеры: 2) x²-19=0 x²=19 19˂0 2 корня x= x= Ответ: .
Cлайд 9
 Методы решения. Выделение полного квадрата. b=четное x²-4x+3=0 x²-2·x·2+4-4+3=0 (x-2)²-1=0 (x-2)²=1 x-2=± x-2= x=3 или x=1 Ответ:1, 3. b=нечетное 2x²+x+2=0 | :2 x²+ x+1=0 x²+2·x· + - +1=0 (x+0,25)²+ =0 (x+0,25)²= - ˂0 =˃ нет корней Ответ: нет корней.
Методы решения. Выделение полного квадрата. b=четное x²-4x+3=0 x²-2·x·2+4-4+3=0 (x-2)²-1=0 (x-2)²=1 x-2=± x-2= x=3 или x=1 Ответ:1, 3. b=нечетное 2x²+x+2=0 | :2 x²+ x+1=0 x²+2·x· + - +1=0 (x+0,25)²+ =0 (x+0,25)²= - ˂0 =˃ нет корней Ответ: нет корней.
Cлайд 10
 Методы решения. Полные КВУР ax²+bx+c=0 Формула полного квадрата: x²+8x+16=0 (x+4)²=0 x+4=0 x=-4 Ответ: x=-4. 2) a²-2,6a+1,69=0 (a-1,3)²=0 a-1,3=0 a=1,3 Ответ: a=1,3.
Методы решения. Полные КВУР ax²+bx+c=0 Формула полного квадрата: x²+8x+16=0 (x+4)²=0 x+4=0 x=-4 Ответ: x=-4. 2) a²-2,6a+1,69=0 (a-1,3)²=0 a-1,3=0 a=1,3 Ответ: a=1,3.
Cлайд 11
 Методы решения. Полные КВУР. Частные случаи. Теорема 1: Если a+b+c=0, то x =1, x = Примеры: 5x²-8x+3=0 5-8+3=0 Теорема1 x =1; x = . Ответ: x =1; x = . 2) 3x²-7x+4=0; 3-7+4=0 Теорема1 x =1; x = . Ответ: 1; .
Методы решения. Полные КВУР. Частные случаи. Теорема 1: Если a+b+c=0, то x =1, x = Примеры: 5x²-8x+3=0 5-8+3=0 Теорема1 x =1; x = . Ответ: x =1; x = . 2) 3x²-7x+4=0; 3-7+4=0 Теорема1 x =1; x = . Ответ: 1; .
Cлайд 12
 Методы решения. Полные КВУР. Частные случаи. Теорема 2: Если a-b+c=0, то x =-1, x =- . Примеры: 1) 5x²+9x+4=0 5-9+4=0 Теорема2 x =-1; x =- . Ответ: x =-1; x =- . 2) y²-22y-23=0 1+22-23= 0 Теорема2 x =-1; x =- x =23. Ответ:-1; 23.
Методы решения. Полные КВУР. Частные случаи. Теорема 2: Если a-b+c=0, то x =-1, x =- . Примеры: 1) 5x²+9x+4=0 5-9+4=0 Теорема2 x =-1; x =- . Ответ: x =-1; x =- . 2) y²-22y-23=0 1+22-23= 0 Теорема2 x =-1; x =- x =23. Ответ:-1; 23.
Cлайд 13
 Методы решения. Приведенные КВУР. Теорема ВИЕТА: x²+px+q=0 (a=1) x1 +x2 =-p x *x =q Примеры: x²-6x+8=0 x =2; x =4 x +x =6 x +x =8 Ответ: 2, 4. y²-10y-24=0 y =-4; y =6 y +y =10 y *y =24 Ответ: y =-4; y =6.
Методы решения. Приведенные КВУР. Теорема ВИЕТА: x²+px+q=0 (a=1) x1 +x2 =-p x *x =q Примеры: x²-6x+8=0 x =2; x =4 x +x =6 x +x =8 Ответ: 2, 4. y²-10y-24=0 y =-4; y =6 y +y =10 y *y =24 Ответ: y =-4; y =6.
Cлайд 14
 Методы решения. «Переброска» 1) 2x²-5x-3=0 x²-5x-3*2=0 x²-5x-6=0 (решим по Теореме 2) Корни запишем в виде: x = x = =3 Ответ: x =-0,5; x =3. 2) 3x²+2x-5=0 x²+2x-15=0 Решим по Теореме ВИЕТА. x = x = Ответ: ;
Методы решения. «Переброска» 1) 2x²-5x-3=0 x²-5x-3*2=0 x²-5x-6=0 (решим по Теореме 2) Корни запишем в виде: x = x = =3 Ответ: x =-0,5; x =3. 2) 3x²+2x-5=0 x²+2x-15=0 Решим по Теореме ВИЕТА. x = x = Ответ: ;
Cлайд 15
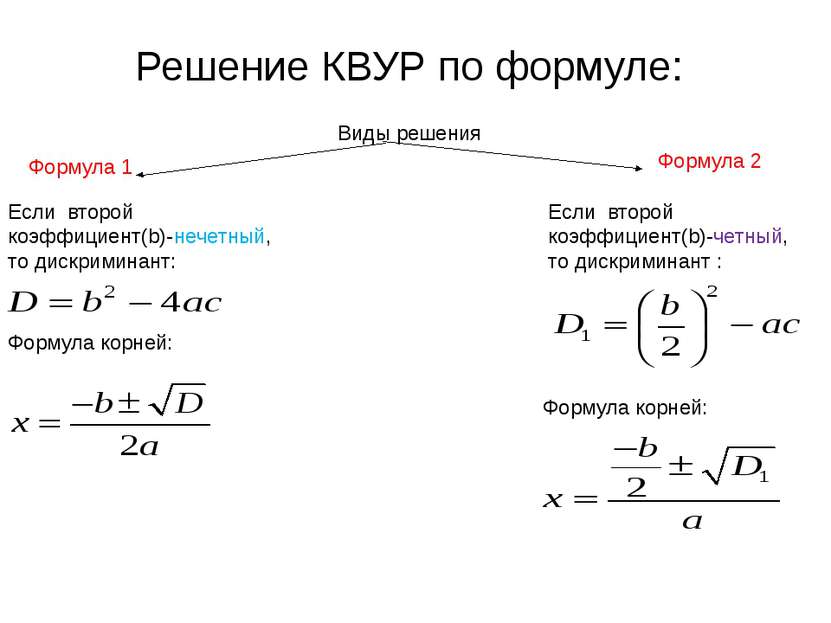
 Решение КВУР по формуле: Виды решения Формула корней: Если второй коэффициент(b)-четный, то дискриминант : Формула корней: Если второй коэффициент(b)-нечетный, то дискриминант: Формула 1 Формула 2
Решение КВУР по формуле: Виды решения Формула корней: Если второй коэффициент(b)-четный, то дискриминант : Формула корней: Если второй коэффициент(b)-нечетный, то дискриминант: Формула 1 Формула 2