X
Код презентации скопируйте его
Решение задач на нахождение площади поверхности и объемов тел вращения
Скачать эту презентацию
Презентация на тему Решение задач на нахождение площади поверхности и объемов тел вращения
Скачать эту презентациюCлайд 1
Презентацию подготовила: Учитель математики МБОУ СОШ №1 г.Воткинска, Удмуртской Республики Колесникова Татьяна Павловна
Cлайд 2
Найдите площадь поверхности (внешней и внутренней) шляпы, размеры которой (в см) указаны на рисунке. 1) Если дно шляпы опустить на плоскость её полей, то получим круг радиуса R = r1+ 10 = 20 cм. 2) Площадь этого круга 3) Найдем площадь боковой поверхности цилиндрической части 4) Найдем площадь шляпы Ответ: 1600 (см2). r1=10 10 10 Решение.
Cлайд 3
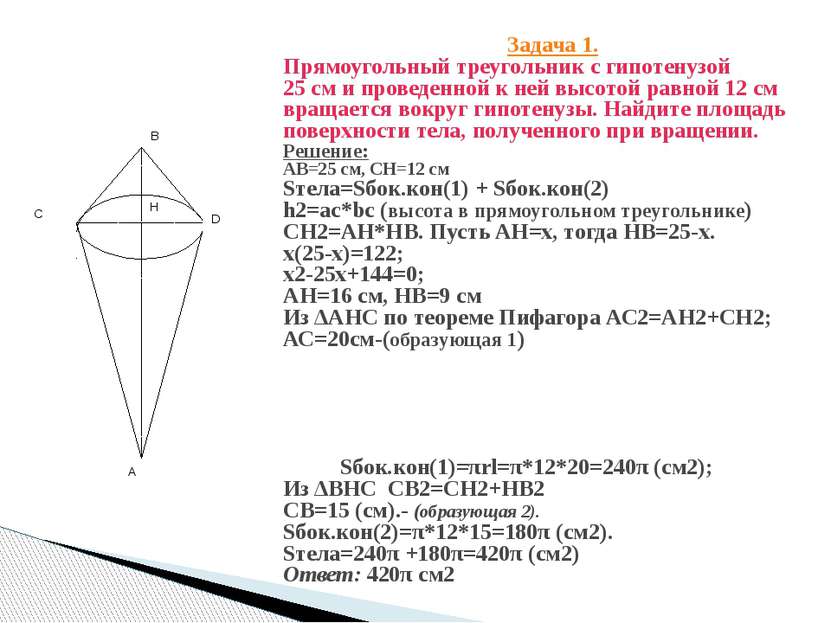
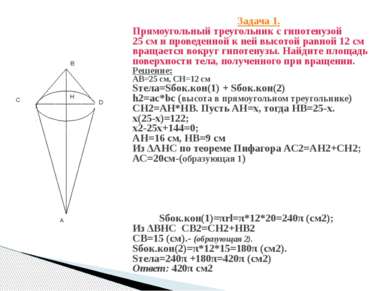Задача 1. Прямоугольный треугольник с гипотенузой 25 см и проведенной к ней высотой равной 12 см вращается вокруг гипотенузы. Найдите площадь поверхности тела, полученного при вращении. Решение: АВ=25 см, СН=12 см Sтела=Sбок.кон(1) + Sбок.кон(2) h2=ac*bc (высота в прямоугольном треугольнике) CH2=AH*HB. Пусть AH=x, тогда НВ=25-x. x(25-x)=122; x2-25x+144=0; АН=16 см, НВ=9 см Из ΔАНС по теореме Пифагора АС2=АН2+СН2; АС=20см-(образующая 1) Sбок.кон(1)=πrl=π*12*20=240π (cм2); Из ΔВНС СВ2=СН2+НВ2 CB=15 (см).- (образующая 2). Sбок.кон(2)=π*12*15=180π (см2). Sтела=240π +180π=420π (см2) Ответ: 420π см2 H B С А D
Cлайд 4
Задача 2. Прямоугольная трапеция с основаниями 5 см и 10 см и большей боковой стороной равной 13 см вращается вокруг большего основания. Найдите площадь поверхности тела вращения. Решение: АС=5 см, НК=10см, СК=13 см. ОК=НК-АС=5 см; l=13 см Из ΔСОК по теореме Пифагора СО2=СК2-ОК2; СО=r =12 см; Sбок.кон=πrl=π*12*13=156π (см2); Sцил.=2πrh+πr2=2π*12*5+144π=264π (см2); Sтела= Sбок.кон.+Sцил.= 156π +264π= =420π (см2); Ответ: 420π см2 А B C h O K H
Cлайд 5
Задача 3. Прямоугольная трапеция с основаниями 5 см и 10 см и большей боковой стороной равной 13 см вращается вокруг меньшего основания. Найдите площадь поверхности тела вращения. Решение: ВС=5 см, АD=10 см,АВ=13 см Sтела= Sбок.кон.+Sцил(1основание) Sтела= πrl+2πrh+πr2; АК=АD-ВС=5 (см); Из ΔАКВ - прямоугольного по теореме Пифагора КВ2=АВ2-АК2; КВ=12см – r AB=l – образующая h=AD=10 см Sтела=π*12*13 + 2π*12*10+144π=540π (см2). Ответ: 540π см2 K D А B C
Cлайд 6
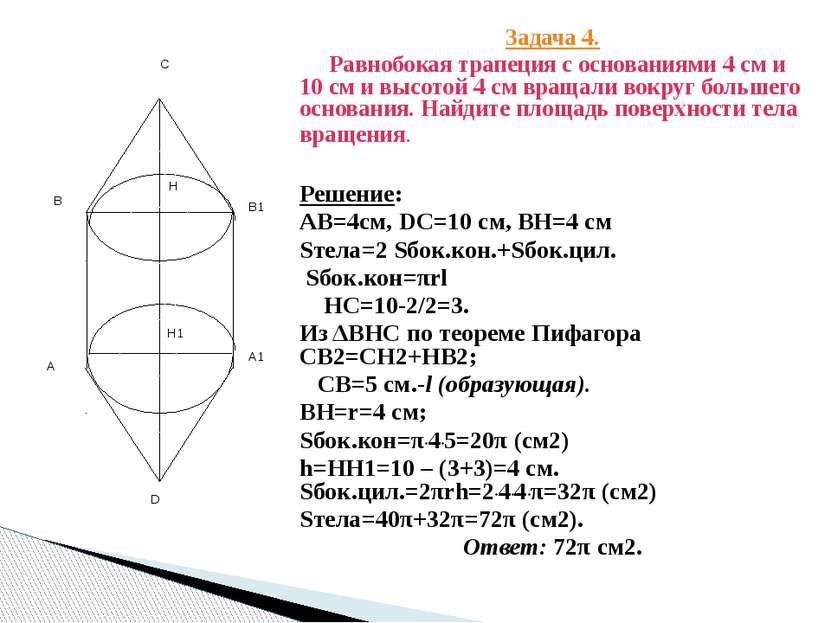
Задача 4. Равнобокая трапеция с основаниями 4 см и 10 см и высотой 4 см вращали вокруг большего основания. Найдите площадь поверхности тела вращения. Решение: АВ=4см, DC=10 см, ВН=4 см Sтела=2 Sбок.кон.+Sбок.цил. Sбок.кон=πrl HC=10-2/2=3. Из ΔВНС по теореме Пифагора СВ2=СН2+НВ2; CВ=5 см.-l (образующая). BH=r=4 cм; Sбок.кон=π*4*5=20π (см2) h=HH1=10 – (3+3)=4 см. Sбок.цил.=2πrh=2*4*4*π=32π (см2) Sтела=40π+32π=72π (см2). Ответ: 72π см2. B B1 D A1 H H1 С А
Cлайд 7
5
Cлайд 8
6
Cлайд 9
7
Cлайд 10
Дано два цилиндра. Объем первого равен 12 м3. Радиус основания второго в два раза меньше, чем первого, а высота в три раза больше. Требуется найти объем второго цилиндра. Решение: Объем цилиндра вычисляется по формуле:V=hπr² Отметим радиус основания первого цилиндра r а высоту h. Тогда радиус основания второго цилиндра равен r/2, а высота 3h. Подставим в указанную выше формулу и получим:V₂=3hπ(r/2)² Упростим полученное выражение: V₂=3hπ(r/2)² =3/4hπr²=3/4·12=9 Таким образом, объем второго цилиндра равен 9 м3. Ответ: 9.
Cлайд 11
Решите самостоятельно следующие задачи:
Cлайд 12
Решите самостоятельно следующие задачи:
