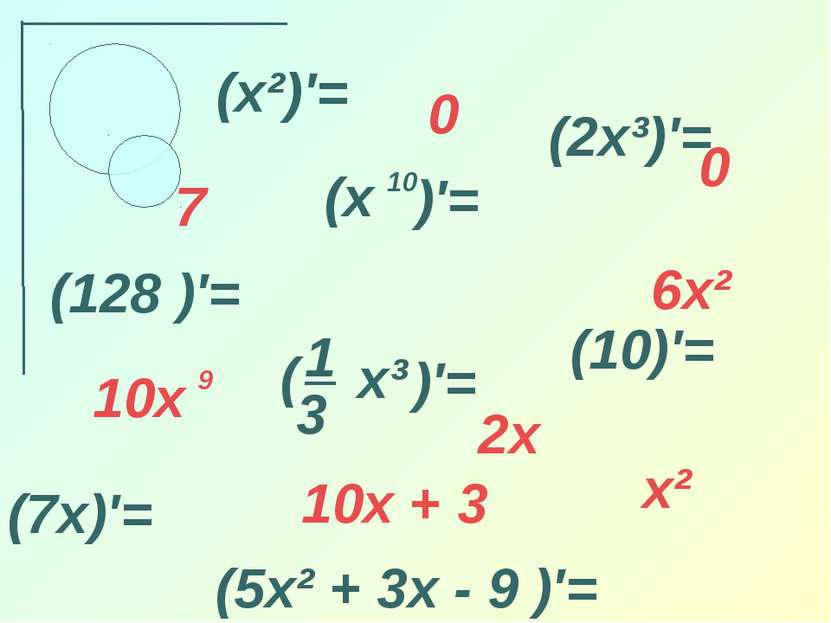X
Код презентации скопируйте его
Нахождение наибольшего и наименьшего значения функции
Скачать эту презентациюПрезентация на тему Нахождение наибольшего и наименьшего значения функции
Скачать эту презентациюCлайд 1
 Нахождение наибольшего и наименьшего значения функции (при решении задач прикладного характера). Через математические знания лежит широкая дорога к огромным, почти необозримым областям труда и открытий. Маркушевич А.И. Презентацию подготовила преподаватель 1 категории Керченского профессионального строительного лицея Селиванова Ирина Викторовна
Нахождение наибольшего и наименьшего значения функции (при решении задач прикладного характера). Через математические знания лежит широкая дорога к огромным, почти необозримым областям труда и открытий. Маркушевич А.И. Презентацию подготовила преподаватель 1 категории Керченского профессионального строительного лицея Селиванова Ирина Викторовна
Cлайд 3
 АЛГОРИТМ Найти точки экстремума функции, т. е. точки в которых производная равна нулю и меняет свой знак. Вычислить значение функции в этих точках и на концах отрезка, где определена функция. Выбрать из полученных значений оптимальное. Перевести задачу на язык математики, т. е. выразить искомую величину через функцию от некоторой переменной и найти область её определения.
АЛГОРИТМ Найти точки экстремума функции, т. е. точки в которых производная равна нулю и меняет свой знак. Вычислить значение функции в этих точках и на концах отрезка, где определена функция. Выбрать из полученных значений оптимальное. Перевести задачу на язык математики, т. е. выразить искомую величину через функцию от некоторой переменной и найти область её определения.
Cлайд 4
 Выполните задание: Найти промежутки возрастания и убывания функции. Найти экстремумы функции. Найти наибольшее и наименьшее значение функции на отрезке [-1;2] Y = N · x² - 2·N · x + 8
Выполните задание: Найти промежутки возрастания и убывания функции. Найти экстремумы функции. Найти наибольшее и наименьшее значение функции на отрезке [-1;2] Y = N · x² - 2·N · x + 8
Cлайд 5
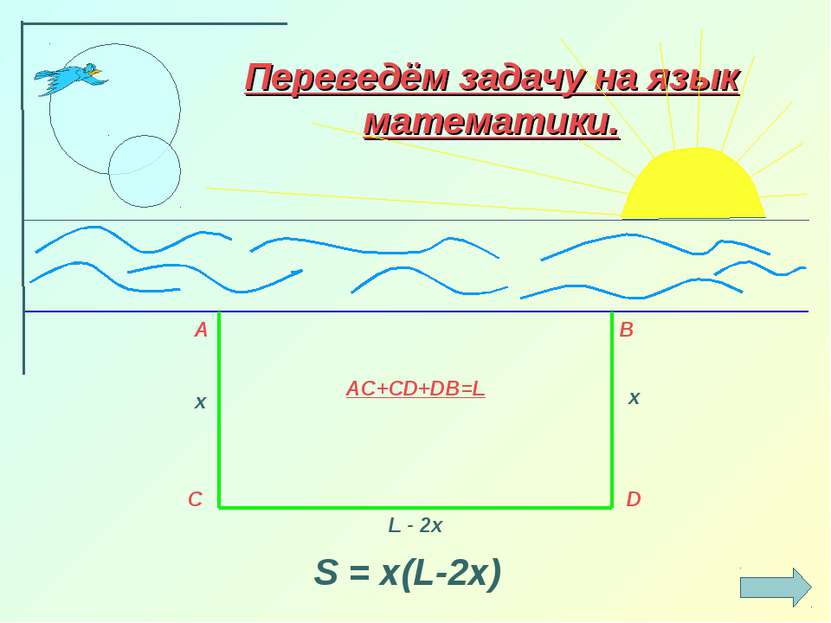
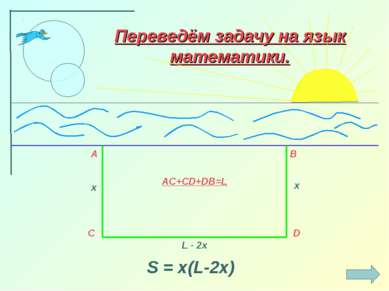
 Легенда об основании Карфагена гласит, что когда финикийский корабль пристал к берегу, местные жители согласились продать прибывшим столько земли, сколько можно огородить её одной бычьей шкурой. Но хитрая царица Дидона разрезала эту шкуру на ремешки, связала их и огородила полученным ремнём большой участок земли, примыкавший к побережью. Вопрос: какую наибольшую площадь земли могли купить финикийцы?
Легенда об основании Карфагена гласит, что когда финикийский корабль пристал к берегу, местные жители согласились продать прибывшим столько земли, сколько можно огородить её одной бычьей шкурой. Но хитрая царица Дидона разрезала эту шкуру на ремешки, связала их и огородила полученным ремнём большой участок земли, примыкавший к побережью. Вопрос: какую наибольшую площадь земли могли купить финикийцы?
Cлайд 7
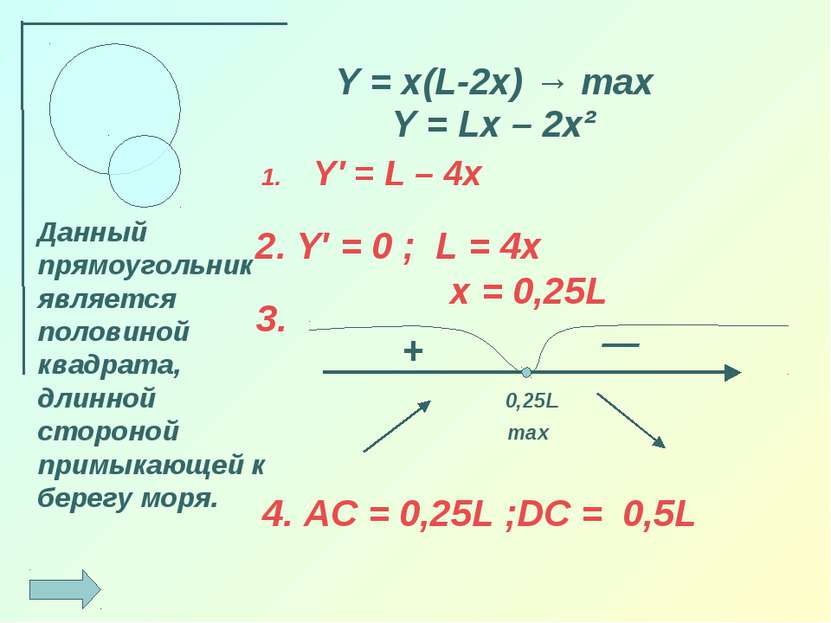
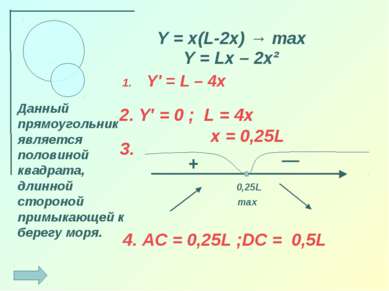 Y′ = L – 4x Y = x(L-2x) → max 0,25L + — max Данный прямоугольник является половиной квадрата, длинной стороной примыкающей к берегу моря. 2. Y′ = 0 ; L = 4x x = 0,25L 3. 4. AC = 0,25L ;DC = 0,5L Y = Lx – 2x²
Y′ = L – 4x Y = x(L-2x) → max 0,25L + — max Данный прямоугольник является половиной квадрата, длинной стороной примыкающей к берегу моря. 2. Y′ = 0 ; L = 4x x = 0,25L 3. 4. AC = 0,25L ;DC = 0,5L Y = Lx – 2x²
Cлайд 8
 Стоимость (за один час перевозки) содержания баржи состоит из двух частей: стоимости топлива, пропорциональной кубу скорости баржи, и стоимости амортизации баржи ( зарплата команды, стоимость оборудования и т. д.). Общая стоимость содержания баржи за час выражается формулой: S = av³ + b, где v- скорость судна в км/ч, a и b – коэффициенты, заданные для каждого судна (для нашего а=0,005, b=40). Ясно, что расходы на топливо будут тем больше, чем быстрее движется корабль, остальные расходы от скорости не зависят. Казалось бы, чем медленнее движется корабль, тем дешевле его эксплуатация. Так ли это?
Стоимость (за один час перевозки) содержания баржи состоит из двух частей: стоимости топлива, пропорциональной кубу скорости баржи, и стоимости амортизации баржи ( зарплата команды, стоимость оборудования и т. д.). Общая стоимость содержания баржи за час выражается формулой: S = av³ + b, где v- скорость судна в км/ч, a и b – коэффициенты, заданные для каждого судна (для нашего а=0,005, b=40). Ясно, что расходы на топливо будут тем больше, чем быстрее движется корабль, остальные расходы от скорости не зависят. Казалось бы, чем медленнее движется корабль, тем дешевле его эксплуатация. Так ли это?
Cлайд 9
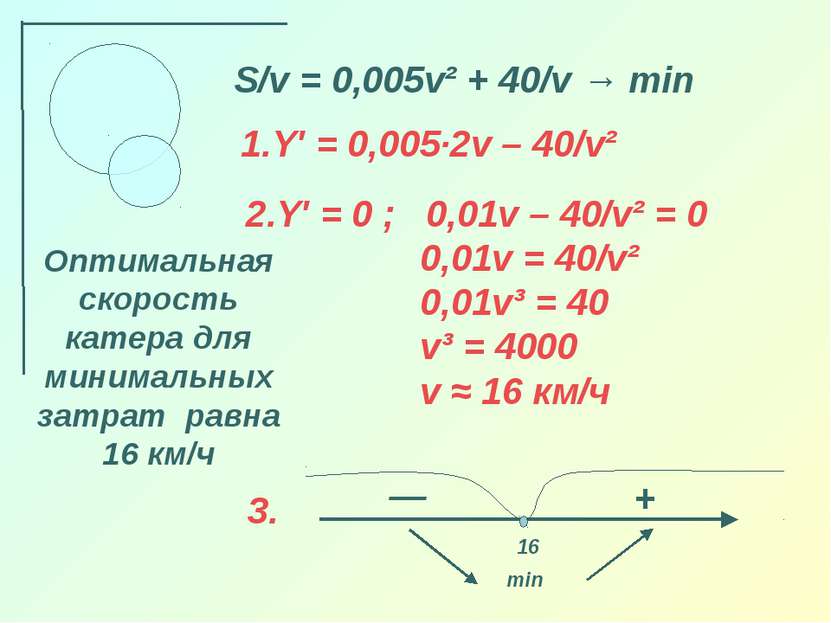
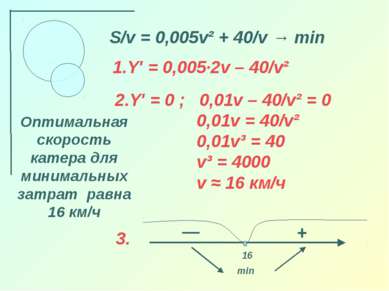 S/v = 0,005v² + 40/v → min Y′ = 0,005·2v – 40/v² — 16 + min Оптимальная скорость катера для минимальных затрат равна 16 км/ч 2.Y′ = 0 ; 0,01v – 40/v² = 0 0,01v = 40/v² 0,01v³ = 40 v³ = 4000 v ≈ 16 км/ч 3.
S/v = 0,005v² + 40/v → min Y′ = 0,005·2v – 40/v² — 16 + min Оптимальная скорость катера для минимальных затрат равна 16 км/ч 2.Y′ = 0 ; 0,01v – 40/v² = 0 0,01v = 40/v² 0,01v³ = 40 v³ = 4000 v ≈ 16 км/ч 3.
Cлайд 10
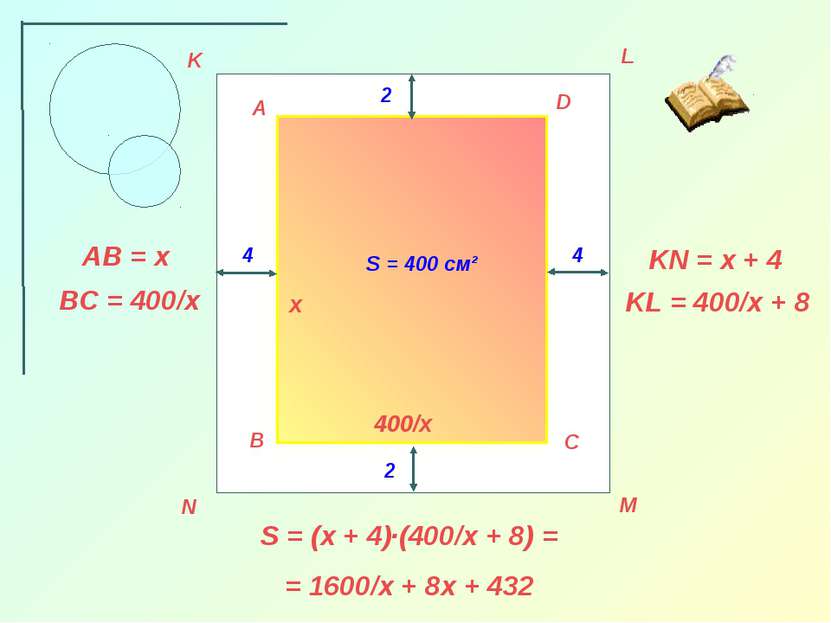
 Печатный текст (вместе с промежутками между строками) одной страницы книги должен занимать 400 см². Верхние и нижние поля страницы должны иметь ширину 2 см. Боковые – 4 см. Вопрос: каковы самые выгодные размеры страницы, исходя только из экономии бумаги?
Печатный текст (вместе с промежутками между строками) одной страницы книги должен занимать 400 см². Верхние и нижние поля страницы должны иметь ширину 2 см. Боковые – 4 см. Вопрос: каковы самые выгодные размеры страницы, исходя только из экономии бумаги?
Cлайд 11
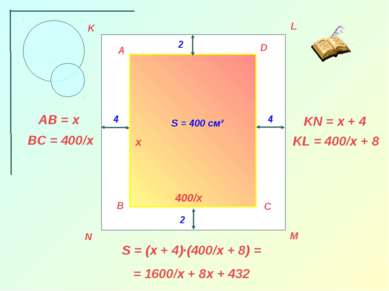 A B C D K L M N 4 4 2 2 S = 400 см² х 400/х AB = x BC = 400/x KL = 400/x + 8 KN = x + 4 S = (x + 4)·(400/x + 8) = = 1600/x + 8x + 432
A B C D K L M N 4 4 2 2 S = 400 см² х 400/х AB = x BC = 400/x KL = 400/x + 8 KN = x + 4 S = (x + 4)·(400/x + 8) = = 1600/x + 8x + 432
Cлайд 12
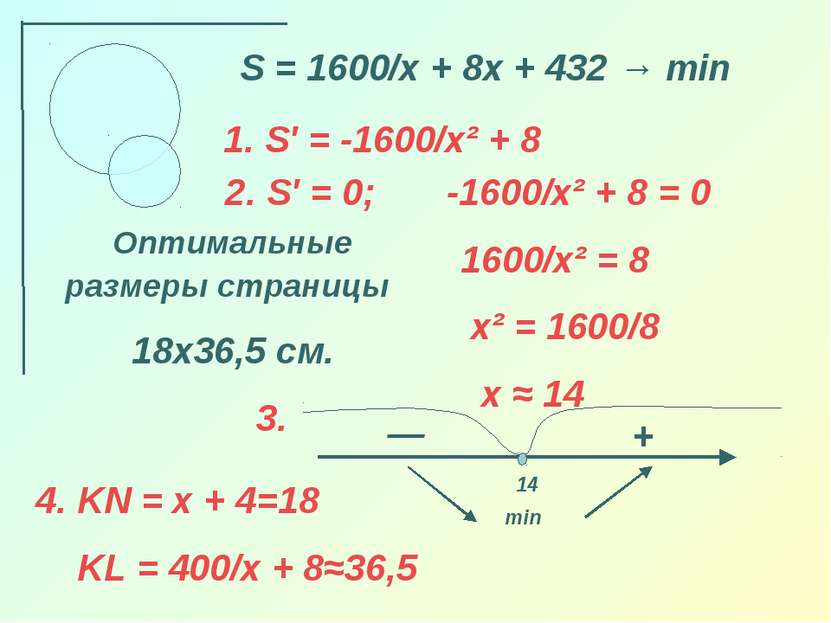
 S = 1600/x + 8x + 432 → min 1. S′ = -1600/x² + 8 2. S′ = 0; -1600/x² + 8 = 0 1600/x² = 8 x² = 1600/8 x ≈ 14 3. — + min 14 Оптимальные размеры страницы 18х36,5 см. 4. KN = х + 4=18 KL = 400/x + 8≈36,5
S = 1600/x + 8x + 432 → min 1. S′ = -1600/x² + 8 2. S′ = 0; -1600/x² + 8 = 0 1600/x² = 8 x² = 1600/8 x ≈ 14 3. — + min 14 Оптимальные размеры страницы 18х36,5 см. 4. KN = х + 4=18 KL = 400/x + 8≈36,5
Cлайд 13
 Вывод: Производная функции успешно применяется при решении оптимальных задач в различных сферах деятельности человека. Д/з решить задачу: Рекламный щит имеет форму прямоугольника S = 9 м². Изготовьте щит в виде прямоугольника с наименьшим периметром. Определите его стоимость, если суммарная цена материалов и работ по изготовлению за 1 м² составляет 200 грн + 25 грн за погонный метр длины щита.
Вывод: Производная функции успешно применяется при решении оптимальных задач в различных сферах деятельности человека. Д/з решить задачу: Рекламный щит имеет форму прямоугольника S = 9 м². Изготовьте щит в виде прямоугольника с наименьшим периметром. Определите его стоимость, если суммарная цена материалов и работ по изготовлению за 1 м² составляет 200 грн + 25 грн за погонный метр длины щита.