X
Код презентации скопируйте его
Удивительные числа
Скачать эту презентацию
Презентация на тему Удивительные числа
Скачать эту презентациюCлайд 1
Удивительные числа Авторы работы: Беляева Наталья, Ясюкевич Алина, 6 класс
Cлайд 2
Cлайд 3
Объект нашего исследования – натуральные числа. Предмет исследования – свойства этих чисел. Гипотеза: Если простые числа – это «кирпичики», из которых строятся все натуральные числа, то, «перекладывая» их, можно получить удивительные «числовые сооружения».
Cлайд 4
Цель исследования: Познакомиться с удивительными числами и установить роль простых чисел в изменении их свойств. Задачи: Описать способы поиска простых чисел. Рассмотреть свойства совершенных и дружественных чисел. Познакомиться с палиндромами и репьюнитами. Метод исследования – теоретический
Cлайд 5
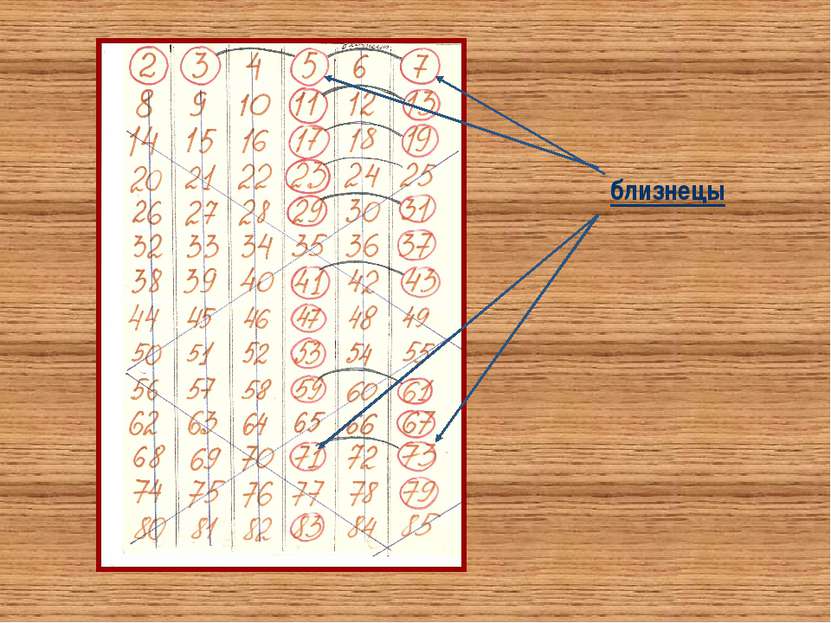
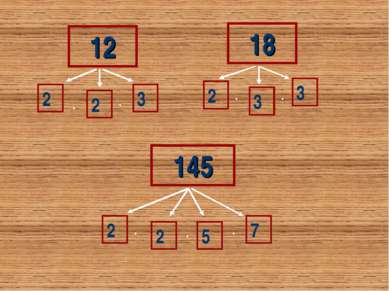
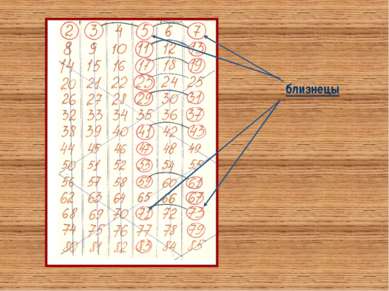
Простые числа Числа, которые имеют только два различных делителя, называются простыми 7=1·7 23=1·23 Самое маленькое простое число. Единственное четное среди простых 2
Cлайд 6
12 2 2 3 · · 18 2 3 3 · · 145 2 2 5 7 · · ·
Cлайд 7
Эратосфен
Cлайд 8
близнецы
Cлайд 9
Пьер Ферма 1601-1665 P=22 + 1 n
Cлайд 10
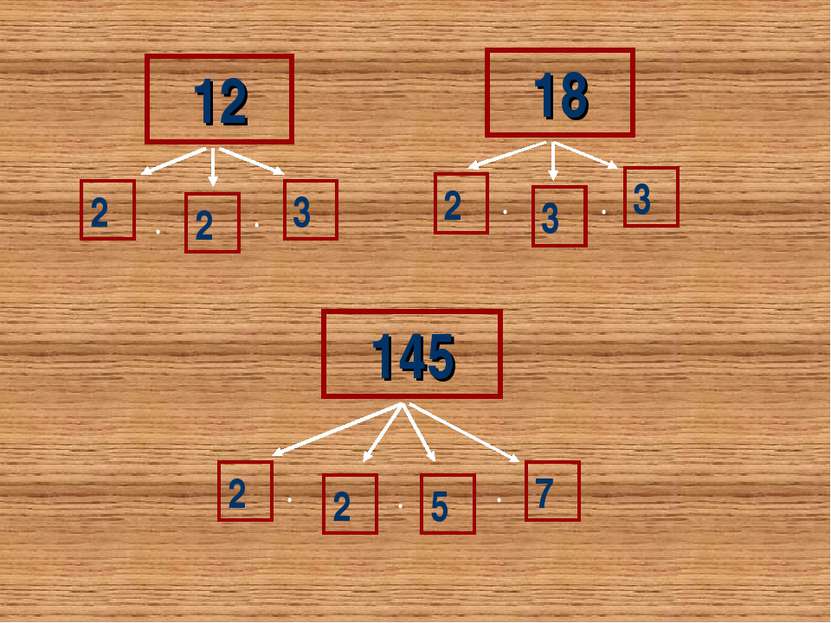
Совершенные числа Натуральное число n называется совершенным, если сумма всех его собственных делителей, отличных от самого n, в точности равна n. 6 + + 6 28 2 4 7 1 14 + + + + 28
Cлайд 11
Совершенные числа 6, 28, 496, 8128, 33550336… Вот 25-е число: 244496 . (244496-1) 26 790 цифр!!!
Cлайд 12
Пифагор 220 и 284 220 1 2 2 5 11 1+2+4+5+10+11+20+22+44+55+110=284 284 1 2 2 71 1+2+4+71+142=220
Cлайд 13
Дружественные числа Если сумма собственных делителей одного числа равна второму числу и, наоборот, сумма собственных делителей второго числа равна первому, то такие числа называют дружественными
Cлайд 14
Палиндромы и репьюниты Обращенное число – это число, записанное теми же цифрами, но расположенными в обратном порядке. Например, 1234 обращенное 4321. Палиндромическое число - равное обращенному. Например, 121, 5995, 12321 Репьюниты - натуральные числа, запись которых состоит только из единиц. В десятичной системе счисления репьюниты обозначаются короче: R1=1, R2=11, R3=111, R4=1111…
Cлайд 15
R2, R19, R23, R317 и R1031 – простые числа 111=3∙ 37; 1111=11∙101 11111=41∙271 111111=3∙7∙ 11∙13∙37 1111111=239∙ 4649 и т. д. 11∙11=121 11∙111=1221 1111∙11=12221 1112=12321
Cлайд 16
ВЫВОД простые числа – это «кирпичики», из которых строятся все натуральные числа. «перекладывая» их, можно получить удивительные «числовые сооружения»: СОВЕРШЕННЫЕ ЧИСЛА, ДРУЖЕСТВЕННЫЕ, РЕПЬЮНИТЫ
Cлайд 17
СПАСИБО ЗА ВНИМАНИЕ
