X
Код презентации скопируйте его
Выигрышная стратегия (3 класс)
Скачать эту презентацию
Презентация на тему Выигрышная стратегия (3 класс)
Скачать эту презентациюCлайд 1
Урок информатики в 3 классе Презентация подготовлена учителем информатики прогимназии № 1723 Волынниковой А.А. *
Cлайд 2
Люди придумали очень много разных игр: спортивных, настольных и т.д. Давайте поближе познакомимся с настольными играми. Эти игры можно разделить на два основных типа: игры, где всего два участника (соперника), например, нарды, и игры, в которых могут участвовать более двух игроков, например, лото. Игры, в которых участвуют только два игрока тоже можно разделить на две группы. К первой группе относятся игры, где игроки делают ходы по очереди и обдумывают каждый ход, потому что он зависит от действий соперника (например, шашки, шахматы). Ко второй группе можно отнести игры, где ходы игроков никак не зависят от ходов противника (морской бой, игры с кубиком и фишками). *
Cлайд 3
В ряде задач задается один и тот же вопрос: кто из двух игроков выиграет при правильной игре? Слова "правильная игра" означают, что если у кого-то из игроков есть стратегия, позволяющая выигрывать при любых ходах другого игрока, и он не делает "глупых" ходов, а стремится выиграть и следует своей выигрышной стратегии. В каждой задаче необходимо придумать такую стратегию для одного из игроков. *
Cлайд 4
В игре «Кто первым назовет число 100» участвуют двое. Один называет любое число от 1 до 9 включительно. Другой прибавляет к названному числу любое число от 1 до 9 и называет сумму. К этой сумме первый снова добавляет любое число от 1 до 9 и называет новую сумму. Выигрывает тот, кто назовет число 100. Кто выиграет при правильной игре? *
Cлайд 5
Многие простейшие игры имеют определенную закономерность и секрет выигрыша (выигрышную стратегию). В таких играх выигрышная стратегия зависит: от правил (условий) игры; от общего количества предметов, предложенных в игре; от выбора игроком первого или второго хода. Два карандаша по очереди закрашивают нарисованные ступеньки. За один ход можно закрасить не более двух ступенек. Выигрывает тот, кто закрасит последнюю ступеньку. Игра «Не больше двух предметов» *
Cлайд 6
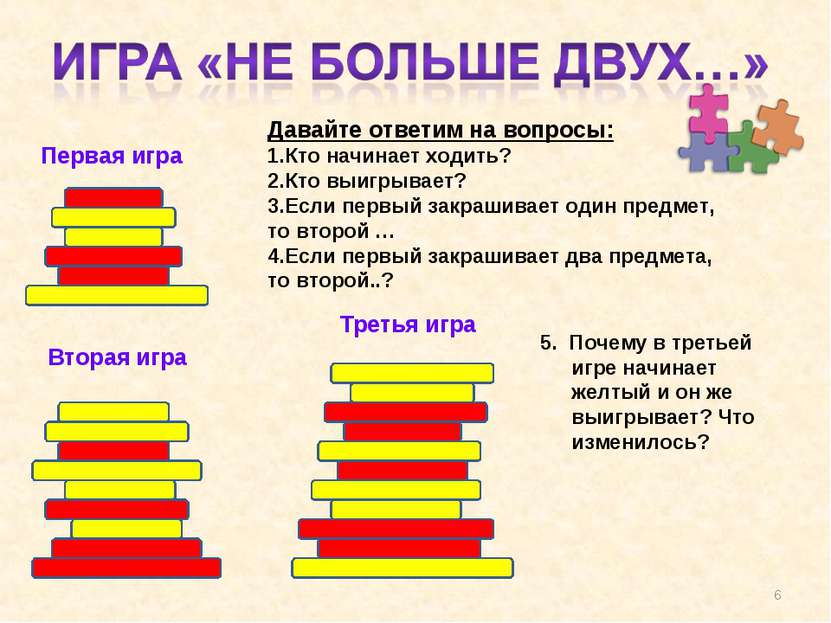
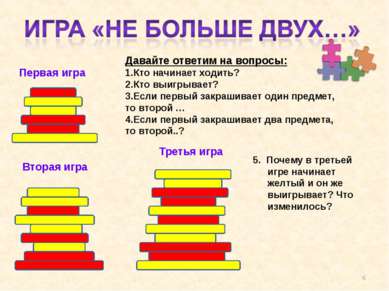Первая игра Давайте ответим на вопросы: Кто начинает ходить? Кто выигрывает? Если первый закрашивает один предмет, то второй … Если первый закрашивает два предмета, то второй..? Вторая игра Третья игра 5. Почему в третьей игре начинает желтый и он же выигрывает? Что изменилось? *
Cлайд 7
Правило 1. Перед началом игры раздели все предметы на группы ОТ КОНЦА К НАЧАЛУ. Кол-во предметов в группе определяется условиями (не больше 2, тогда группы по 3, т.е. (n+1)). Самая первая группа может оказаться неполной – эти предметы мы называем «лишними». Правило 2. Если есть «лишние» предметы, то выбери 1-ый ход и закрась «лишние» предметы. Если нет «лишних» предметов – то выбери второй ход. Правило 3. Дополняй ход другого игрока до (n+1) предмета, тогда в последней группе самый последний предмет будет ваш. *
Cлайд 8
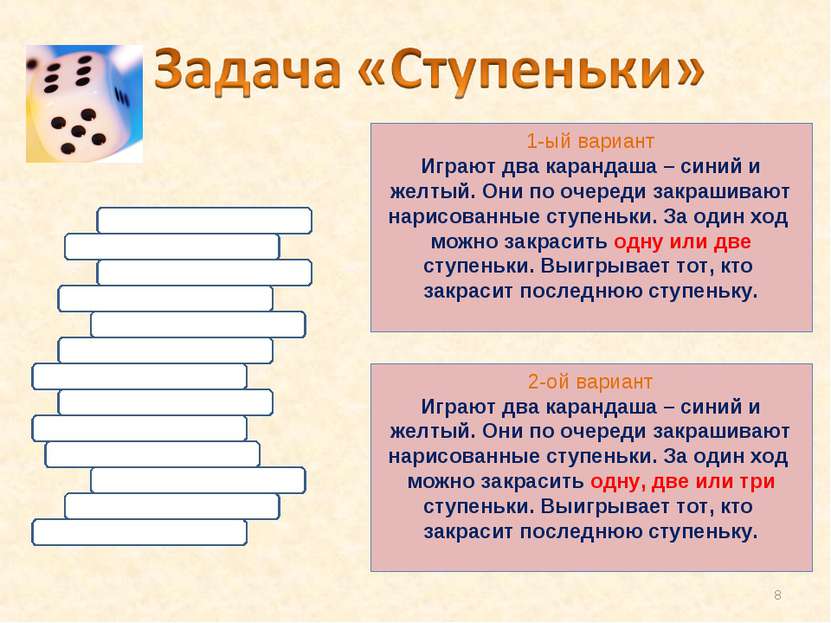
1-ый вариант Играют два карандаша – синий и желтый. Они по очереди закрашивают нарисованные ступеньки. За один ход можно закрасить одну или две ступеньки. Выигрывает тот, кто закрасит последнюю ступеньку. 2-ой вариант Играют два карандаша – синий и желтый. Они по очереди закрашивают нарисованные ступеньки. За один ход можно закрасить одну, две или три ступеньки. Выигрывает тот, кто закрасит последнюю ступеньку. *
Cлайд 9
У ромашки Вариант А) 12 лепестков; Вариант Б) 11 лепестков. За ход каждому игроку (всего их двое) разрешается сорвать либо один лепесток, либо два рядом растущих лепестка. Проигрывает игрок, который не сможет сделать ход. Как действовать второму игроку, чтобы выиграть независимо от ходов первого игрока? *
Cлайд 10
Имеются 2 кучи камней. Двое играющих берут по очереди камни. Разрешается взять один камень из любой кучи или по одному камню из обеих куч. Выигрывает взявший последние камни. При каком числе камней в кучах выиграет начинающий? На самом деле, задача аналогична игре «Не больше двух» подсказка *
Cлайд 11
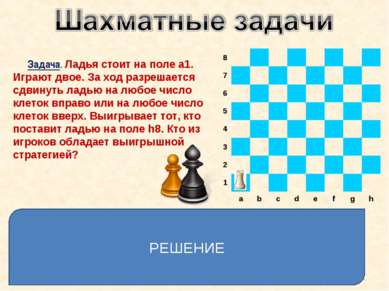Задача. Ладья стоит на поле a1. Играют двое. За ход разрешается сдвинуть ладью на любое число клеток вправо или на любое число клеток вверх. Выигрывает тот, кто поставит ладью на поле h8. Кто из игроков обладает выигрышной стратегией? Решение. Выигрышная стратегия есть у второго игрока: каждым ходом он может возвращать ладью на диагональ a1–h8. Первый игрок вынужден будет каждый раз уводить ладью с этой диагонали. Поскольку поле h8 принадлежит диагонали a1-h8, на него сумеет поставить ладью именно второй игрок. РЕШЕНИЕ * 8 7 6 5 4 3 2 1 a b c d e f g h
Cлайд 12
Двое играют на шахматной доске, передвигая по очереди одного короля. Допускаются ходы на одно поле влево, вниз или влево-вниз по диагонали. Выигрывает тот, кому удастся поставить короля на левый нижний угол. При каких начальных положениях короля выигрывает начинающий, а при каких – его соперник? * 8 7 6 5 4 3 2 1 a b c d e f g h
Cлайд 13
* Двое играющих по очереди (пропускать ход нельзя) выставляют на стол либо одну фишку, либо столько, сколько их уже стоит на столе, если нужное число фишек еще осталось в коробочке. Выигрывает тот, кто ставит последнюю фишку. В начале игры на столе фишек нет, а в коробочке: а) 5 фишек; б) 6 фишек; в) 7 фишек; г) 8 фишек. Кто выиграет, если будет играть наилучшим способом? Как должен ходить победитель?
Cлайд 14
В каких играх и задачах можно использовать выигрышную стратегию? Какие существуют правила выигрышной стратегии? Всегда ли в задачах указано, кто ходит первым? Назовите секреты выигрыша для игр «Не больше двух (трех) предметов». *
