X
Код презентации скопируйте его
Золотое сечение в искусстве
Скачать эту презентацию
Презентация на тему Золотое сечение в искусстве
Скачать эту презентациюCлайд 1
Золотое сечение в искусстве Выполнен учащейся 4 класса МОУ ДОД «Котовская детская школа искусств» Тамбовской области Поповой Еленой Руководитель –преподаватель Л.И.Аникеева Учебно-исследовательский проект
Cлайд 2
Тайну золотого сечения пытались осмыслить Платон, Евклид, Пифагор, Леонардо да Винчи, Кеплер и многие другие крупнейшие мыслители человечества. Они неразрывно связывали золотое сечение с понятием всеобщей гармонии, пронизывающей вселенную от микромира до макрокосмоса. Созданное давно Золотое сечение до сих пор волнует умы многих ученых. Целью данной работы является рассмотрение на обширном материале от античных времён до наших дней путей взаимодействия и взаимообогащения двух великих сфер человеческой культуры – науки (математики, биологии, анатомии) и искусства. Задачи исследования: изучение феномена «золотое сечение»; расширение представлений о сферах применения математики: показ фундаментальных закономерностей математики как формообразующими в архитектуре, поэзии, живописи, повседневной жизни и т.д.; осознание связи мира искусства и мира чисел; проведение эксперимента по интуитивному восприятию феномена золотого сечения; обобщение полученных данных. Материалом исследования послужили многочисленные публикации по теме, картины, скульптурные и архитектурные изображения, поэтические произведения.
Cлайд 3
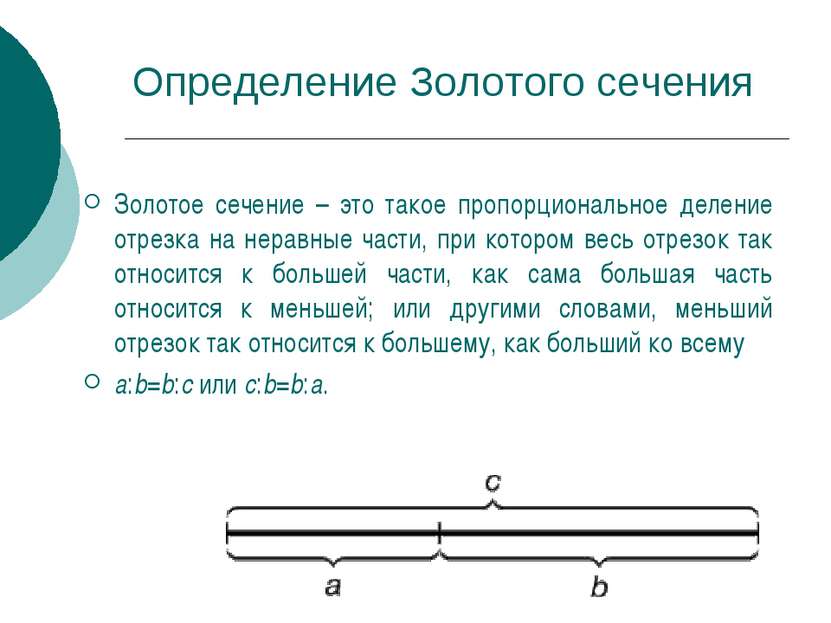
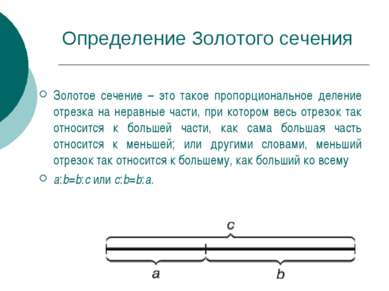Определение Золотого сечения Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему a:b=b:c или с:b=b:а.
Cлайд 4
Страницы истории Древнейшим литературным памятником, в котором встречается деление отрезка в отношении золотого сечения, являются «Начала» Евклида(3 век до н. э.) Но золотое сечение было известно и до Евклида. О нем знали Пифагор и его ученики (6 век до н. э.) Эта фигура – символ здоровья служила опо- знавательным знаком для пифагорийцев. К началу эпохи Возрождения усилился интерес к золотому сечению. Автором книги «Божественная пропорция» был крупнейший математик 15 века итальянец Лука Пачоли. Иллюстрировал книгу ве- ликий Леонардо да Винчи. Именно он ввел термин «золотое сечение». Оно обозначается через Ф по первой букве афинского скульптора Фидия.
Cлайд 5
Ряд Фибоначчи. С историей золотого сечения косвенным образом связано имя итальянского математика Фибоначчи. Ряд чисел 0,1,1,2,3,5,8,13,21,34,55 и т.д. известен как ряд Фибоначчи. Особенность последовательности чисел состоит в том что каждый её член, начиная с третьего, равен сумме двух предыдущих, а отношение смежных чисел ряда приближается к отношению золотого деления. Так 21:34=0,617, а 34:55=0,618. Любой человеческой деятельности присущи три отличительных особенности: форма и отношения, - и все они подчиняются суммационной последовательности Фибоначчи. Эллиотт
Cлайд 6
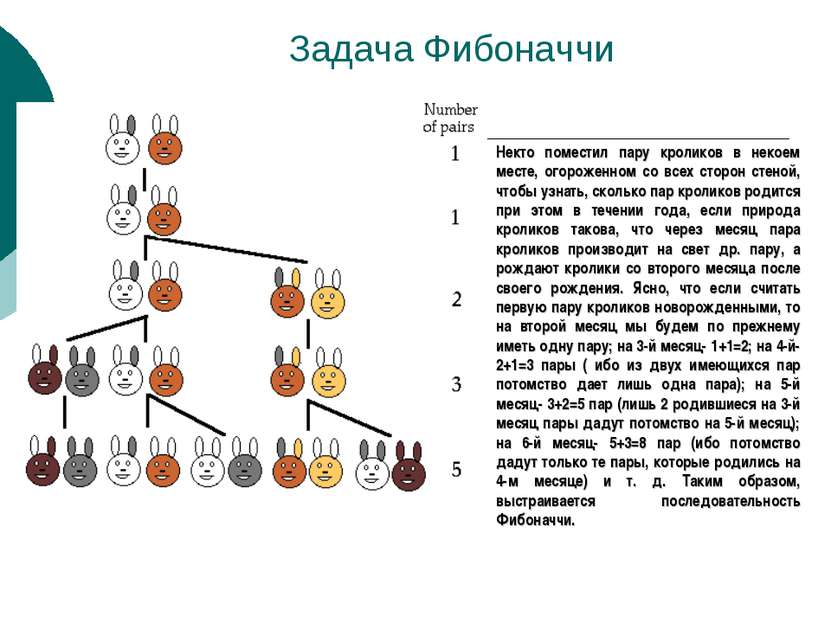
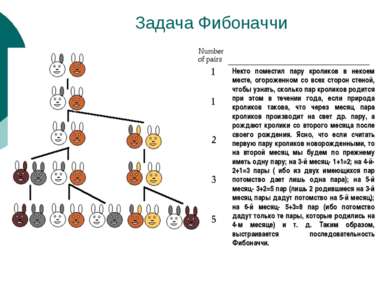Задача Фибоначчи Некто поместил пару кроликов в некоем месте, огороженном со всех сторон стеной, чтобы узнать, сколько пар кроликов родится при этом в течении года, если природа кроликов такова, что через месяц пара кроликов производит на свет др. пару, а рождают кролики со второго месяца после своего рождения. Ясно, что если считать первую пару кроликов новорожденными, то на второй месяц мы будем по прежнему иметь одну пару; на 3-й месяц- 1+1=2; на 4-й- 2+1=3 пары ( ибо из двух имеющихся пар потомство дает лишь одна пара); на 5-й месяц- 3+2=5 пар (лишь 2 родившиеся на 3-й месяц пары дадут потомство на 5-й месяц); на 6-й месяц- 5+3=8 пар (ибо потомство дадут только те пары, которые родились на 4-м месяце) и т. д. Таким образом, выстраивается последовательность Фибоначчи.
Cлайд 7
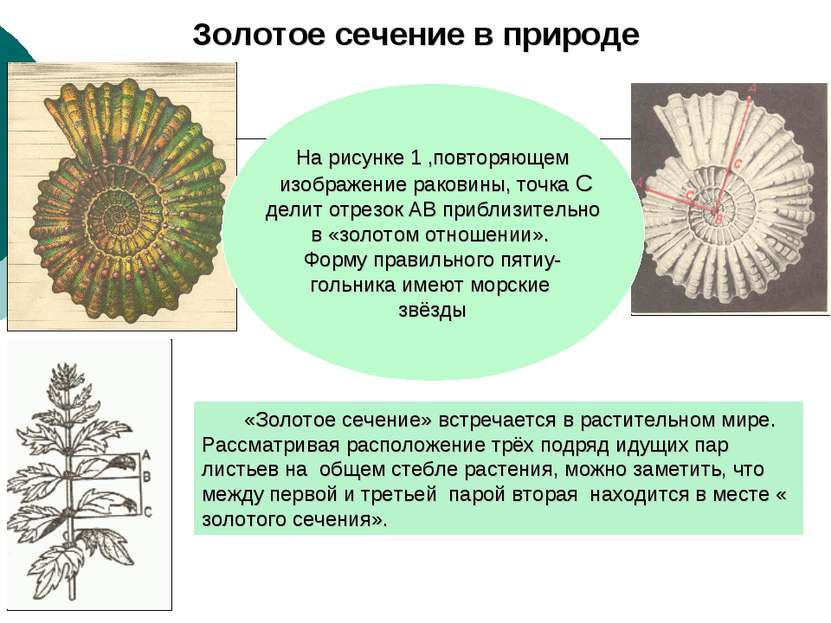
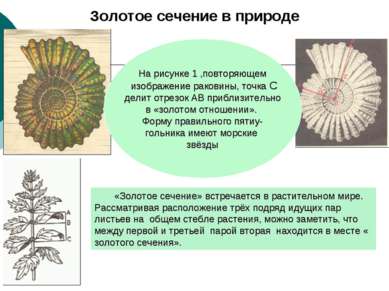Золотое сечение в природе «Золотое сечение» встречается в растительном мире. Рассматривая расположение трёх подряд идущих пар листьев на общем стебле растения, можно заметить, что между первой и третьей парой вторая находится в месте « золотого сечения». На рисунке 1 ,повторяющем изображение раковины, точка С делит отрезок АВ приблизительно в «золотом отношении». Форму правильного пятиу- гольника имеют морские звёзды
Cлайд 8
Золотое сечение в анатомии человеческого тела Сечение выражает среднестатистический закон : деление тела точкой пупа-один из основных показателей золотого сечения. Немецкий профессор Цейзинг в середине 18 столетия проделал огромную работу : он измерил более 2000 тел и высказал предположение , что золотые пропорции мужского тела колеблются в пределах среднего отношения 13:8=1,625. Пропорции золотого сечения проявляются и в отношении других частей тела – длина плеча , предплечья и кисти, кисти и пальцев и т. д. То,что части красиво сложенного человеческого тела находятся в определённой пропорции, знает каждый: недаром мы говорим о пропорционально сложенной фигуре
Cлайд 9
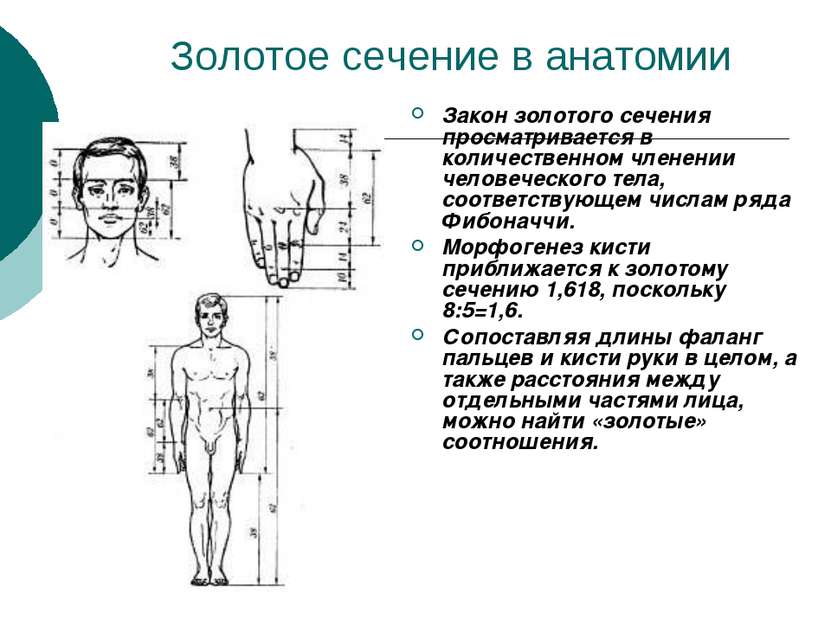
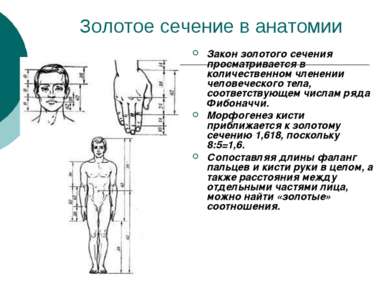Золотое сечение в анатомии Закон золотого сечения просматривается в количественном членении человеческого тела, соответствующем числам ряда Фибоначчи. Морфогенез кисти приближается к золотому сечению 1,618, поскольку 8:5=1,6. Сопоставляя длины фаланг пальцев и кисти руки в целом, а также расстояния между отдельными частями лица, можно найти «золотые» соотношения.
Cлайд 10
Сандро Ботичелли «Рождение Венеры» (около 1485 г). Пропорции Венеры выполнены в золотом сечении. «Поистине живопись – наука и законная дочь природы…» Леонардо да Винчи
Cлайд 11
Cлайд 12
Мона Лиза
Cлайд 13
И.И. Шишкин Наличие в знаменитой картине И.И. Шишкина «Сосновая Роща» ярких вертикалей и горизонталей, делящих её в отношении золотого сечения придаёт ей характер уравновешенности и спокойствия, в соответствии с замыслом художника.
Cлайд 14
Золотое сечение в архитектуре Одним из красивейших произведе-ний древнегреческой архитекту-ры является Парфенон (5 в. до н. э.) На рисунке виден целый ряд закономерностей, связанных с золотым сечением. Пропорции здания можно выразить через различные степени числа Ф=0,618… Золотое соотношение мы можем увидеть в здании собора Парижской Богоматери (Нотр-дам де Пари) В Смольном соборе в Санкт-Петербурге. В колокольне церкви Рождества Христова в Ярославле.
Cлайд 15
Здание бывшего сената в Москве
Cлайд 16
Пропорции в поэзии САПОЖНИК Картину раз высматривал сапожник И в обуви ошибку указал; Взяв тотчас кисть, исправился художник. Вот, подбочась, сапожник продолжал: «Мне кажется, лицо немного криво… А эта грудь не слишком ли нага?»… Тут Апеллес прервал нетерпеливо: «Суди, дружок, не свыше сапога!» Есть у меня приятель на примете: Не ведаю, в каком бы он предмете Был знатоком, хоть строг он на словах, Но черт его несет судить о свете: Попробуй он судить о сапогах!
Cлайд 17
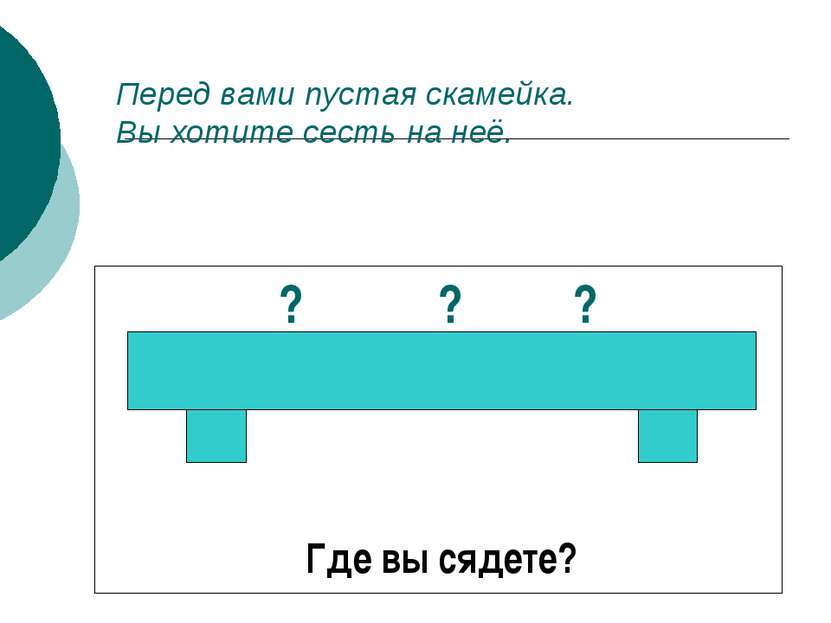
План действий Экспериментально-аналитическая часть: Выбор участников эксперимента. Проведение эксперимента. Анализ результатов измерений. Выводы.
Cлайд 18
Перед вами пустая скамейка. Вы хотите сесть на неё. ? ? ? Где вы сядете?
Cлайд 19
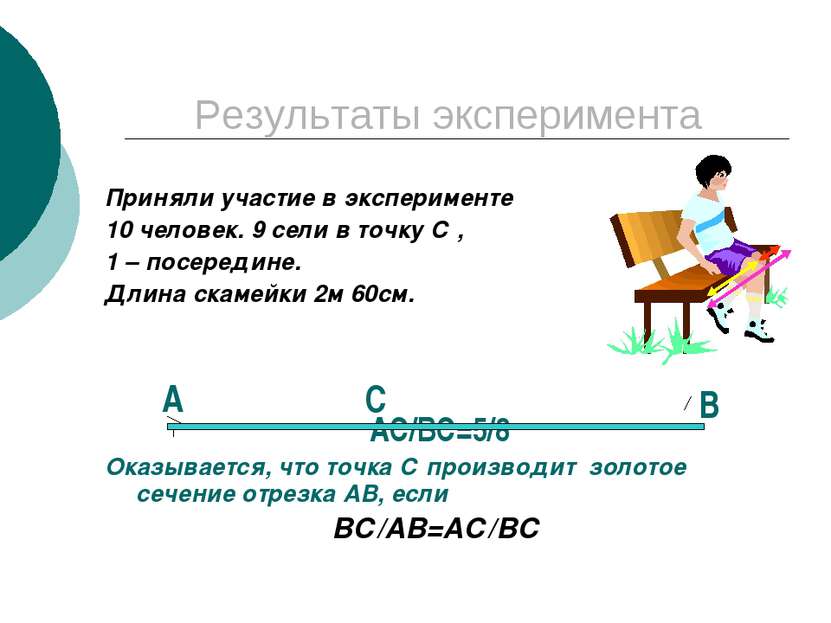
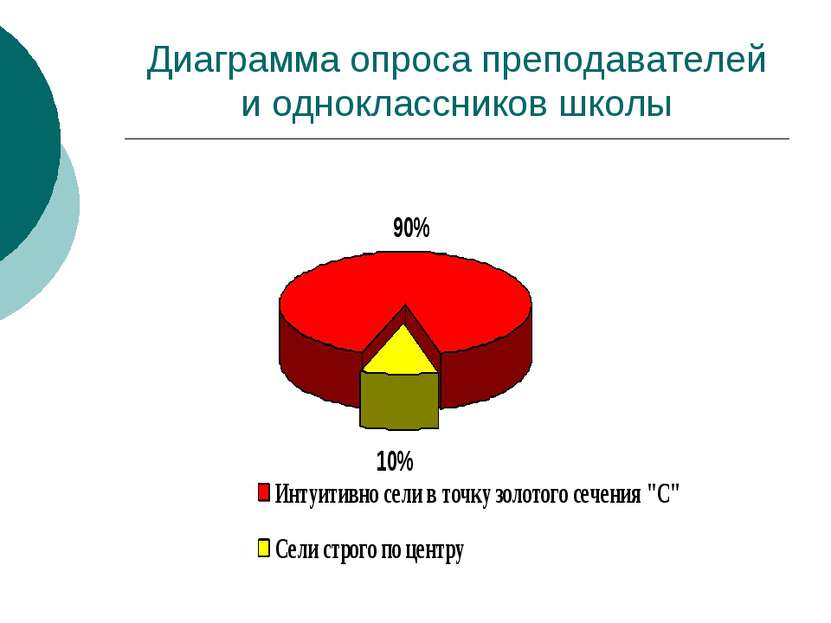
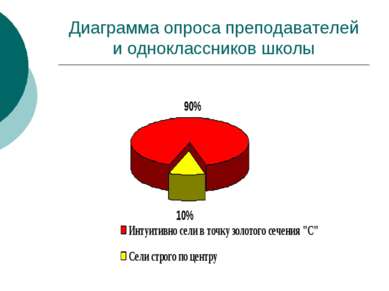
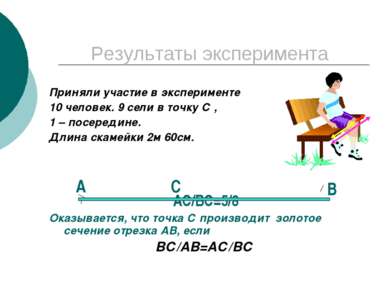Результаты эксперимента Приняли участие в эксперименте 10 человек. 9 сели в точку С , 1 – посередине. Длина скамейки 2м 60см. АС/ВС=5/8 Оказывается, что точка С производит золотое сечение отрезка АВ, если ВС/АВ=АС/ВС А С В
Cлайд 20
Диаграмма опроса преподавателей и одноклассников школы
Cлайд 21
В настоящей работе мы выявили основные математические истоки пропорции «золотого сечения» и способы ее воплощения в искусстве, культуре, науке.
Cлайд 22
Общие выводы В ходе работы я познакомилась с понятием «золотого сечения», гармоничными основами строения живого мира, классическими принципами построения в искусстве . Многие предметы неживой природы, представители живой природы, произведения искусства, отвечают принципам «золотого сечения».
Cлайд 23
Информационные ресурсы Список литературы: Азевич А. “Двадцать уроков гармонии” –М., “Школа-Пресс”, 1998 Васютинский Н. “Золотая пропорция” –М.,”Молодая гвардия”, 1990 Волошинов А.В. Математика и искусство. — М.: Просвещение, 1992. Гарднер М. “Математические головоломки и развлечения” –М., “Мир”, 1971 Гика М. Эстетика пропорций в природе и искусстве. — М.: Просвещение, 1986. Мороз О.И. В поисках гармонии. — М.: Атомиздат, 1978. Пидоу Д. “Геометрия и искусство” – М., “Мир”, 1989 Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение. — М.: Стройиздат, 1990. Энциклопедический словарь юного математика –М.,1989 Я познаю мир: Детская энциклопедия: Математика. — М.: АСТ, 1997
