X
Код презентации скопируйте его
Принцип Дирихле
Скачать эту презентацию
Презентация на тему Принцип Дирихле
Скачать эту презентациюCлайд 1
Принцип Дирихле Исполнитель: Амиева Анастасия ученица 10А класса МОУ СОШ № 128
Cлайд 2
Гипотеза: применение соответствующих формулировок принципа Дирихле – наиболее рациональный подход при решении задач. Наиболее применяема формулировка: "Если в n клетках сидят n + 1 "кроликов", то есть клетка, в которой не менее 2-х "кроликов " Цель: изучить, один из основных методов математики, принцип Дирихле
Cлайд 3
Объектом моего исследования является принцип Дирихле Предметом моего исследования является различные формулировки принципа Дирихле и их применение при решении задач Петер Густав Лежен Дирихле (13.2.1805 - 5.5.1859) - немецкий математик.
Cлайд 4
Этот принцип утверждает, что, если множество из N элементов разбито на п непересекающихся частей, не имеющих общих элементов, где N>n то, по крайней мере, в одной части будет более одного элемента Наиболее часто принцип Дирихле формулируется в одной из следующих форм: Если в n клетках сидят n + 1 "кроликов", то есть клетка, в которой не менее 2-х "кроликов"
Cлайд 5
Алгоритм применения принципа Дирихле Определить что в задаче является "клетками", а что — "кроликами" Применить соответствующую формулировку принципа Дирихле ?
Cлайд 6
У1. "Если в n клетках сидят не более n-1 "кроликов", то есть пустая клетка" У2. "Если в n клетках сидят n + 1 "кроликов", то есть клетка, в которой не менее 2-х "кроликов" " У3. "Если в n клетках сидят не более nk-1 "кроликов", то в какой-то из клеток сидят не более k-1 "кроликов " У4. "Если в n клетках сидят не менее n k+1 "кроликов", то в какой-то из клеток сидят не менее k+1 "кроликов""
Cлайд 7
У5. "Непрерывный принцип Дирихле. "Если среднее арифметическое нескольких чисел больше a, то, хотя бы одно из этих чисел больше a"; У6. "Если сумма n чисел меньше S, то по крайней мере одно из этих чисел меньше S/n". У7. "Среди p + 1 целых чисел найдутся два числа, дающие при делении на p один и тот же остаток".
Cлайд 8
Задача. В хвойном лесу растут 800000 елей. На каждой ели - не более 500000 иголок. Доказать, что существуют хотя бы две ели с одинаковым числом иголок. Научная классификация Царство: Растения Отдел: Голосеменные Класс: Хвойные Семейство: Сосновые Вид: Ели
Cлайд 9
Решение. Число "клеток" – 500000 (на каждой ели может быть от 1 иголки до 500000 иголок, 800000 ели – число "кроликов", так как, "кроликов" больше чем клеток, значит, есть "клетка", в которой сидит не менее двух "кроликов". Значит, существуют хотя бы две ели с одинаковым числом иголок. У2
Cлайд 10
Задача Количество волос на голове у человека не более 140 000 Доказать, что среди 150 000 человек найдутся 2 с одинаковым числом волос на голове Негроиды Монголоиды Европеоиды
Cлайд 11
Решение. Число "клеток" – 140 000 (у каждого человека может быть от 0 до 140 000), 150 000 человек – число "кроликов", так как, "кроликов" больше чем клеток, значит, есть "клетка", в которой сидит не менее двух "кроликов". Значит, существуют хотя бы два человека с одинаковым числом волос
Cлайд 12
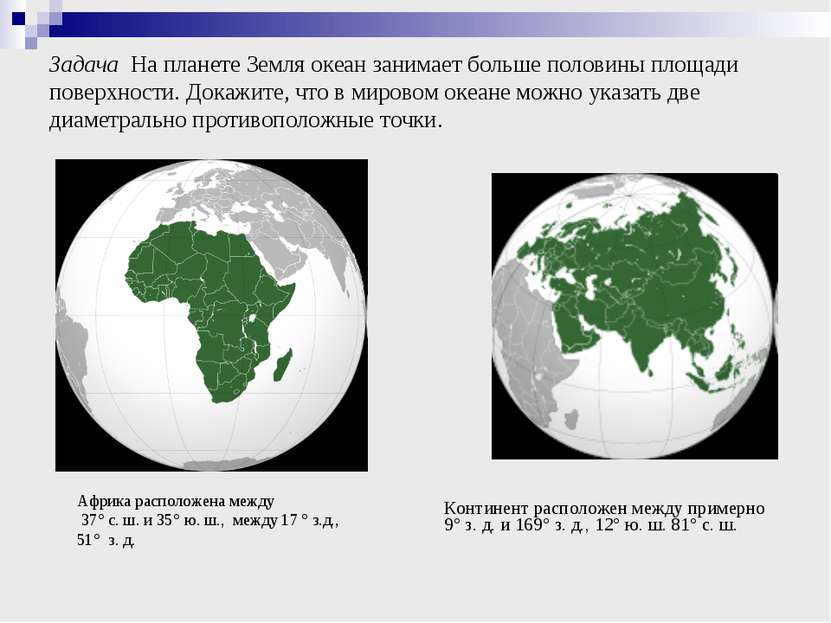
Задача На планете Земля океан занимает больше половины площади поверхности. Докажите, что в мировом океане можно указать две диаметрально противоположные точки. Континент расположен между примерно 9° з. д. и 169° з. д., 12° ю. ш. 81° с. ш. Африка расположена между 37° с. ш. и 35° ю. ш., между 17 ° з.д., 51° з. д.
Cлайд 13
Решение. Будем считать "кроликами" точки океана, а "клетками" - пары диаметрально противоположных точек планеты. Количество "кроликов" в данном случае - это площадь океана, а количество "клеток" - половина площади планеты. Поскольку площадь океана больше половины площади планеты, то "кроликов" больше, чем "клеток". Тогда есть "клетка", в которой сидит не менее двух "кроликов", т.е. пара противоположных точек, обе из которых - океан. У2
Cлайд 14
Геометрическая задача Внутри равнобедренной трапеции со стороной 2 расположено 4 точки. Доказать, что расстояние между некоторыми двумя из них меньше 1. Решение. Разобьем трапецию со стороной 2 на три треугольника со стороной 1. Назовем их "клетками", а точки – "кроликами". По принципу Дирихле из четырех точек хотя бы две окажутся в одном из трех треугольников. Расстояние между этими точками меньше 1, поскольку точки не лежат в вершинах треугольников
Cлайд 15
Задача на комбинаторику В коробке лежат шарики 4-х разных цветов (много белых, много черных, много синих, много красных). Какое наименьшее количество шариков надо наощупь вынуть из мешка, чтобы среди них заведомо оказались два одного цвета? Решение Возьмем за «кроликов» шары, а за «клетки» - черный, белый, синий, красный цвета. Клеток 4, поэтому если кроликов, хотя бы 5, то какие-то два попадут в одну клетку (будет 2 одноцветных шарика).
Cлайд 16
Задача на делимость Задача . Дано 11 различных целых чисел. Доказать, что из них можно выбрать два числа, разность которых делится на 10. Решение. По крайней мере, два числа из 11 дают одинаковый остаток при делении на 10 . Пусть это будут A = 10a + r и B = 10b + r. Тогда их разность делится на 10: A - B = 10(a - b).У2
Cлайд 17
Задача Дано n+1 различных натуральных чисел. Доказать, что из них можно выбрать два числа А и В, разность которых делится на n Задача Докажите, что среди n+1 различных натуральных чисел найдутся хотя бы два числа А и В такие что, число А2 - В2 делится на n. Докажем, что (А – B)(A+B) кратно n Задача Докажите, что среди n+1 различных натуральных чисел найдутся хотя бы два числа А и В такие что, число А3 – В3 делится на n. Докажем, что (А – B)(A2+AB +B2) кратно n
Cлайд 18
Задача Доказать, что число N5 оканчивается на ту же цифру, что число N Докажем, что N 5-N кратно 10 N(N-1) кратно 5 кратно 2
Cлайд 19
Малая теорема Ферма Если p - простое число, a - целое число, не делящееся на p, то a p-1 при делении на p даёт остаток 1 Доказательство Каждое из p - 1 чисел a, 2a, . . ., (p-1) a ("кроликов") даёт при делении на p ненулевой остаток (ведь a не делится на p) Пьер де Ферма (17 августа 1601) — 12 января 1665) — французский математик
Cлайд 20
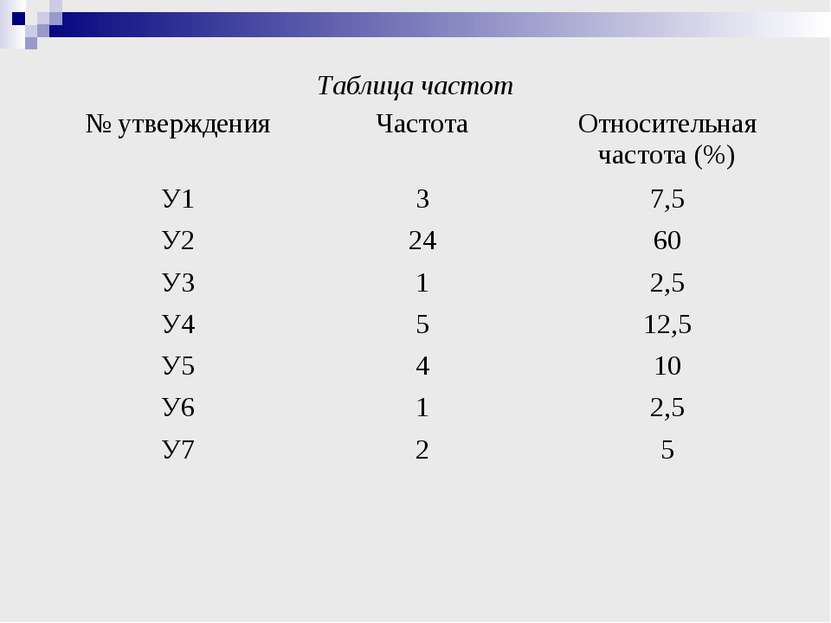
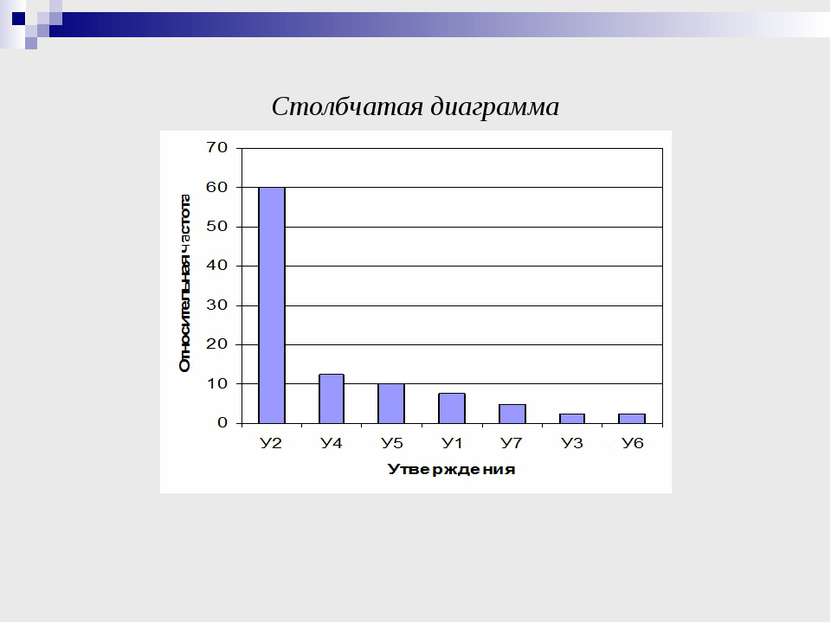
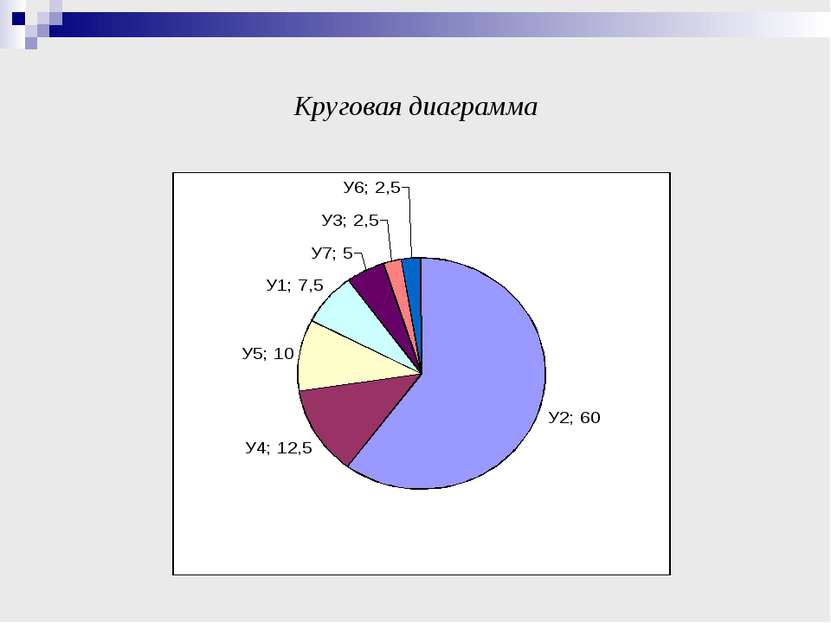
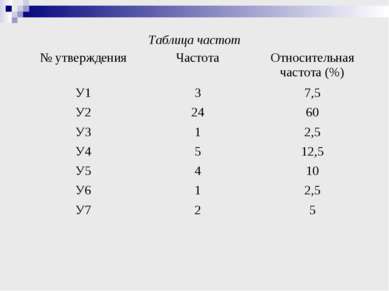
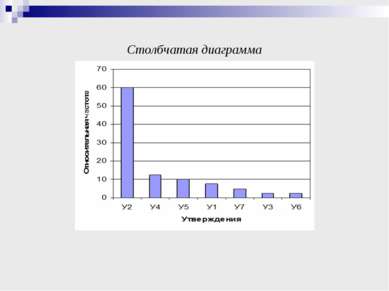
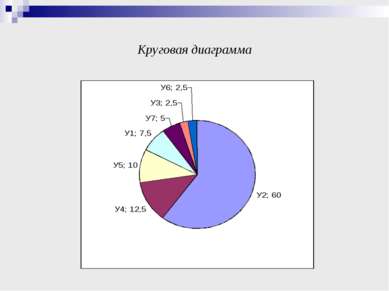
СТАТИСТИЧЕСКИЕ ИССЛЕДОВАНИЯ Упорядоченный ряд данных частоты использования утверждений при решении задач: 1 2 3 4 5 24 У3 У6 У7 У1 У5 У4 У2 Размах частот: 24 – 1 = 23, утверждение 2 при решении рассмотренных задач используется 24 раза, утверждения 3 и 6 один раз. Модой является утверждение 2, так как используется чаще других утверждений.
Cлайд 21
Таблица частот
Cлайд 22
Столбчатая диаграмма
Cлайд 23
Круговая диаграмма
Cлайд 24
Спасибо за внимание!
