X
Код презентации скопируйте его
Федерация водного поло Росссии
Скачать эту презентацию
Презентация на тему Федерация водного поло Росссии
Скачать эту презентациюCлайд 1
Федерация водного поло Росссии Материал: научная литература по исследованию операций, математической статистики и теории случайных процессов. Гипотеза: возможность использовать методы математической статистики для установления перспективности спортсменов, условий, наиболее благоприятных для тренировок, их эффективность.
Cлайд 2
Федоров Юрий, 11а класс, МОУ СОШ №91. Цель: привлечь внимание к возможности изучения многих ситуаций в спорте с математических позиций, и к целесообразности более обоснованных количественных и качественных оценок спортивных явлений. Методы исследования: сравнительный анализ и моделирование.
Cлайд 3
Задачи: 1. Распределение игровых амплуа в спортивной ватерпольной команде, обеспечивающее наибольший эффект в игре. 2. Составление для спортсменов диеты, удовлетворяющей требованиям медиков и, в то же время, наиболее экономной и сохраняющей вес спортсмена в определенных рамках. 3. Распределение между игроками команды обязанностей таким способом, чтобы общая результативность действий всей команды оказалась наибольшей. 4. Какое значение имеют броски в современном водном поло.
Cлайд 4
Актуальность Необходимость принимать решение возникает во многих спортивных ситуациях: в организации тренировок и соревнований, в комплектовании спортивных команд, в распределении обязанностей игроков команды, в выборе тактики игры и т. п.
Cлайд 5
Научная новизна Многочисленные ситуации столь сложны, а последствия принятых решений могут оказаться столь значительными, что предварительный количественный и качественный анализ становится обязательным. В этих случаях не обойтись без применения научных, в первую очередь математических, методов..
Cлайд 6
Задача1 Условия: ответственная встреча команды, новый тренер, замена ряда игроков. Перед новым тренером стоит задача: Распределить между игроками команды обязанности так, чтобы результативность команды оказалась наибольшей.
Cлайд 7
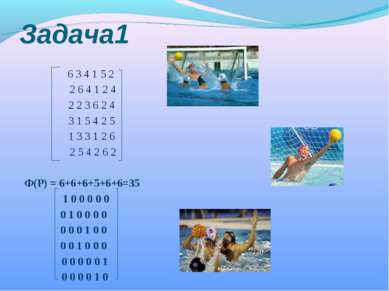Задача1 6 3 4 1 5 2 2 6 4 1 2 4 2 2 3 6 2 4 3 1 5 4 2 5 1 3 3 1 2 6 2 5 4 2 6 2 Ф(Р) = 6+6+6+5+6+6=35 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 1 0 0 0 0 1 0
Cлайд 8
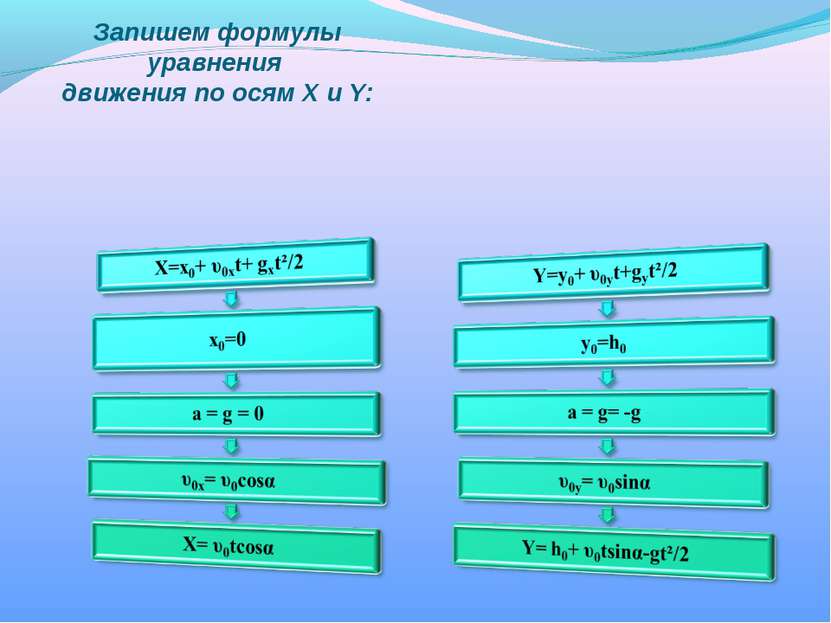
Задача2 Выведем уравнение движения мяча при броске по воротам. h0- высота с которой бросают мяч; L – расстояние от бросающего до ворот; g – ускорение свободного падения; υ0 – начальная скорость; υ 0х – проекция начальной скорости на оси Х; υ 0y – проекция начальной скорости на оси Y; α – угол броска над поверхностью воды; h=1,5м – высота от поверхности воды до ворот.
Cлайд 9
Запишем формулы уравнения движения по осям Х и Y:
Cлайд 10
Известно, что перекладина находится на высоте 1,5м над поверхностью воды.
Cлайд 11
Найдем L из t1 , где sinα > 0: L=x= υ0tcosα=υ0cosα(υ0sinα+√ υ0²sin²α-2g(1,5- h0))/g= (υ0²sinαcosα+υ0cosα√υ0²sin²α-2g(1,5- h0))/g; При h0=1,5 ; L= (υ0²sin2α)/g; Теперь найдем L из t2 , где sinα < 0: L=(υ0²sinαcosα+υ0cosα√υ0²sin²α-2g(1,5-h0))/g; При h0=1,5; L= (υ0²sin2α)/g.
Cлайд 12
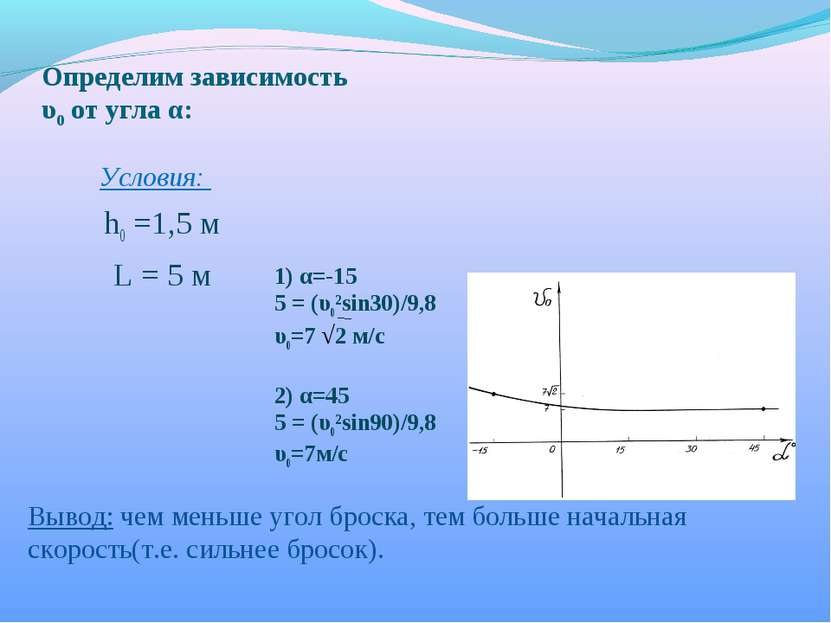
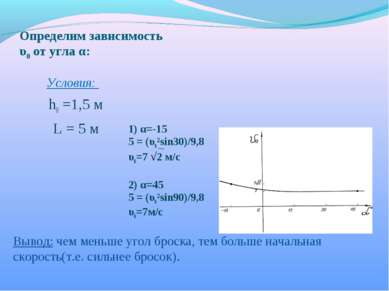Определим зависимость υ0 от угла α: Условия: h0 =1,5 м L = 5 м 1) α=-15 5 = (υ0²sin30)/9,8 υ0=7 √2 м/с 2) α=45 5 = (υ0²sin90)/9,8 υ0=7м/с Вывод: чем меньше угол броска, тем больше начальная скорость(т.е. сильнее бросок).
Cлайд 13
Задача3 Условия: Общие запасы питательного вещества βi , во всех видах продуктов составят сумму : Запасы питательных веществ β1 , β2 , …. , βn Различные продукты Z1, Z2 . . .., Zn ; a ij запасы (в некоторых единицах) питательного вещества вида βj в продукте Zij; стоимость некоторой единицы продукта С; минимальная норма питательного вещества bi ; количество продукта Xj; a i1 X1 + ... + a j1 Xj + ... + ainXm. a ijX1 + ... + a i j Xj + ... + ainXm. ≥ bi i = 1, ... , m (1) Общая стоимость приобретенных продуктов составит: F(X)= C1 * X1 +C 2 * X2 + ...+ Cn * Xn
Cлайд 14
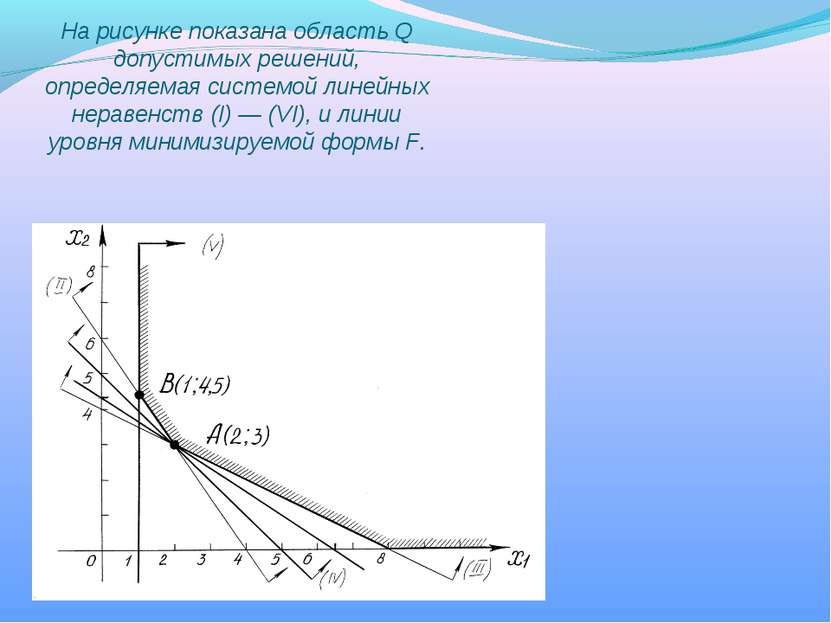
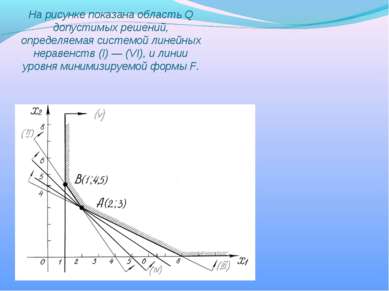
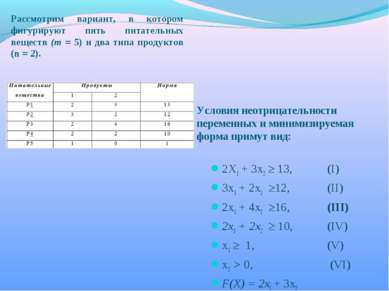Рассмотрим вариант, в котором фигурируют пять питательных веществ (т = 5) и два типа продуктов (n = 2). Условия неотрицательности переменных и минимизируемая форма примут вид: 2X1 + 3х2 ≥ 13, (I) Зх1 + 2х2 ≥12, (II) 2х1 + 4х2 ≥16, (III) 2х1 + 2х2 ≥ 10, (IV) x1 ≥ 1, (V) х2 > 0, (VI) F(X) = 2xl + 3х2
Cлайд 15
На рисунке показана область Q допустимых решений, определяемая системой линейных неравенств (I) — (VI), и линии уровня минимизируемой формы F.
