X
Код презентации скопируйте его
Движения
Скачать эту презентацию
Презентация на тему Движения
Скачать эту презентациюCлайд 1
Автор работы: Перчикова Антонина Васильевна
Cлайд 2
Движение – это отображение плоскости на себя, сохраняющее расстояние между точками.
Cлайд 3
Центральная симметрия Осевая симметрия Параллельный перенос Поворот
Cлайд 4
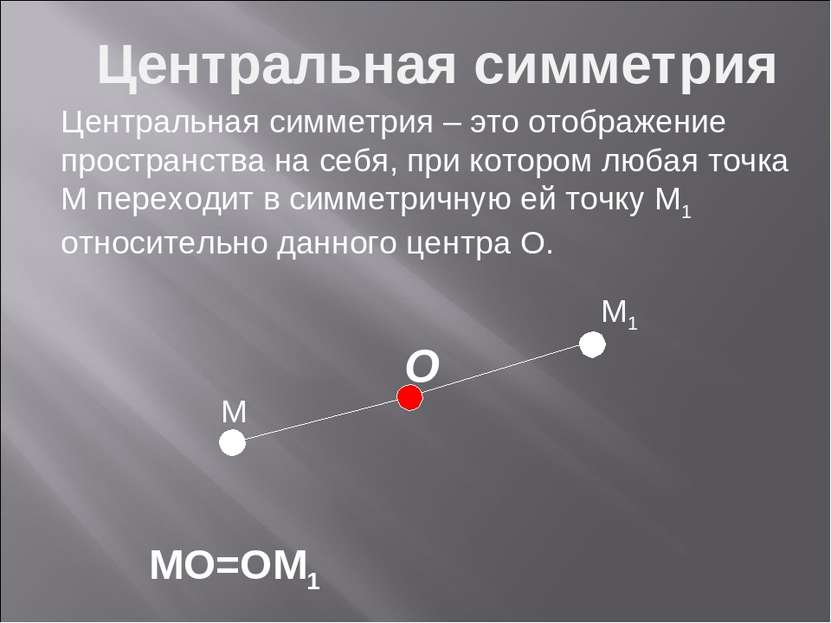
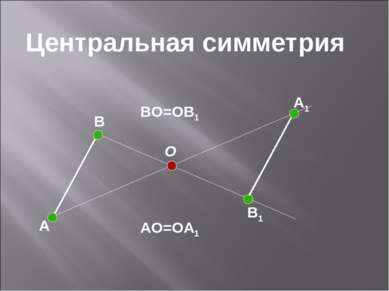
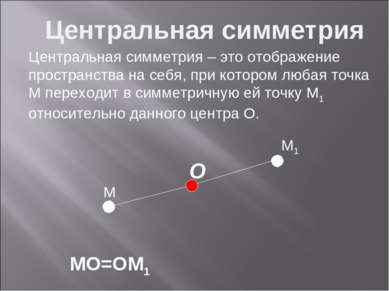M M1 MO=OM1 O Центральная симметрия Центральная симметрия – это отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно данного центра О.
Cлайд 5
A B O B1 A1 Центральная симметрия BO=OB1 AO=OA1
Cлайд 6
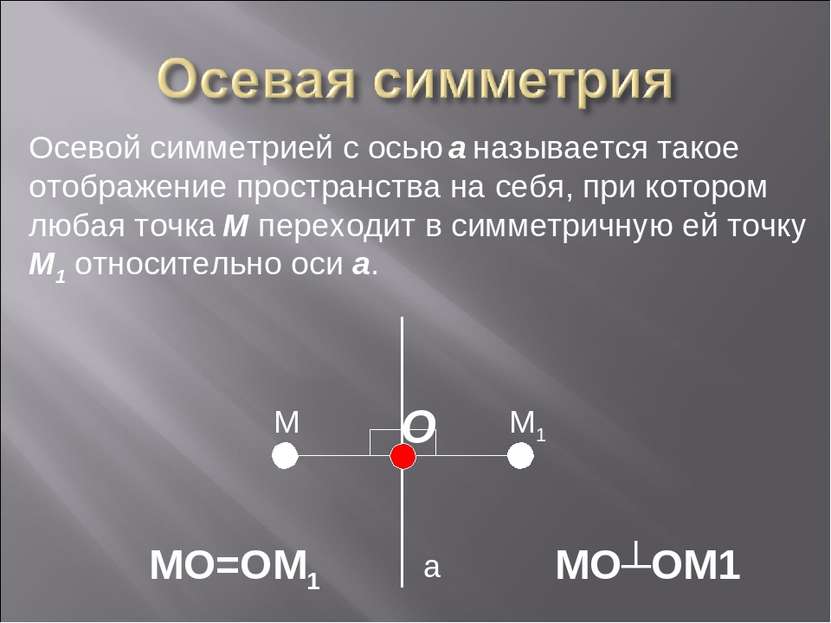
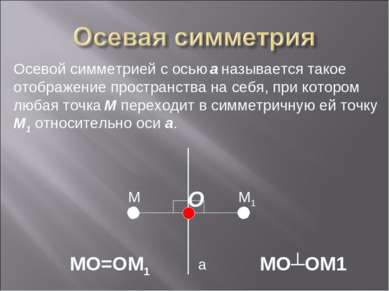а M M1 Осевой симметрией с осью а называется такое отображение пространства на себя, при котором любая точка М переходит в симметричную ей точку М1 относительно оси а. O MO=OM1 MO┴OM1
Cлайд 7
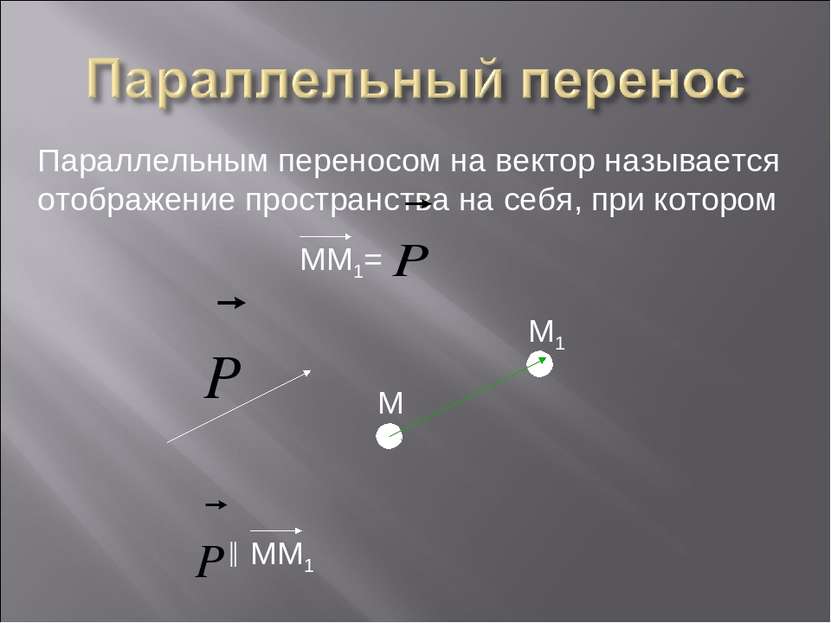
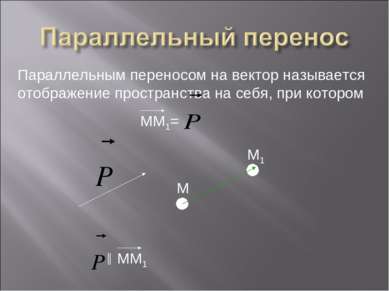Параллельным переносом на вектор называется отображение пространства на себя, при котором ММ1= M M1 ║ ММ1
Cлайд 8
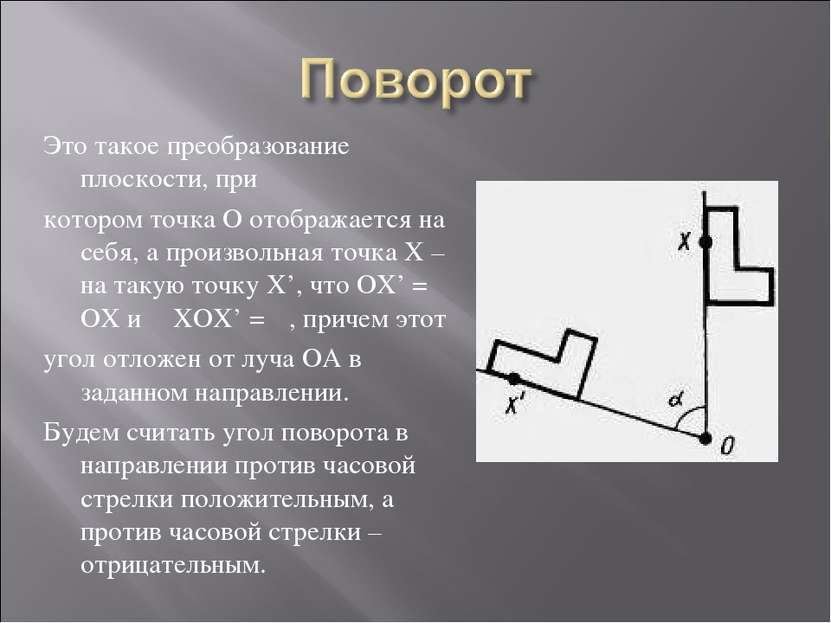
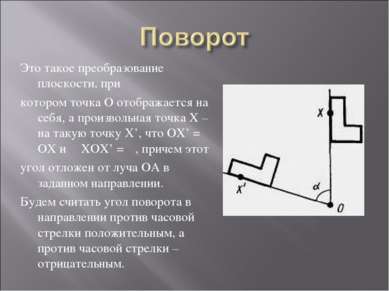Это такое преобразование плоскости, при котором точка О отображается на себя, а произвольная точка Х – на такую точку Х’, что ОХ’ = ОХ и ∠ХОХ’ = α, причем этот угол отложен от луча ОА в заданном направлении. Будем считать угол поворота в направлении против часовой стрелки положительным, а против часовой стрелки – отрицательным.
Cлайд 9
Cлайд 10
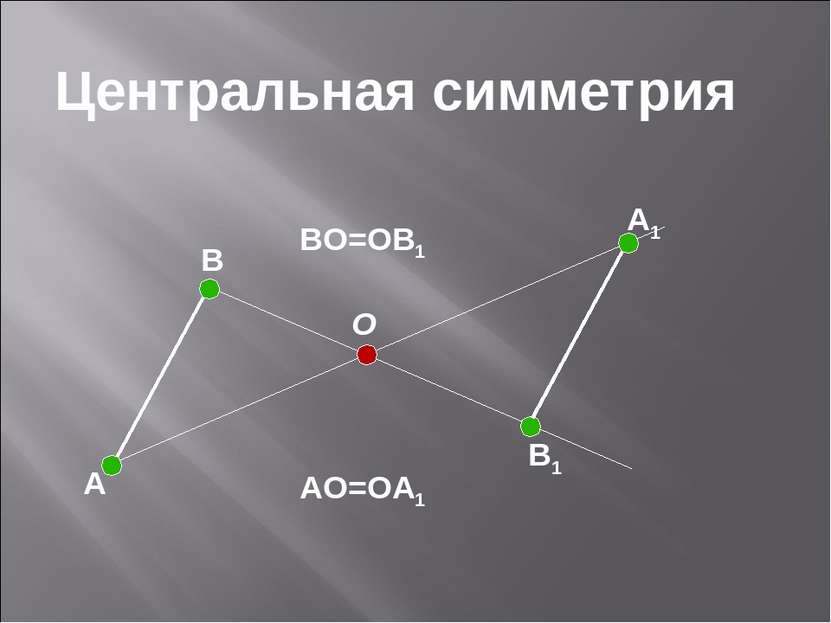
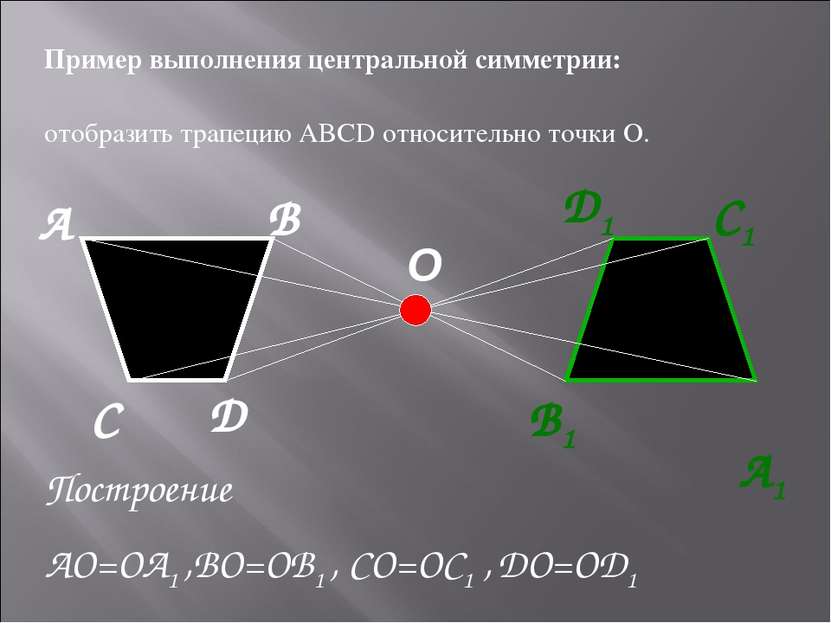
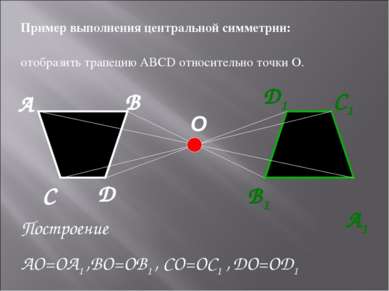O А B А1 D D1 C1 B1 C Пример выполнения центральной симметрии: отобразить трапецию ABCD относительно точки О. Построение AO=OА1 ,BO=OB1 , CO=OC1 , DO=OD1
Cлайд 11
http://images.yandex.ru/yandsearch?source=wiz&uinfo=sw-1263-sh-642-fw-1038-fh-448-pd-1&p=1&text=%D0%BF%D0%BE%D0%B2%D0%BE%D1%80%D0%BE%D1%82%20%D0%B2%20%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D0%B8&noreask=1&pos=41&rpt=simage&lr=18&img_url=http%3A%2F%2Fwww.lestnitza.ru%2Ffoto%2Flestnica%2Fp54_15.jpg http://images.yandex.ru/yandsearch?p=1&text=%D0%BE%D1%81%D0%B5%D0%B2%D0%B0%D1%8F%20%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F&pos=51&uinfo=sw-1263-sh-685-fw-1038-fh-479-pd-1&rpt=simage&img_url=http%3A%2F%2Fimg-fotki.yandex.ru%2Fget%2F21%2Fverasambros.20%2F0_efe3_2c226598_S http://ucheba-legko.ru/lections/viewlection/geometriya/9_klass/dvijeniya/parallelnyiy_perenos_i_povorot/lec_povorot http://images.yandex.ru/yandsearch?source=wiz&uinfo=sw-1263-sh-685-fw-1038-fh-479-pd-1&text=%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F%20%D0%B2%20%D0%BF%D1%80%D0%B8%D1%80%D0%BE%D0%B4%D0%B5&noreask=1&pos=7&lr=18&rpt=simage&img_url=http%3A%2F%2Fpsi.webzone.ru%2Fimg%2F111200.jpg http://images.yandex.ru/yandsearch?source=wiz&uinfo=sw-1263-sh-685-fw-1038-fh-479-pd-1&text=%D1%81%D0%B8%D0%BC%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F%20%D0%B2%20%D0%BF%D1%80%D0%B8%D1%80%D0%BE%D0%B4%D0%B5&noreask=1&pos=18&lr=18&rpt=simage&img_url=http%3A%2F%2Fimg-fotki.yandex.ru%2Fget%2F51%2Ftaurus-foto.11%2F0_17453_97332ec8_XL
