X
Код презентации скопируйте его
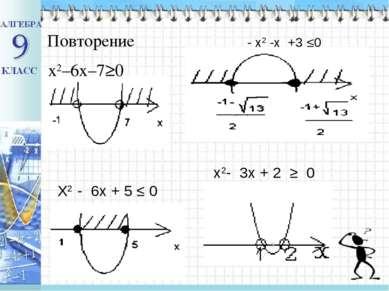
Метод интервала
Скачать эту презентацию
Презентация на тему Метод интервала
Скачать эту презентациюCлайд 1
Решение неравенств методом интервалов МБОУ ООШ №21 х. Ханькова Коломиец Лилия Геннадьевна, учитель математики урок алгебры в 9 классе
Cлайд 2
Цели урока: 1.Образовательная: Продолжить формирование системы знаний о способах решения неравенств второй степени различными способами. 2.Воспитательная: Формировать навыки общения, умения работать в коллективе. 3.Развивающая: Продолжить совершенствование навыков самостоятельной поисковой деятельности. Задачи урока: 1. Отработать навыки алгоритма решения квадратных неравенств с учащимися. 2. Отработать навыки и умения решать неравенства методом интервалов по алгоритму.
Cлайд 3
Оборудование: Стенд текстовых заданий Листы результатов Алгебра-9 под ред.С.А. Теляковского. М, « Просвещение», 2011г. Математика 9 класс подготовка к ГАИ 9 класс под ред. Ф.Ф.Лысенко 2013г. Математика 9 класс ГИА 2015 50 тестов под ред. Д.А.Мальцева
Cлайд 4
Cлайд 5
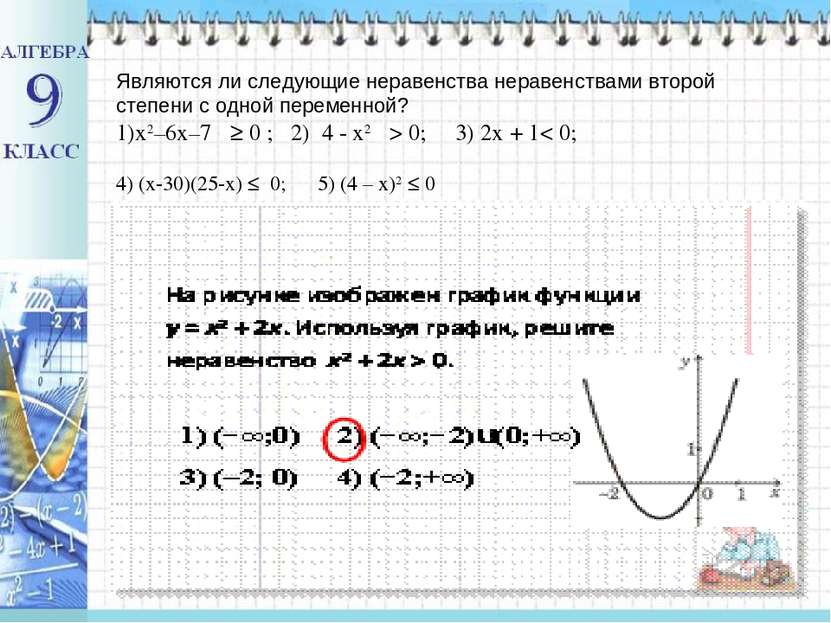
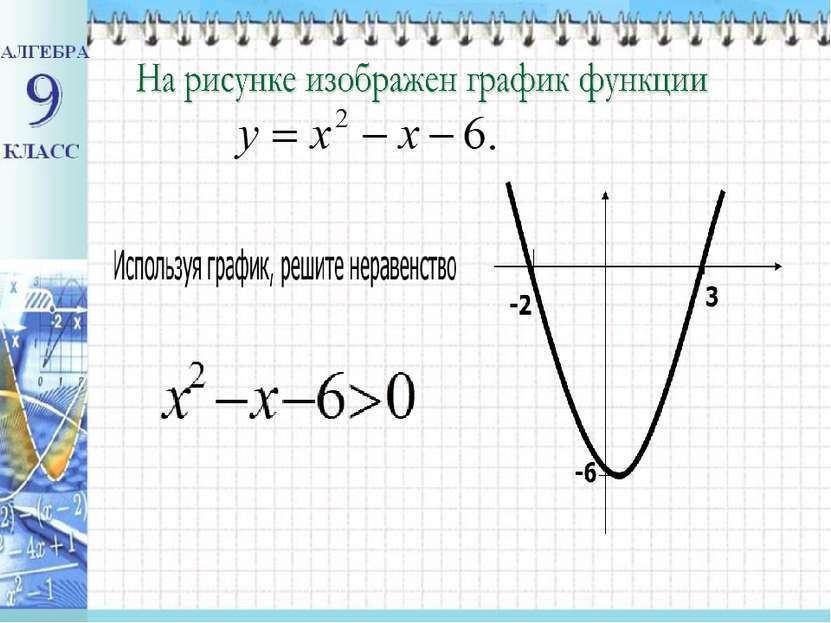
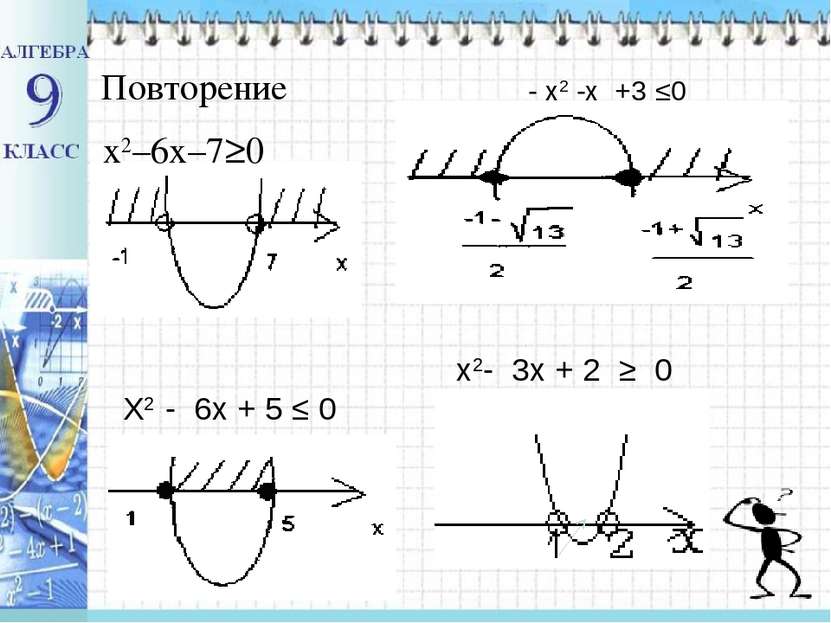
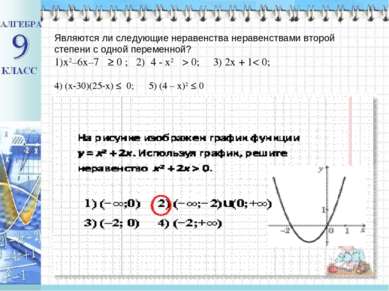Являются ли следующие неравенства неравенствами второй степени с одной переменной? x2–6x–7 ≥ 0 ; 2) 4 - x2 > 0; 3) 2х + 1< 0; 4) (х-30)(25-х) ≤ 0; 5) (4 – x)2 ≤ 0
Cлайд 6
Cлайд 7
x2–6x–7≥0 - х2 -х +3 ≤0 Х2 - 6х + 5 ≤ 0 х2- 3х + 2 ≥ 0 Повторение
Cлайд 8
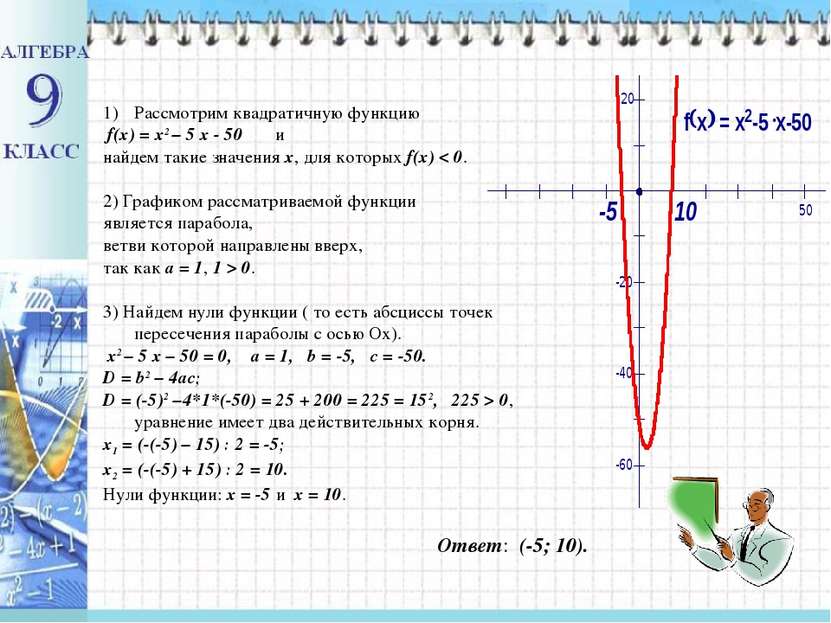
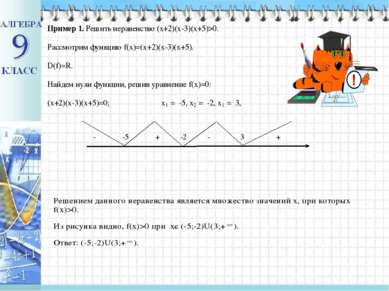
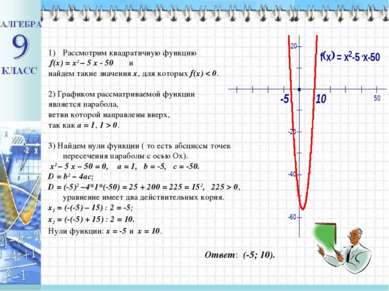Рассмотрим квадратичную функцию f(x) = x2 – 5 x - 50 и найдем такие значения x, для которых f(x) < 0. 2) Графиком рассматриваемой функции является парабола, ветви которой направлены вверх, так как a = 1, 1 > 0. 3) Найдем нули функции ( то есть абсциссы точек пересечения параболы с осью Ox). x2 – 5 x – 50 = 0, a = 1, b = -5, c = -50. D = b2 – 4ac; D = (-5)2 –4*1*(-50) = 25 + 200 = 225 = 152, 225 > 0, уравнение имеет два действительных корня. x1 = (-(-5) – 15) : 2 = -5; x2 = (-(-5) + 15) : 2 = 10. Нули функции: x = -5 и x = 10. Ответ: (-5; 10).
Cлайд 9
Алгоритм решения неравенств второй степени с одной переменной 1.Приведите неравенство к виду ax2+bx+c>0 (ax2+bx+c0 (y0 (y
Cлайд 10
Метод интервалов Метод интервалов Выбираем промежутки, в которых f(x) < 0: это выполняется для всех –5 < х < 10. Ответ: (-5; 10).
Cлайд 11
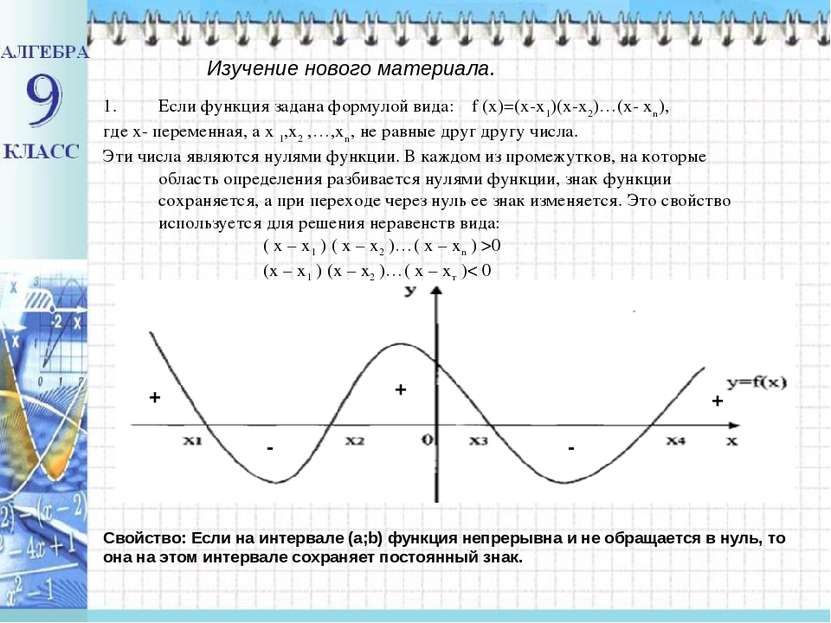
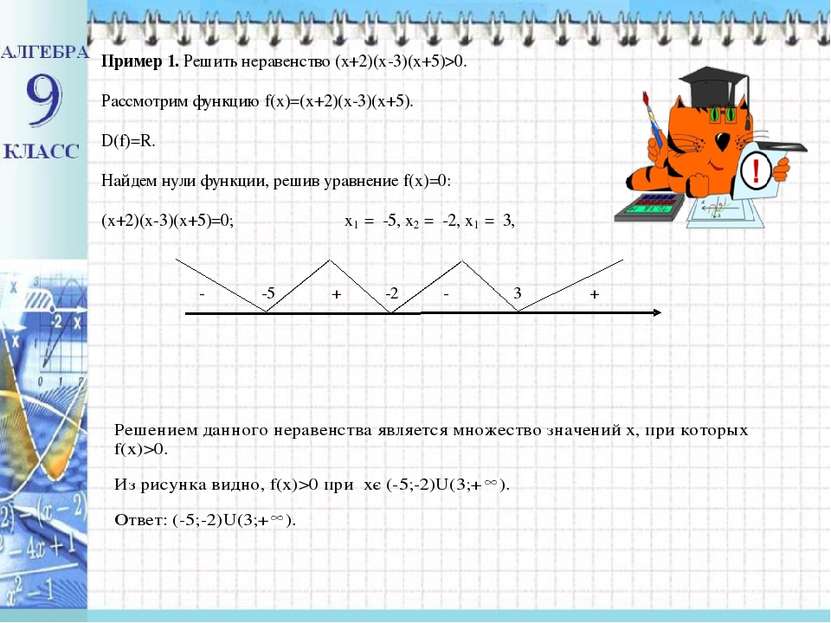
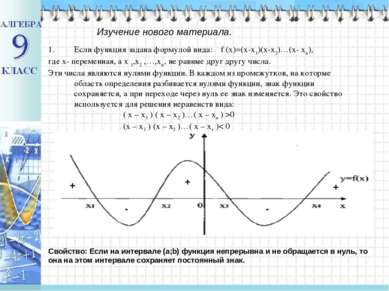Если функция задана формулой вида: f (x)=(x-x1)(x-x2)…(x- xn), где х- переменная, а х 1,х2 ,…,хn, не равные друг другу числа. Эти числа являются нулями функции. В каждом из промежутков, на которые область определения разбивается нулями функции, знак функции сохраняется, а при переходе через нуль ее знак изменяется. Это свойство используется для решения неравенств вида: ( х – х1 ) ( х – х2 )…( х – хn ) >0 (x – x1 ) (x – x2 )…( x – xт )< 0 Изучение нового материала. Свойство: Если на интервале (а;b) функция непрерывна и не обращается в нуль, то она на этом интервале сохраняет постоянный знак. + + + - -
Cлайд 12
Cлайд 13
Cлайд 14
2 .При решении неравенств широко используется разложение на множители а2 – в2 =(а - в)( а – в ) а2 + 2ав + в2 = (а + в)2 а2 – 2ав + в2 =(а – в)2 ах2 +вх +с = а (х – х1)(х – х2)
Cлайд 15
Проверь своё решение 5 - 4 + + - Ответ: Решение. Решить неравенство (x – 5)(x + 4)(x + 5) ≤ 0 f(x) = (x – 5)(x + 4)(x + 5) Нули функции x = 5, x= - 4, x = - 5 - 5 - (- ∞;-5} U [-4; 5]
Cлайд 16
Решите методом интервалов неравенства: 2) 1) x(x + 2)(x – 1) ≥ 0 Давайте закрепим ! (x – 1)(3 – x) (x – 2) ≤ 0
Cлайд 17
Оценка работы в парах За каждый верно заполненный пропуск – поставьте 1 балл. 6 - 7 баллов – удовлетворительно, «3». 8 - 9 баллов – хорошо, «4». 10-11 баллов – отлично, «5». 0 - 5 баллов – незачтено !
Cлайд 18
Cлайд 19
Решите неравенство: 5) (х-4)(х+7)(х-6)0 7) 8)
Cлайд 20
Работа в группах 9) (х-1)(х+4) ≤ 0. 10) (х+2)(х-5) ≤ 0. 11) (х-6)(х-4) > 0. · [-4;1],(-3;1),[0;1],(-4;1),[-4;-2] [-2;-5],(2;5),[0;2],[-1;2),[3;-5] (7;10),[-5;3],[8;11),[-6;4),[-7;0) Определить промежуток , который принадлежит неравенству
Cлайд 21
Проверь своё решение
Cлайд 22
Физкультминутка Расслабимся не отходя от математики: 1. Покажите направление ветвей параболы, если старший коэффициент параболы а>0 ,а
Cлайд 23
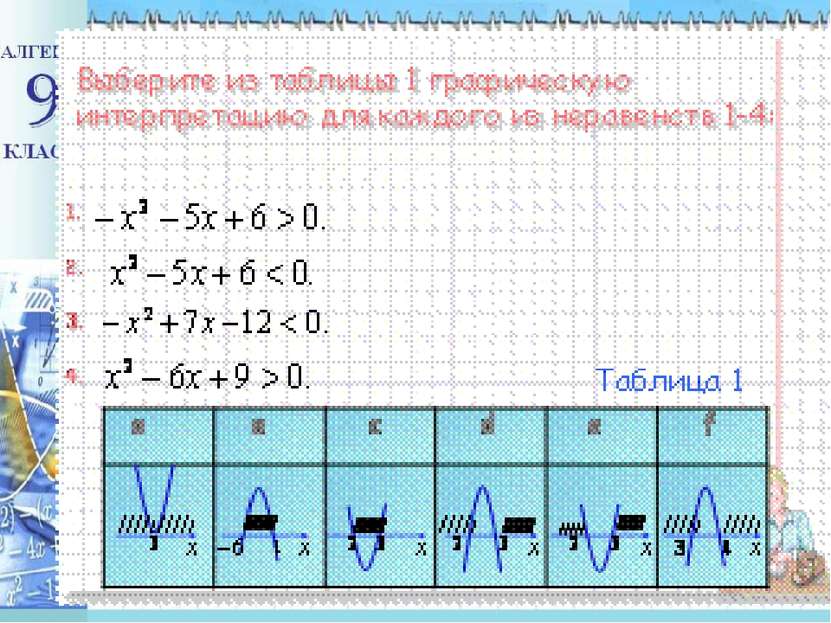
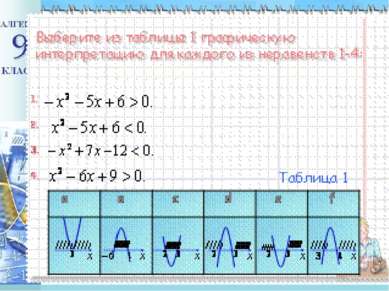
№ п/п № задания Ответы Баллы 1 - Х2 - 5Х + 6 > 0 2 2 Х2 - 5Х + 6 < 0 3 3 - Х2 + 7Х - 12 < 0 6 4 Х2 - 6Х + 9 > 0 1 5 (х-4)(х+7)(х-6)0 (-5;1) ᴜ ( 9; +∞) 7 (-∞ ; -2] ᴜ [3 ; +∞ ) 8 (-∞ ; - 1,5] ᴜ [6 ; +∞ ) 9 (х-1)(х+4) ≤ 0 [-4; -2], [-4; 1], [0; 1] 10 (х+2)(х-5) ≤ 0 [0; 2] 11 (х-6)(х-4) > 0 [-5; 3], [-6; 4) 12 Х2 - 3Х - 4 ≥ 0 b 13 Х2 - 3Х - 10 < 0 a
Cлайд 24
1) §15 (глава II) Домашнее задание. 2) №325 (а, б) 3) Повторение № 306(г;в)
Cлайд 25
Рефлексия. 1.Что вы ожидали от работы на данном уроке? Сравните свои предварительные цели и реально достигнутые результаты. 2. Какие чувства и ощущения возникали у вас в ходе работы? Что оказалось для вас самым неожиданным? 3. Что вам более всего удалось, какие моменты были выполнены наиболее успешно? 4. Перечислите основные трудности, которые вы испытывали во время урока. Как вы их преодолевали?
Cлайд 26
Использованные источники Учебник: Алгебра-9 класс, Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, М.: Просвещение, 2011. 2. Рурукин А.Н., Полякова С.А., Поурочные разработки по алгебре: 9 класс. – М.: ВАКО, 2010 – (В помощь школьному учителю). 3. Для создания шаблона презентации использовалась картинка http://www.box-m.info/uploads/posts/2009-04/1238954029_1.jpg и шаблон с сайта http://aida.ucoz.ru 4. Изображение кота http://s39.radikal.ru/i084/1008/34/683cd4886d3f.jpg
