X
Код презентации скопируйте его
Графы и их применение (11 класс)
Скачать эту презентацию
Презентация на тему Графы и их применение (11 класс)
Скачать эту презентациюCлайд 1
Живаева Екатерина Ученица 11 класса
Cлайд 2
Cлайд 3
Выяснить особенности применения теории графов при решении задач и в практической деятельности.
Cлайд 4
- изучить теорию графов; - решить задачи с помощью графов; - рассмотреть применение теории графов в различных областях науки; - разработать оптимальный вариант ремонта кухни с помощью сетевого графика; - составить генеалогическое древо.
Cлайд 5
Родоначальником теории графов принято считать математика Леонарда Эйлера(1707-1783). Он предложил изящное решение знаменитой задачи о 7 Кенигсбергских мостах в 1736 году, а также придумал общий метод решения подобных задач.
Cлайд 6
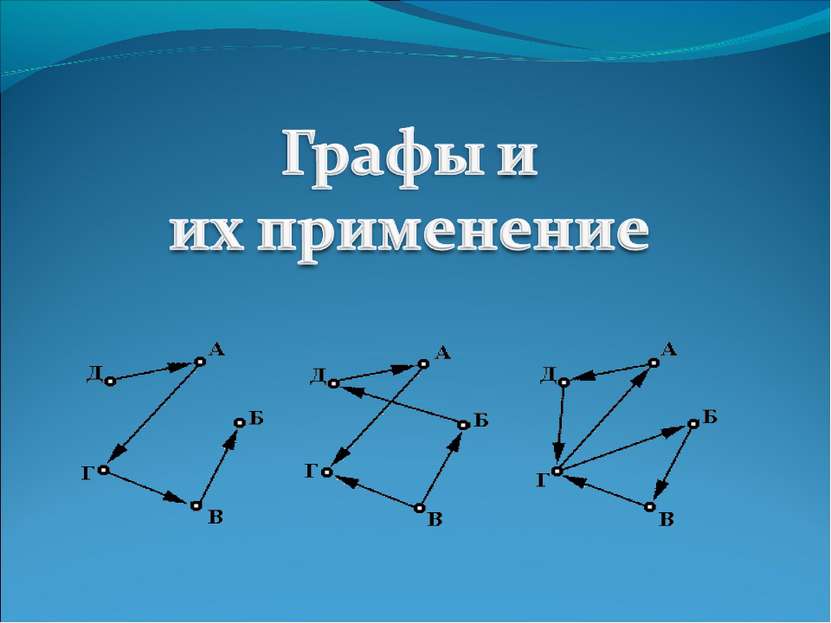
Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек. Теория графов - раздел математики, особенность которого геометрический подход к изучению объектов.
Cлайд 7
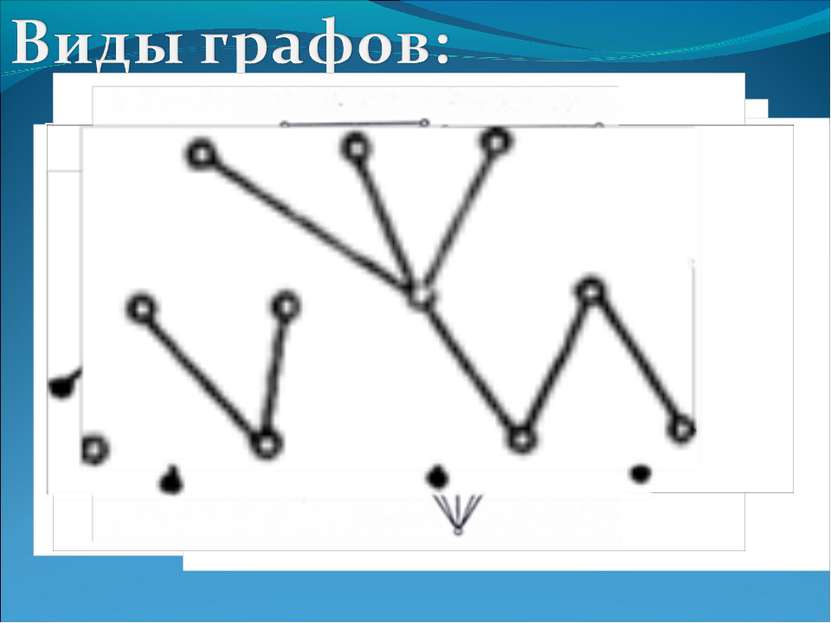
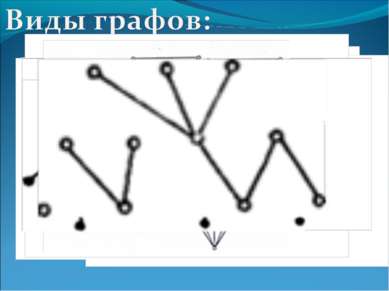1) Нулевой граф 2) Неполный граф 3) Полный граф 4) Несвязный граф 5) Связный граф 6) Ориентированный граф (орграф) 7) Взвешенный граф 8) Эйлеровый граф 9) Плоский граф 10) Дерево 11) Лес
Cлайд 8
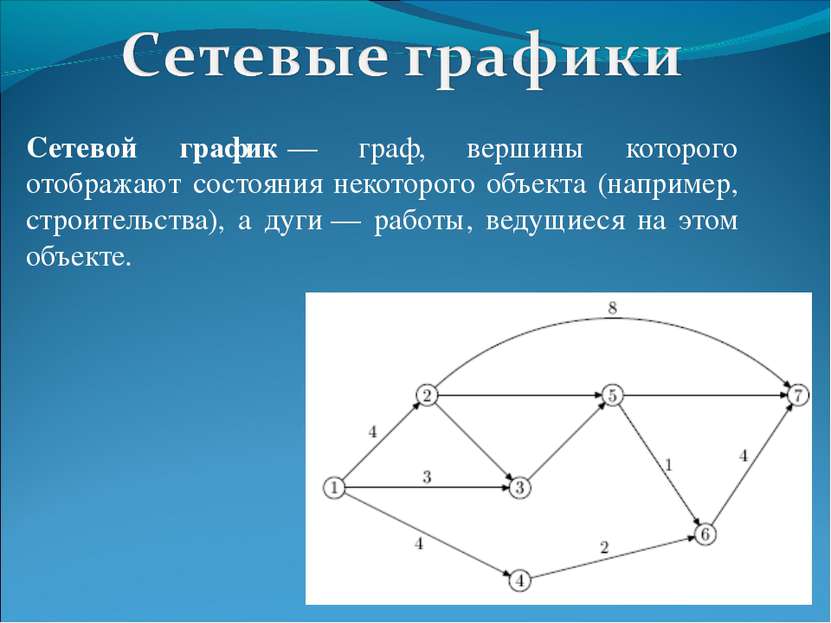
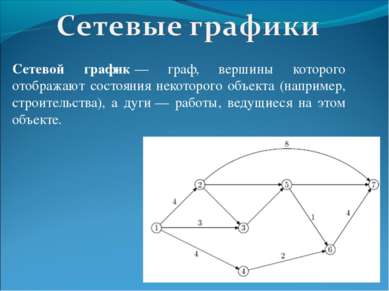Сетевой график — граф, вершины которого отображают состояния некоторого объекта (например, строительства), а дуги — работы, ведущиеся на этом объекте.
Cлайд 9
1) В теории информации 2) В биологии 3) В химии 4) В физике 5) На транспорте
Cлайд 10
Я составила три варианта ремонта кухни с помощью сетевых графиков № Операция Время (дни) 1 Уборка мебели, расчистка территории 1 2 Укладка плитки на стены 1 3 Закрепление ПВХ панелей на потолке 1 4 Клейка обоев, замазывание щелей между плитками 2 5 Крепление уголков на потолке, замена розеток 1 6 Укладка линолеума, закрепление плинтусов 1 7 Уборка, расстановка мебели 1
Cлайд 11
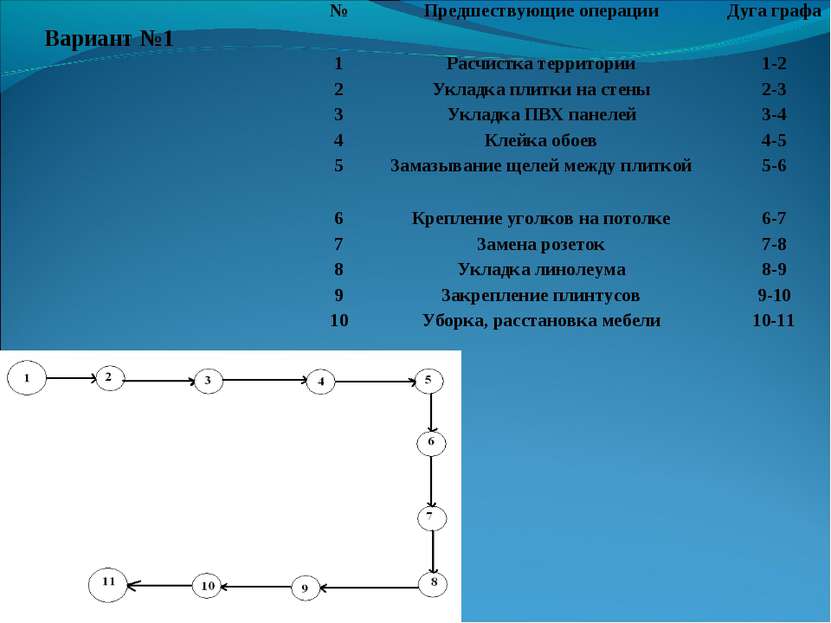
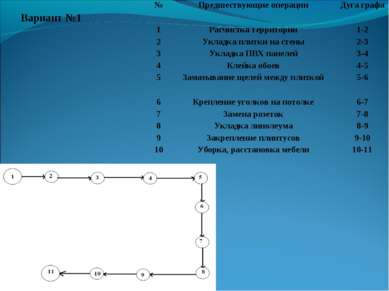Вариант №1 № Предшествующие операции Дуга графа 1 Расчистка территории 1-2 2 Укладка плитки на стены 2-3 3 Укладка ПВХ панелей 3-4 4 Клейка обоев 4-5 5 Замазывание щелей между плиткой 5-6 6 Крепление уголков на потолке 6-7 7 Замена розеток 7-8 8 Укладка линолеума 8-9 9 Закрепление плинтусов 9-10 10 Уборка, расстановка мебели 10-11
Cлайд 12
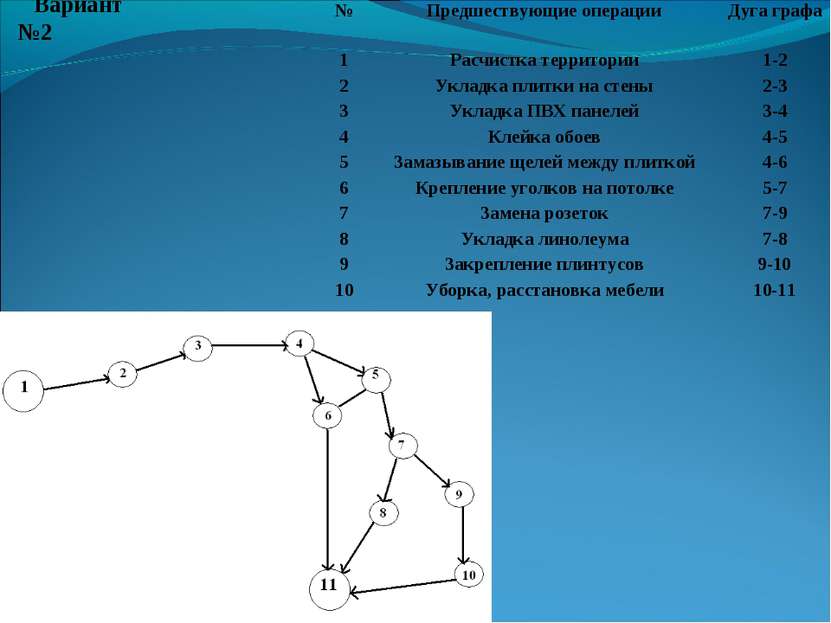
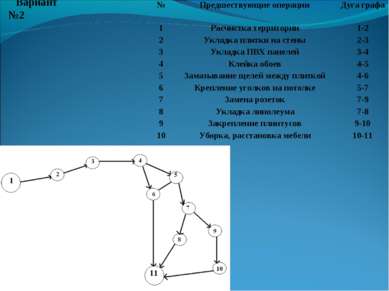Вариант №2 № Предшествующие операции Дуга графа 1 Расчистка территории 1-2 2 Укладка плитки на стены 2-3 3 Укладка ПВХ панелей 3-4 4 Клейка обоев 4-5 5 Замазывание щелей между плиткой 4-6 6 Крепление уголков на потолке 5-7 7 Замена розеток 7-9 8 Укладка линолеума 7-8 9 Закрепление плинтусов 9-10 10 Уборка, расстановка мебели 10-11
Cлайд 13
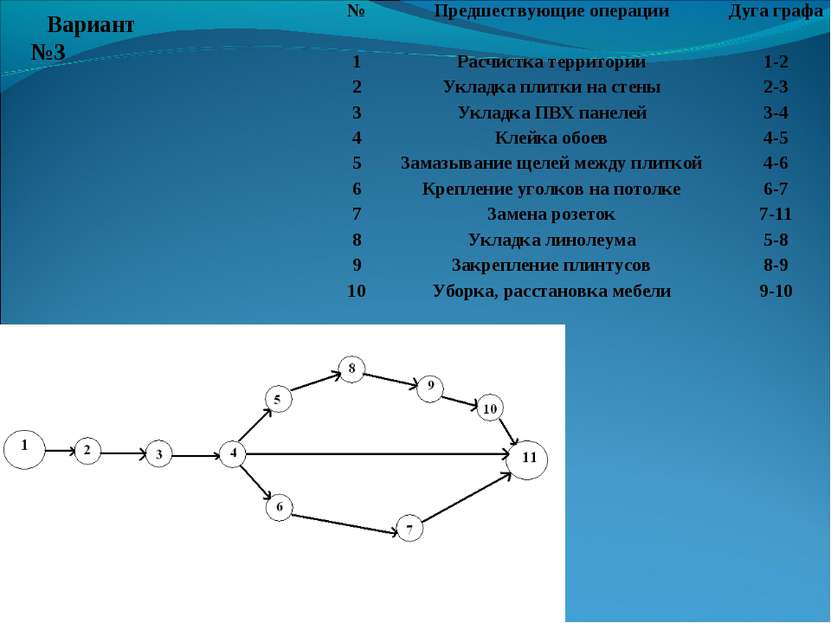
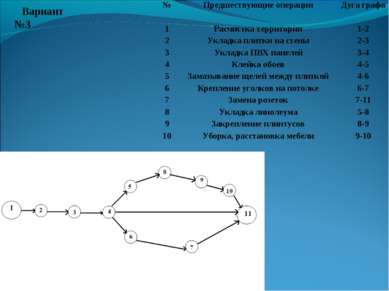Вариант №3 № Предшествующие операции Дуга графа 1 Расчистка территории 1-2 2 Укладка плитки на стены 2-3 3 Укладка ПВХ панелей 3-4 4 Клейка обоев 4-5 5 Замазывание щелей между плиткой 4-6 6 Крепление уголков на потолке 6-7 7 Замена розеток 7-11 8 Укладка линолеума 5-8 9 Закрепление плинтусов 8-9 10 Уборка, расстановка мебели 9-10
Cлайд 14
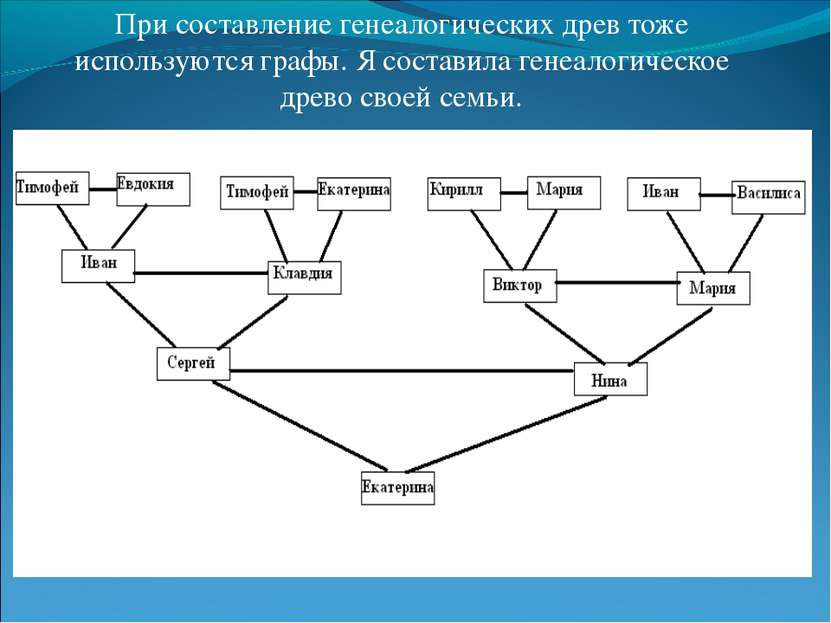
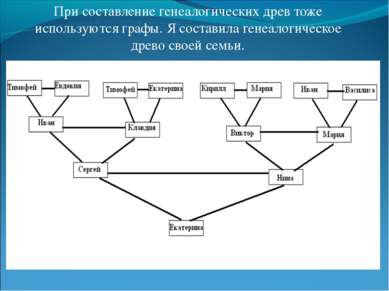При составление генеалогических древ тоже используются графы. Я составила генеалогическое древо своей семьи.
Cлайд 15
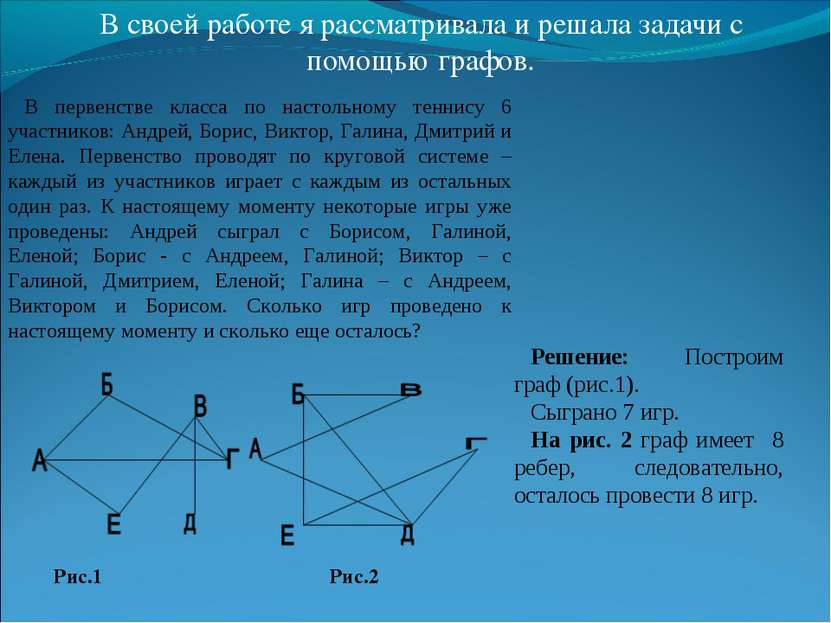
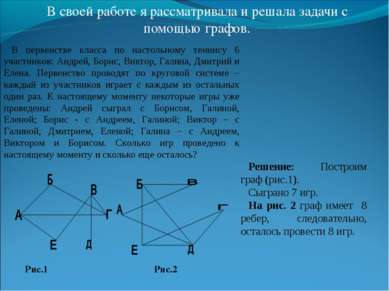В своей работе я рассматривала и решала задачи с помощью графов. В первенстве класса по настольному теннису 6 участников: Андрей, Борис, Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис - с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось? Рис.1 Рис.2 Решение: Построим граф (рис.1). Сыграно 7 игр. На рис. 2 граф имеет 8 ребер, следовательно, осталось провести 8 игр.
Cлайд 16
Пятеро друзей встретились после каникул и обменялись рукопожатиями. Каждый, здороваясь, пожал руку. Сколько всего было сделано рукопожатий? 10 рукопожатий
Cлайд 17
Из цифр 9, 7, 5, 0 составляют все возможные трехзначные числа, в которых нет одинаковых цифр. Сколько среди чисел, меньше 900?
Cлайд 18
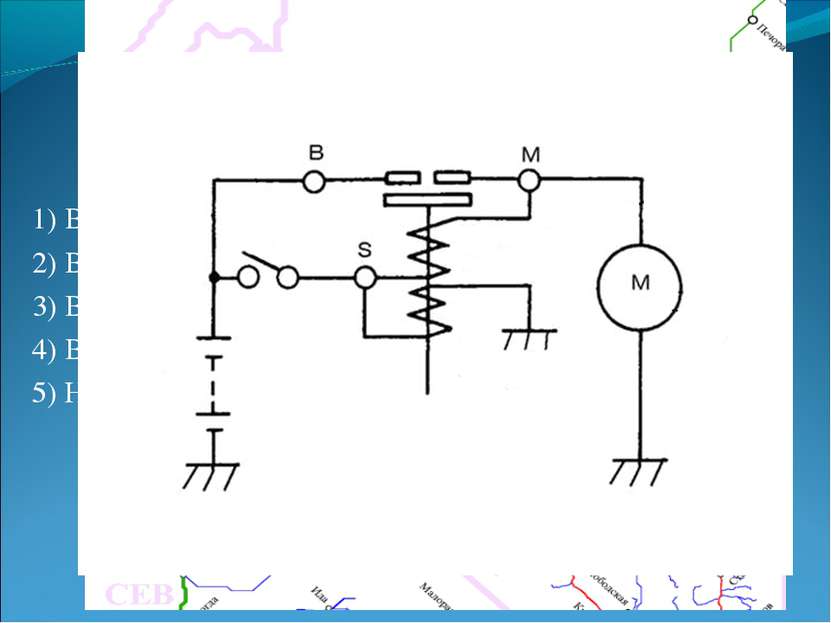
Графы представляют изучаемые факты в наглядной форме. Решение многих математических задач упрощается, если удается использовать графы. Графовые задачи позволяют развивать воображение и логическое мышление. Теория графов в настоящее время является интенсивно развивающимся разделом математики. Это объясняется тем, что в виде графовых моделей описываются многие объекты и ситуации: коммуникационные сети, схемы электрических и электронных приборов, химические молекулы, отношения между людьми и многое другое.
Cлайд 19
