X
Код презентации скопируйте его
Волшебный квадрат 9 класс
Скачать эту презентацию
Презентация на тему Волшебный квадрат 9 класс
Скачать эту презентациюCлайд 1
Презентацию на тему:«Волшебный квадрат» подготовила ученица 9 класса МОУ СОШ п.Красноозёрный, Дергачёвский район, Саратовская область Топенева Альбина Руководитель: учитель математики Топенева Загипа Захаровна Дата создания: 14.09.2011
Cлайд 2
-рассказать об истории развития магических квадратов, -рассмотреть свойства магического квадрата 4-ого порядка -уметь составлять магический квадрат 4-ого порядка -осветить актуальность магических квадратов в мире, в котором мы живём.
Cлайд 3
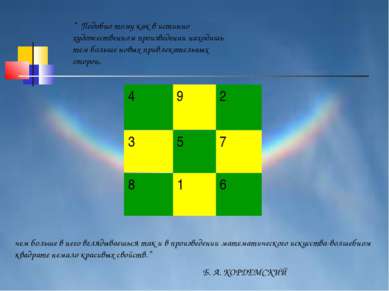” Подобно тому как в истинно художественном произведении находишь тем больше новых привлекательных сторон, чем больше в него вглядываешься так и в произведении математического искусства-волшебном квадрате немало красивых свойств.” Б. А. КОРДЕМСКИЙ 4 9 2 3 5 7 8 1 6
Cлайд 4
Магический, или волшебный квадрат — это квадратная таблица , заполненная n² числами таким образом, что сумма чисел в каждой строке, каждом столбце и на обеих диагоналях одинакова. Если в квадрате равны суммы чисел только в строках и столбцах, то он называется полумагическим. Нормальным называется магический квадрат, заполненный целыми числами от 1 до n².
Cлайд 5
Каждый элемент магического квадрата называется клеткой. Квадрат, сторона которого состоит из n клеток, содержит n² клеток и называется квадратом n-го порядка. В 16 в. Корнелий Генрих Агриппа построил квадраты 3-го, 4-го, 5-го, 6-го, 7-го, 8-го и 9-го порядков, которые были связаны с астрологией 7 планет. В 19 и 20 вв. интерес к магическим квадратам вспыхнул с новой силой. Их стали исследовать с помощью методов высшей алгебры и операционного исчисления.
Cлайд 6
Полного описания всех возможных магических квадратов не получено и до сего времени Известно, что магических квадратов 2х2 не существует. Магических квадратов 3х3 – один – остальные такие квадраты получаются из него поворотами и симметриями. Расположить натуральные числа от 1 до 9 в магический квадрат 3х3 можно 8 различными способами. Магических квадратов 4х4 уже более 800, а количество магических квадратов 5х5 близко к четверти миллиона.
Cлайд 7
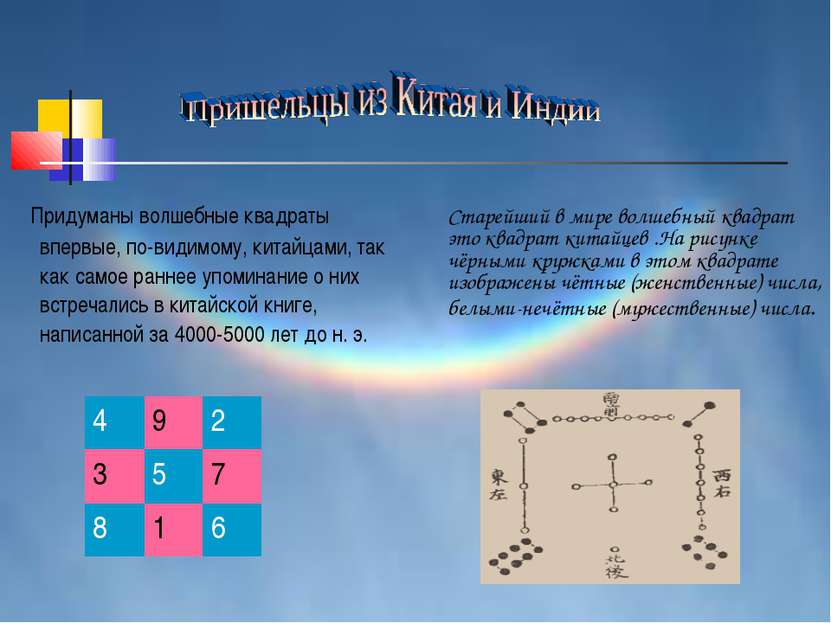
Придуманы волшебные квадраты впервые, по-видимому, китайцами, так как самое раннее упоминание о них встречались в китайской книге, написанной за 4000-5000 лет до н. э. Старейший в мире волшебный квадрат это квадрат китайцев .На рисунке чёрными кружками в этом квадрате изображены чётные (женственные) числа, белыми-нечётные (мужественные) числа. 4 9 2 3 5 7 8 1 6
Cлайд 8
Согласно легенде, во времена правления императора Ю (ок. 2200 до н.э.) из вод Хуанхэ (Желтой реки) всплыла священная черепаха, на панцире которой были начертаны таинственные иероглифы, и эти знаки известны под названием ло-шу
Cлайд 9
Латинским квадратом называется квадрат n*n клеток, в которых написаны числа от 1, до n, притом так, что в каждой строке и каждом столбце встречаются все эти числа по одному разу. Латинские квадраты 1 2 3 2 3 1 3 1 2
Cлайд 10
В 11 в. о магических квадратах узнали в Индии, а затем в Японии, где в 16 в. магическим квадратам была посвящена обширная литература. Европейцев с магическими квадратами познакомил в 15 в. византийский писатель Э.Мосхопулос. Первым квадратом, придуманным европейцем, считается квадрат А.Дюрера, изображенный на его знаменитой гравюре Меланхолия I. Любопытно, что два числа в середине нижней строки указывают год создания картины-1514.
Cлайд 11
Самый ранний уникальный магический квадрат, обнаруженный в надписи XI века в индийском городе Кхаджурахо был 4х4. И поэтому рассмотрим свойства волшебного квадрата именно такого размера, как 4х4. 7 12 1 14 2 13 8 11 16 3 10 5 9 6 15 4
Cлайд 12
Сумма чисел, расположенных по углам нашего волшебного квадрата, равна 34, т. е. тому же числу, что и сумма чисел вдоль каждого ряда квадрата Суммы чисел в каждом из маленьких квадратов (в 4 клетки), примыкающих к вершинам данного квадрата, и в таком же центральном квадрате тоже одинаковы и каждая из них равна 34: 1+14+12+7=34 11+13+2+8=34 10+5+3+16=34 15+4+6+9=34 7+6+11+10=34 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16
Cлайд 13
В каждой строке есть пара рядом стоящих чисел, сумма которых 15, и ещё пара тоже рядом стоящих чисел, сумма которых 19. Подсчитаем теперь сумму квадратов чисел отдельно в двух крайних строках и двух средних: Как видите получились попарно равные суммы! 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16
Cлайд 14
Суммы квадратов чисел двух крайних столбцов равны между собой и суммы квадратов чисел двух средних столбцов тоже одинаковы Если в данный квадрат вписать ещё один квадрат с вершинами в серединах сторон данного квадрата, то следует ожидать следующее: 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16
Cлайд 15
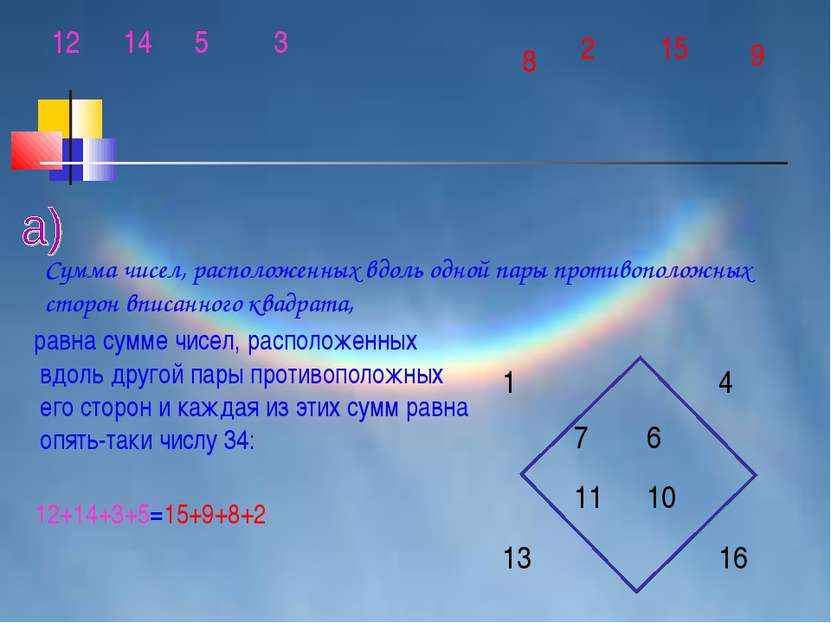
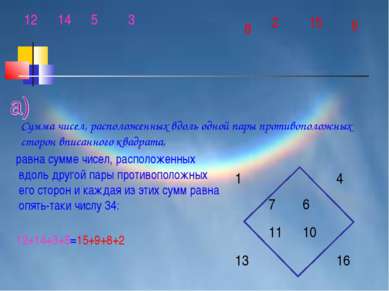равна сумме чисел, расположенных вдоль другой пары противоположных его сторон и каждая из этих сумм равна опять-таки числу 34: 12+14+3+5=15+9+8+2 Сумма чисел, расположенных вдоль одной пары противоположных сторон вписанного квадрата, 1 4 7 6 11 10 13 16 14 2 8 9 12 5 3 15
Cлайд 16
Ещё интереснее то, что равны между собой даже суммы квадратов и суммы кубов этих чисел: При обмене местами отдельных строк или столбцов волшебного квадрата некоторые из вышеперечисленных его свойств могут исчезнуть, но могут и все сохраниться и даже появиться новые. Например, поменяем местами 1 и 2 строку данного квадрата. 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16 12 7 6 9 1 14 15 4 8 11 10 5 13 2 3 16 1 14 15 4 12 7 6 9 8 11 10 5 13 2 3 16
Cлайд 17
Суммы чисел вдоль строк и столбцов, конечно, не изменились, но суммы чисел по диагоналям стали иными, не равными 34. волшебный квадрат потерял часть своих основных свойств, стал «неполным волшебным квадратом». 12 1 8 13 7 14 11 2 6 15 10 3 9 4 5 16 Продолжая обменивать местами строки и столбцы квадрата, мы будем получать всё новые и новые волшебные квадраты из 16 чисел. Некоторые из них будут обладать основными свойствами. 12 7 6 9 1 14 15 4 8 11 10 5 13 2 3 16
Cлайд 18
Расположить в шестнадцати клетках все целые числа от 1 до 16 по порядку а б в г 1 2 3 4 Как самому составить волшебный квадрат? Порядок следования чисел в строках «в» и «г» изменить на обратный и обменять местами строки «б» и «в»: а б в г 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 2 3 4 12 11 10 9 5 6 7 8 16 15 14 13
Cлайд 19
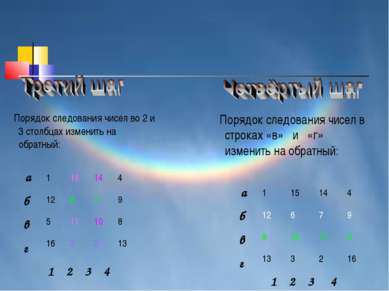Порядок следования чисел во 2 и 3 столбцах изменить на обратный: 1 2 3 4 а б в г Порядок следования чисел в строках «в» и «г» изменить на обратный: а б в г 1 2 3 4 1 15 14 4 12 6 7 9 5 11 10 8 16 2 3 13 1 15 14 4 12 6 7 9 8 10 11 5 13 3 2 16
Cлайд 20
Волшебный квадрат готов! Можете проверить. Каждая из интересующих нас сумм равна 34 ( это число называется константой волшебного квадрата).
Cлайд 21
Актуальность ВОЛШЕБНЫХ квадратов в мире, в котором мы живем -Насколько интересны ВОЛШЕБНЫЕ квадраты в мире, в котором мы живем? -Я провела небольшое исследование.
Cлайд 22
Для этого сделала опрос среди учащихся 2 – 6 классов. Участие приняли 60 человек. Результат представляю в виде круговой диаграммы. ВЫВОД: магические квадраты в среде детей популярны... 66% 16% 18%
Cлайд 23
Для родителей учеников приготовила экспресс-анкету 1)ваш ребенок увлекается магическими квадратами а)да, б)нет),в)иногда, 2)часто оказываете помощь при выполнении домашнего задания а)да, б)нет),в)иногда, 3)успеваемость вашего ребенка а)отличная, б) хорошая, в)удовлетворительная.
Cлайд 24
Выясняю интересный факт: при решении задач меньше обращаются за помощью те, кто увлечен магическими квадратами. У этих же ребят и успеваемость лучше по сравнению с теми, кто к квадратам волшебным равнодушен. Делаю собственный вывод: В начальных и средних классах очень интересно ребятам решать и составлять магические квадраты. Это помогает в дальнейшем хорошо решать задачи и разбираться в математических упражнениях.
Cлайд 25
А что ответило взрослое население моего поселка? Действительно, сейчас идет волна нового увлечения игрой СУДОКУ. В основном потому, что по своей сути - это интереснейшая головоломка. Постараюсь рассказать о судоку. Судоку — это головоломка-пазл с числами, ставшая в последнее время очень популярной. В переводе с японского "су" — "цифра", "доку" — "стоящая отдельно". Иногда судоку называют «магическим квадратом». Игровое поле представляет собой квадрат размером 9x9, разделённый на меньшие квадраты со стороной в 3 клетки. Таким образом, всё игровое поле состоит из 81 клетки. В некоторых из них уже в начале игры стоят числа (от 1 до 9). В зависимости от того, сколько клеток уже заполнены, конкретную судоку можно отнести к лёгким или сложным.
Cлайд 26
Продолжим дальше. В чём ещё актуальность волшебных квадратов в современном мире? Обратимся к Интернету. Выясняем, что существует нумерологический анализатор «Пифагор». В чем его суть? Это мощная система анализа магического квадрата Пифагора и нумерологической карты, позволяющая проанализировать и понять характер, поведение и мотивацию не только себя, любимого, но и других людей. При помощи анализатора "Пифагор" можно хорошо подготовиться к предстоящей встрече еще до визуального контакта с человеком. Например, после знакомства в сети Интернет, собеседования по телефону и так далее.
Cлайд 27
В современном мире с помощью нумерологической программы "Пифагор" преподаватели смогут быстрее понять склонности ученика к тому или иному предмету, лучше преподнести материал во время индивидуальных занятий. Психоаналитики смогут быстрее найти проблемные вопросы клиентов. Персоналу отдела кадров программа поможет быстрее разобрать полученные резюме и выделить самых перспективных претендентов.
Cлайд 28
Продолжая поиски опять-таки в интернете, поражаемся размаху использования магических квадратов. Теперь же они - элементы прогресса нанотехнологии. Недавно в Интернете появилась интересная информация : фирма "Тошиба" , разрабатывая качественные телевизионные экраны, пришла к выводу, что цветовые ячейки выгодно компоновать по принципу магических квадратов. В этом случае резко повышаются как четкость изображений , так и цветовые переходы. Идеальные магические квадраты имеют в два раза больше цепей ячеек, дающих магическую сумму. Следовательно, и качество изображений экрана телевизора должно еще более улучшиться.
Cлайд 29
В своей презентации я рассмотрела вопросы, связанные с магическими квадратами. Мне нравилось и нравится составлять волшебные квадраты и думаю, что буду и в дальнейшем совершенствовать свои знания в этом направлении. 4 9 2 3 5 7 8 1 6
Cлайд 30
Литература 1) Кордемский Б.А. Математическая смекалка. — ГИФМЛ, 1958. — 576 с. 2) Савин А. П., Я познаю мир.- АСТ, 2004.-475,(5) с. 3)http://www.stereo.ru/whatishat/php?artikle id=254 4) http://narod/ru/disk/2927154000/Магия _чисел_и_слов%20
Cлайд 31
