X
Код презентации скопируйте его
Устное решение квадратного уравнения
Скачать эту презентациюПрезентация на тему Устное решение квадратного уравнения
Скачать эту презентациюCлайд 1
 Приёмы устного решения квадратного уравнения Муниципальное общеобразовательное учреждение «Гимназия №53» Бойко Т.А. учитель математики
Приёмы устного решения квадратного уравнения Муниципальное общеобразовательное учреждение «Гимназия №53» Бойко Т.А. учитель математики
Cлайд 4
 Извлечения квадратного корня Из натурального числа 92 *16 =96 81 1116 1116 3*24 = 18 1 224 224 186 6 28 8 устно
Извлечения квадратного корня Из натурального числа 92 *16 =96 81 1116 1116 3*24 = 18 1 224 224 186 6 28 8 устно
Cлайд 5
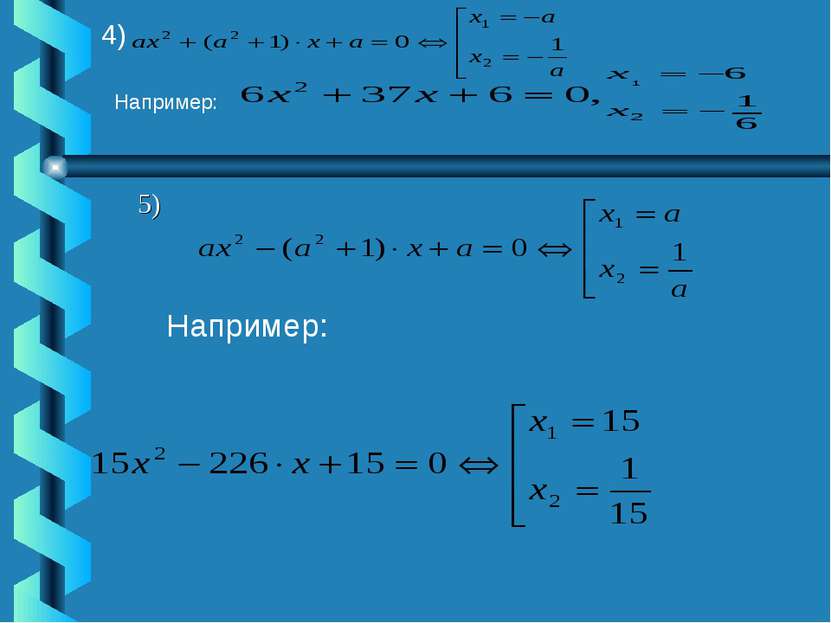
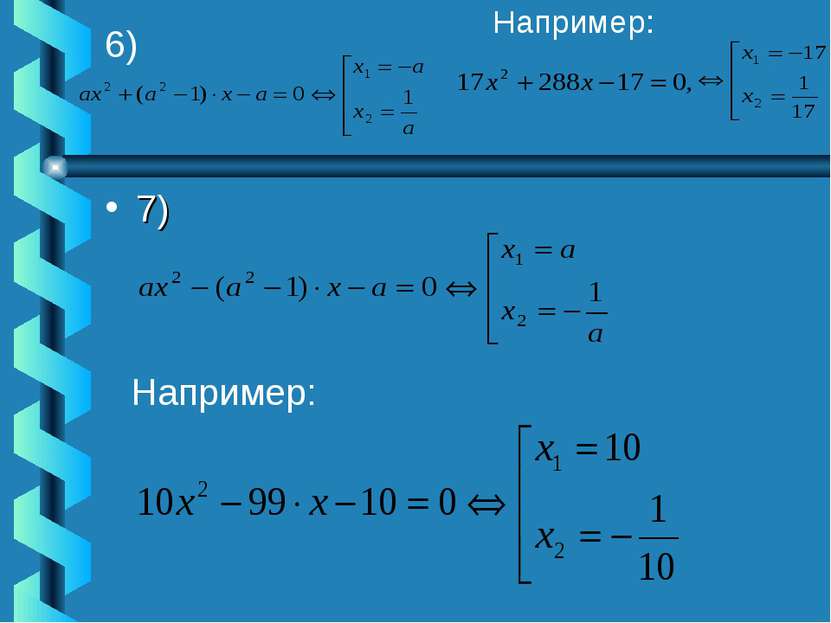
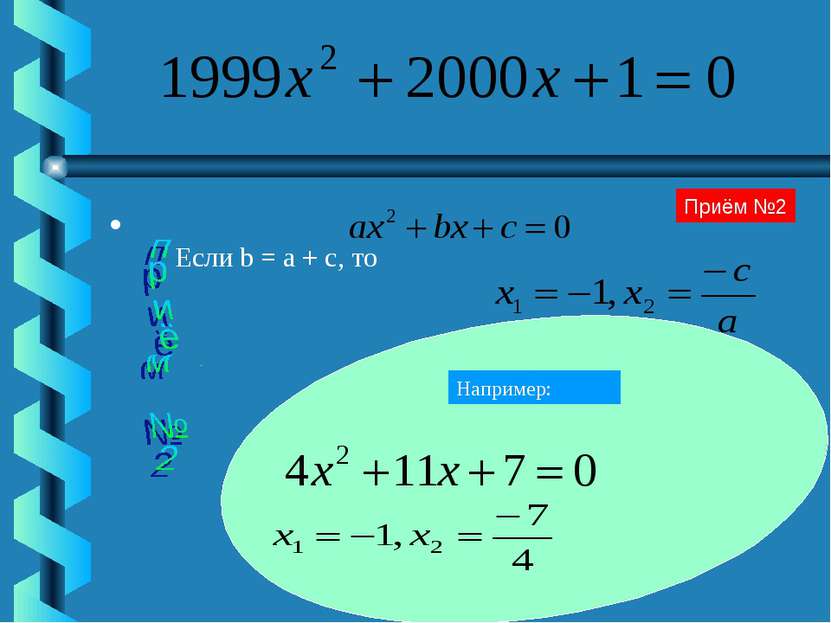
 Приём «Коэффициентов»: 1) Если а+в+с=0, то 2) Если в = а + с, то 3) Если Используя приёмы 1) -3) можно придумывать уравнения с рациональными корнями. , то приём «Переброски»
Приём «Коэффициентов»: 1) Если а+в+с=0, то 2) Если в = а + с, то 3) Если Используя приёмы 1) -3) можно придумывать уравнения с рациональными корнями. , то приём «Переброски»
Cлайд 10
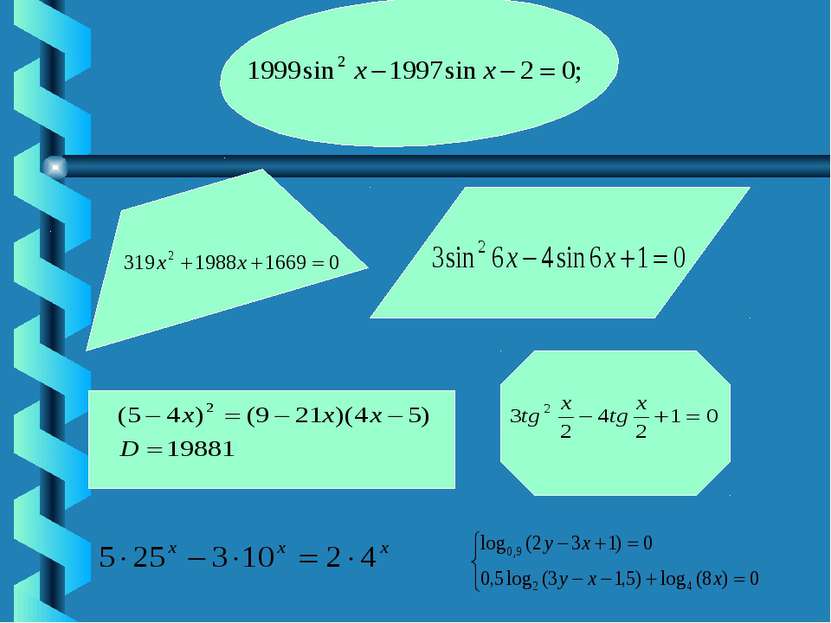
 Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных , иррациональных уравнений и неравенств. В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных , иррациональных уравнений и неравенств. В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие приёмы решения квадратных уравнений, которые позволяют очень быстро и рационально решать квадратные уравнения.
Cлайд 11
 Приёмы устного решения квадратного уравнения 1) 2 ) приём «коэффициентов» 3) приём «переброски»
Приёмы устного решения квадратного уравнения 1) 2 ) приём «коэффициентов» 3) приём «переброски»
Cлайд 12
 Обобщить и систематизировать изученный материал по теме: «Квадратные уравнения». Научить учащихся приёмам устного решения квадратных уравнений. Развивать внимание и логическое мышление. Воспитывать культуру поведения .
Обобщить и систематизировать изученный материал по теме: «Квадратные уравнения». Научить учащихся приёмам устного решения квадратных уравнений. Развивать внимание и логическое мышление. Воспитывать культуру поведения .
Cлайд 13
 1 корень: x = 0 2корня, если: а и с имеют разные знаки Нет корней, если: а и с имеют одинаковые знаки 2корня b=o c=0 b=0 c≠0 b≠0 c=0
1 корень: x = 0 2корня, если: а и с имеют разные знаки Нет корней, если: а и с имеют одинаковые знаки 2корня b=o c=0 b=0 c≠0 b≠0 c=0
Cлайд 18
 Пусть дано квадратное уравнение где 1.Если a + b + c=0 (т.е сумма коэффициентов равна нулю), то Доказательство. Разделим обе части уравнения на получим приведённое квадратное уравнение По теореме Виета По условию a + b +c =0, откуда b= - a – c. Значит, Получаем что и требовалось доказать.
Пусть дано квадратное уравнение где 1.Если a + b + c=0 (т.е сумма коэффициентов равна нулю), то Доказательство. Разделим обе части уравнения на получим приведённое квадратное уравнение По теореме Виета По условию a + b +c =0, откуда b= - a – c. Значит, Получаем что и требовалось доказать.
Cлайд 25
 Используя приёмы решения 1) – 3),вы можете придумывать уравнения с рациональными корнями. Например, возьмём уравнение (Корни 2 и 3), 6 делится на 1,2,3,6 6=1*6 6=6*1 6=2*3 6=3*2 Отсюда уравнения: ________________ 1) 2) 3) 4) 5) 6) 7) Одно уравнение дало ещё 7 уравнений с рациональными корнями. -------------------------------------------------
Используя приёмы решения 1) – 3),вы можете придумывать уравнения с рациональными корнями. Например, возьмём уравнение (Корни 2 и 3), 6 делится на 1,2,3,6 6=1*6 6=6*1 6=2*3 6=3*2 Отсюда уравнения: ________________ 1) 2) 3) 4) 5) 6) 7) Одно уравнение дало ещё 7 уравнений с рациональными корнями. -------------------------------------------------
Cлайд 26
 По праву достойна в стихах быть воспета свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни – и дробь уж готова? В числителе с , в знаменателе а. А сумма корней тоже дроби равна. Хоть с минусом дробь, что за беда. В числителе в, в знаменателе а.
По праву достойна в стихах быть воспета свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни – и дробь уж готова? В числителе с , в знаменателе а. А сумма корней тоже дроби равна. Хоть с минусом дробь, что за беда. В числителе в, в знаменателе а.
Cлайд 27
 Найти №№ 505 – 573 -------------------------------- квадратные уравнения, которые можно решить устно, используя изученные приёмы.
Найти №№ 505 – 573 -------------------------------- квадратные уравнения, которые можно решить устно, используя изученные приёмы.
Cлайд 28
 Выводы: данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики; овладение данными приёмами поможет учащимся экономить время и эффективно решать уравнения; потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов; владение алгоритмом извлечения квадратного корня из натурального числа.
Выводы: данные приёмы решения заслуживают внимания, поскольку они не отражены в школьных учебниках математики; овладение данными приёмами поможет учащимся экономить время и эффективно решать уравнения; потребность в быстром решении обусловлена применением тестовой системы вступительных экзаменов; владение алгоритмом извлечения квадратного корня из натурального числа.