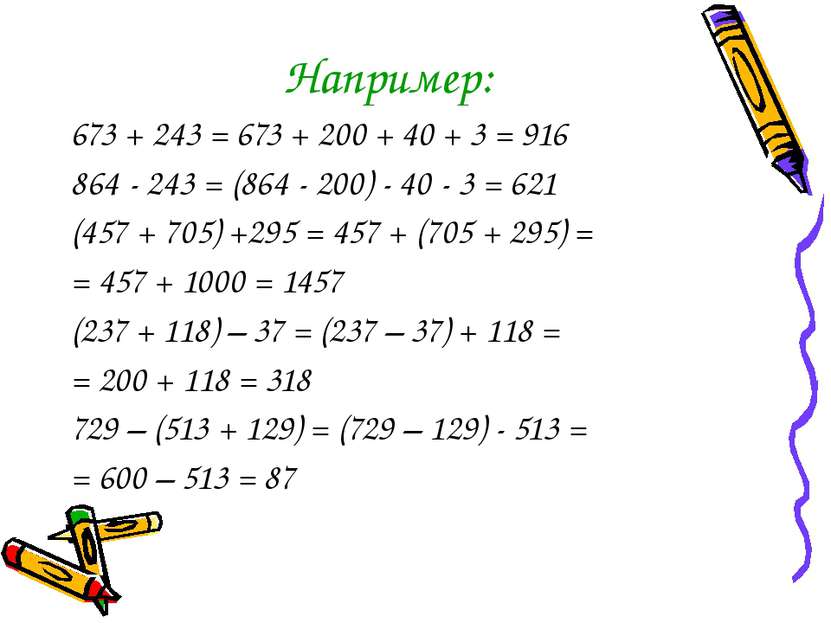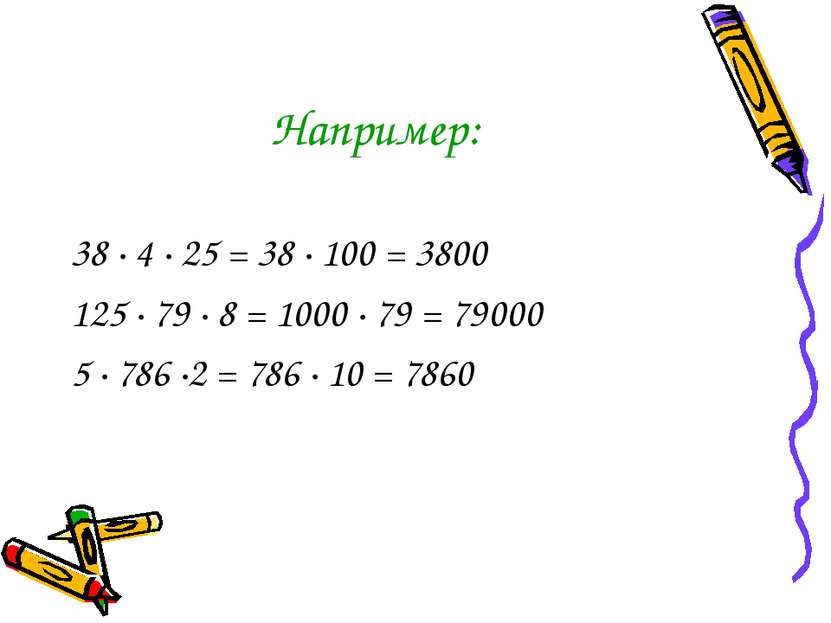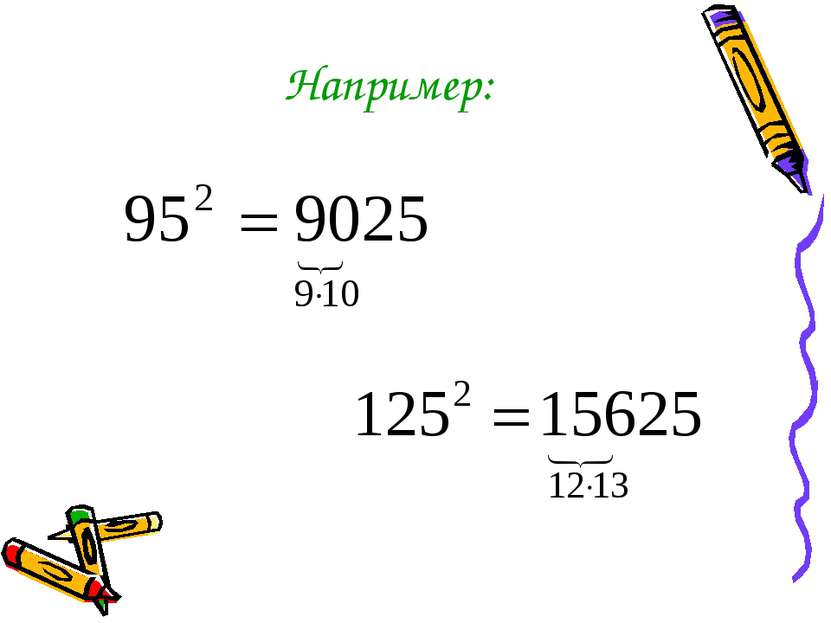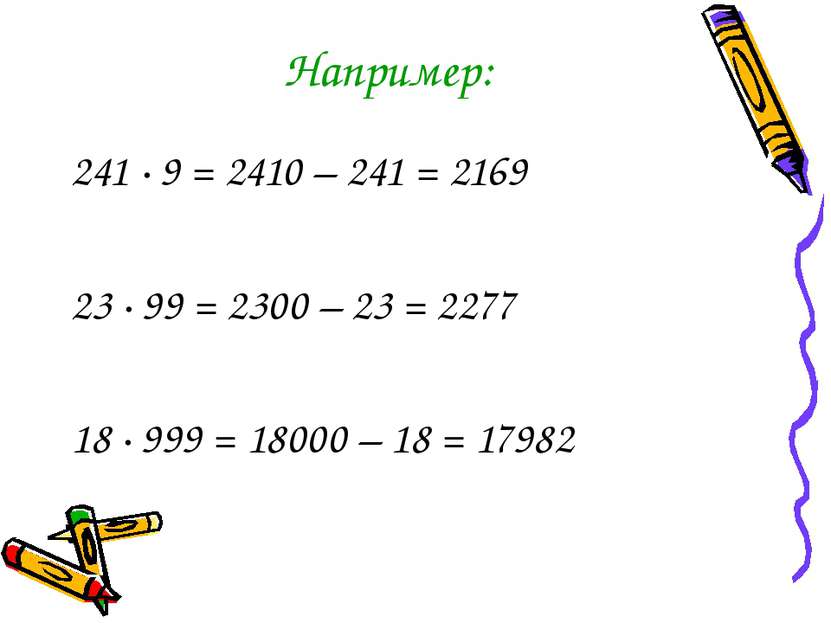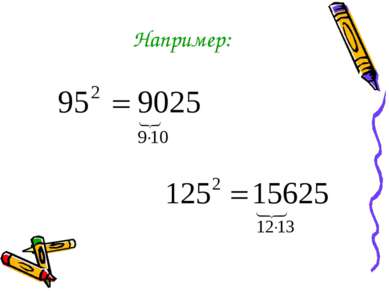X
Код презентации скопируйте его
Быстрый счет без калькулятора
Скачать эту презентацию
Презентация на тему Быстрый счет без калькулятора
Скачать эту презентациюCлайд 1
Выполнили обучающиеся 5 «А» класса МОУ «Обоянская средняя общеобразовательная школа №2» Учитель Марова С.Н.
Cлайд 2
Умеете ли Вы считать? Каждый, конечно скажет: «Да!» Это очень важные умения, так как вычислительные навыки являются фундаментом изучения математики и других учебных дисциплин. Но сегодня особо ценится умение не только правильно, но и быстро считать.
Cлайд 3
Хорошо ли Вы считаете? Об умении считать можно судить: - по умению производить устные и письменные вычисления, - по рациональной организации хода вычисления, - по умению убеждаться в правильности полученных результатов. Качество вычислительных умений определяется двумя вещами: знанием правил; знанием алгоритмов вычислений.
Cлайд 4
Проблема исследования Много ошибок при выполнении вычислений, сложности при устном счёте.
Cлайд 5
Основополагающий вопрос Как за короткое время научиться быстро считать, если ты обыкновенный школьник, а не вундеркинд?
Cлайд 6
Гипотеза Существуют специальные способы выполнения действий, которые позволяют свести вычисления к устным, рассчитанные на ум «обычного» человека и не требующие уникальных способностей. Главное – небольшая тренировка.
Cлайд 7
Цель проекта Найти и освоить приёмы, позволяющие выполнить действия с числами быстро (устно) и безошибочно. Создать буклет, в котором разместить информацию о наиболее полезных для школьников приёмах быстрого счёта.
Cлайд 8
Творческое название исследовательского проекта БЫСТРЫЙ СЧЁТ БЕЗ КАЛЬКУЛЯТОРА
Cлайд 9
1) Общие приемы устного счета. 2) Специальные приемы устного счета: а) прием округления; б) умножение и деление на 4,8,…; в) умножение и деление на 5, 25; г) умножение на 1,5; д) прием возведения в квадрат числа оканчивающегося на 5; е) умножение на 9, 99, 999,…; ж) умножение на 11, 101, 1001. Содержание работы
Cлайд 10
Общие приемы устного счета разложение каждого слагаемого на разряды; использование переместительного и сочетательного свойства сложения (умножения); использование свойств вычитания; использование распределительного свойства при умножении и делении.
Cлайд 11
Например: 673 + 243 = 673 + 200 + 40 + 3 = 916 864 - 243 = (864 - 200) - 40 - 3 = 621 (457 + 705) +295 = 457 + (705 + 295) = = 457 + 1000 = 1457 (237 + 118) – 37 = (237 – 37) + 118 = = 200 + 118 = 318 729 – (513 + 129) = (729 – 129) - 513 = = 600 – 513 = 87
Cлайд 12
Запомни! 5 · 2 = 10 25 · 4 = 100 125 · 8 = 1000 125 · 16=125· 8· 2=2000
Cлайд 13
Например: 38 · 4 · 25 = 38 · 100 = 3800 125 · 79 · 8 = 1000 · 79 = 79000 5 · 786 ·2 = 786 · 10 = 7860
Cлайд 14
Распределительное свойство при умножении и делении (а + b)· с = а · с + b · с (а – b)· с = а · с – b · с
Cлайд 15
Например: 198 · 4=(200–2) ·4=200 ·4 – 2·4=800 – 8=792 91 · 8 = (90 + 1) · 8=90 ·8 + 1 · 8=720 + 8=728 69 · 27 + 31 · 27=(69 +31) · 27=100 · 27=2700 438 ·90–238·90=(438–238)·90=200 ·90=1800 (80 + 240) : 8 = 80 : 8 + 240 : 8 =10 + 30= 40 405 :27+135 :27=(405+135) : 27=540 :27=20
Cлайд 16
Прием округления 1. Если одно из слагаемых увеличить на несколько единиц, то из полученной суммы надо вычесть столько же единиц. или 2. Если одно из слагаемых увеличить на несколько единиц, а второе уменьшить на столько же единиц, то сумма не изменится. 364+592=364+(592+8) –8= 364+600 – 8 =956 997+856=(997+3)+(856 – 3)=1000+853=1853
Cлайд 17
3. Если вычитаемое увеличить на несколько единиц и уменьшаемое увеличить на столько же единиц, то разность не изменится. 4. Если один из множителей уменьшить в несколько раз, а другой увеличить в такое же число раз, то произведение не изменится. 5. Если делимое уменьшить в несколько раз, то частное уменьшиться в несколько раз, поэтому, чтобы результат не изменился, то его надо увеличивать во столько же раз. Прием округления 1351 – 994 = (1351+6) – (994+6)=1357 – 1000=357 50 · 24=(50 · 2)· (24 : 2)=100 · 12=1200 720:6=((720:2):6·2)=(360:6)·2=60·2=120
Cлайд 18
Умножение и деление на 4, 8, 16,… Чтобы число умножить на 4, его дважды удваивают. 213· 4=(213·2)·2=426· 2=852 Чтобы число разделить на 4, его дважды делят на 2. 124:4=(124:2):2=62:2=31 Чтобы умножить число на 8 его трижды удваивают. Чтобы умножить число на 16 его четырежды удваивают и т.д. При делении числа на 8 необходимо его трижды поделить на 2; При делении числа на 16 необходимо его четыре раза поделить на 2.
Cлайд 19
Умножение и деление на 5, 25, 125 Чтобы число умножить на 5, нужно умножить его на 10 и разделить на 2. Чтобы разделить число на 5, нужно умножить его на 2 и разделить на 10. Чтобы число умножить на 25, нужно умножить его на 100 (т.е. приписать два нуля) и разделить на 4. При умножении числа на 125 необходимо умножить его на 1000 (т.е. приписать к нему три нуля) и разделить его на 8.
Cлайд 20
Например: 138 · 5 = (138 · 10) : 2 = 1380 : 2 = 690 71 : 5 = 71 · 2 : 10= 142 : 10 = 14,2 348 · 25 = 34800 : 4 = 8700 72 · 125=72 · 1000 : 8=72000 : 8=9000
Cлайд 21
Умножение на 1,5 Чтобы умножить число на 1,5, нужно к исходному числу прибавить его половину. 24 · 1,5 = 24 + 12 = 36 129 · 1,5 = 129 + 64,5 = 193,5
Cлайд 22
Возведение в квадрат числа, оканчивающегося цифрой 5 Чтобы возвести в квадрат число, оканчивающееся цифрой 5 (например, 65), умножают число его десятков (6) на число десятков, увеличенное на 1 (на6+1 = 7), и к полученному числу приписывают 25 Ответ: 4225
Cлайд 23
Например:
Cлайд 24
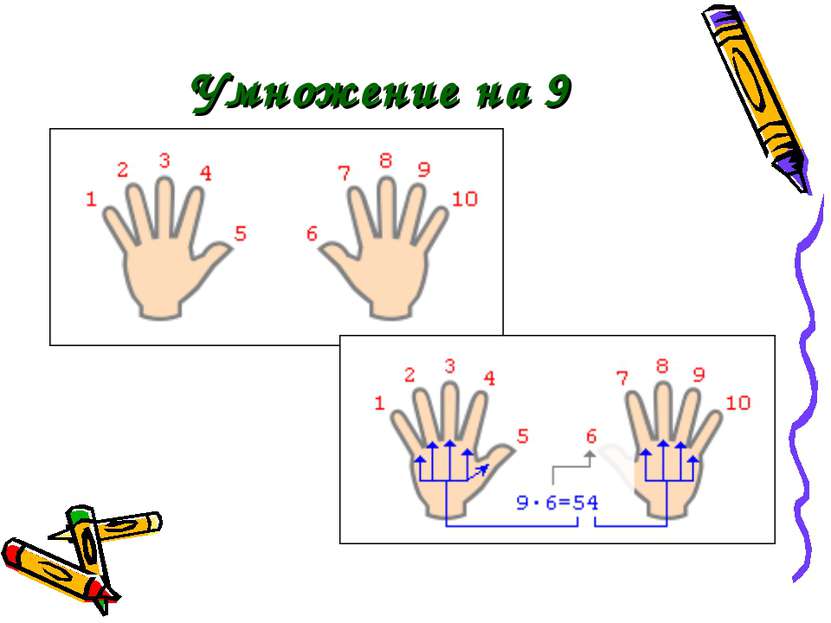
Умножение на 9, 99, 999,… Чтобы умножить число на 9, к нему приписывают 0 и отнимают исходное число. Чтобы умножить число на 99 надо приписать к нему два нуля и вычесть исходное число. Чтобы умножить число на 999 надо приписать к нему три нуля и вычесть исходное число
Cлайд 25
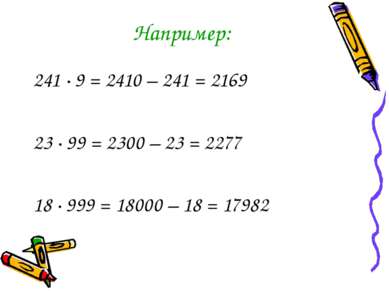Например: 241 · 9 = 2410 – 241 = 2169 23 ∙ 99 = 2300 – 23 = 2277 18 ∙ 999 = 18000 – 18 = 17982
Cлайд 26
Умножение на 9
Cлайд 27
Умножение на 11 Чтобы умножить число на 11, к нему приписывают 0 и прибавляют исходное число. 72 · 11 = 720 + 72 = 792 2. Чтобы умножить двузначное число, сумма цифр которого не превышает 10, на 11, надо цифры этого числа раздвинуть и поставить между ними сумму этих цифр 72 ∙ 11 = 7(7+2)2 = 792
Cлайд 28
Умножение на 11 Чтобы умножить на 11 двузначное число, сумма цифр которого ≥ 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить 1, а вторую и последнюю оставить без изменений. 94 ∙ 11=9(9+4)4=9(13)4 =(9+1)34=1034
Cлайд 29
Умножение на 101, 1001 Чтобы умножить число на 101, нужно приписать к нему два нуля и прибавить исходное число. Чтобы умножить число на 1001, нужно приписать к нему три нуля и прибавить исходное число. 145 · 101 = 14500 + 145 = 14645 27 · 101 = 2700 + 27 = 2727 53 · 1001 = 53000 + 53 = 53053 461 · 1001=461000 +461=461461
Cлайд 30
Заключение Действительно, существуют специальные способы выполнения действий, которые позволяют свести вычисления к устным, быстрым, не требующие уникальных способностей, рассчитанные на ум «обычного» человека. Главное – небольшая тренировка.
Cлайд 31
Благодарим за внимание!
