X
Код презентации скопируйте его
Понятие движения (9 класс)
Скачать эту презентациюПрезентация на тему Понятие движения (9 класс)
Скачать эту презентациюCлайд 2
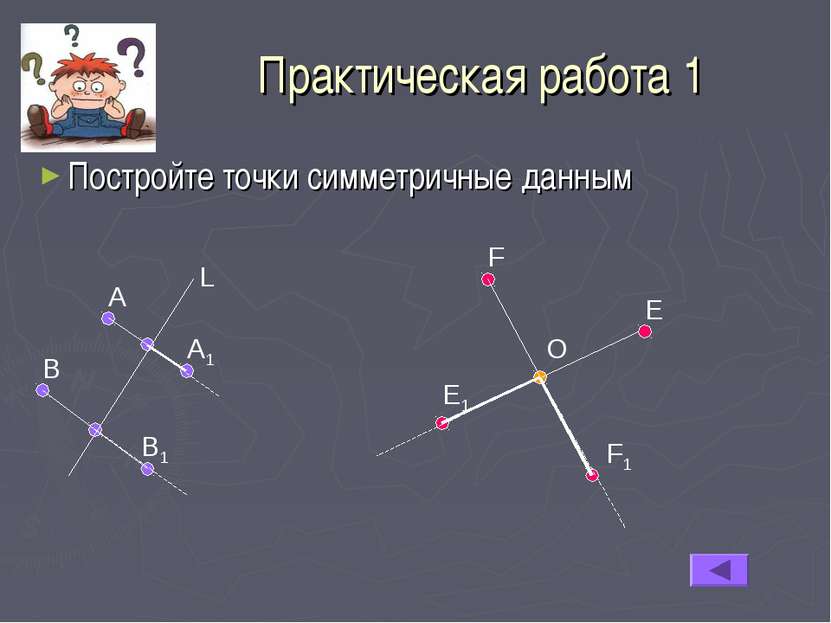
 План урока Осевая симметрия Центральная симметрия Практическая работа Понятие отображения плоскости на себя Понятие движения Решение задач Итоги урока
План урока Осевая симметрия Центральная симметрия Практическая работа Понятие отображения плоскости на себя Понятие движения Решение задач Итоги урока
Cлайд 3
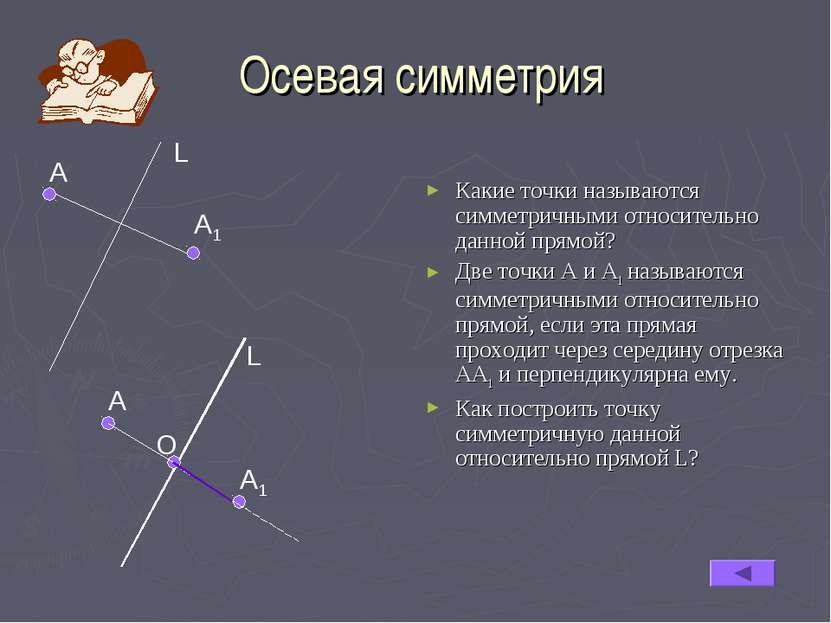
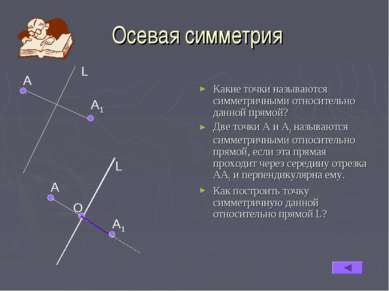 Осевая симметрия Какие точки называются симметричными относительно данной прямой? Две точки А и А1 называются симметричными относительно прямой, если эта прямая проходит через середину отрезка АА1 и перпендикулярна ему. Как построить точку симметричную данной относительно прямой L? А L А1 А О А1 L
Осевая симметрия Какие точки называются симметричными относительно данной прямой? Две точки А и А1 называются симметричными относительно прямой, если эта прямая проходит через середину отрезка АА1 и перпендикулярна ему. Как построить точку симметричную данной относительно прямой L? А L А1 А О А1 L
Cлайд 4
 Центральная симметрия Какие точки называются симметричными относительно данной точки? Две точки А и А1 называются симметричными относительно точки, если эта точка является серединой отрезка АА1. Как построить точку симметричную данной относительно некоторой точки О? А О А1 А О А1
Центральная симметрия Какие точки называются симметричными относительно данной точки? Две точки А и А1 называются симметричными относительно точки, если эта точка является серединой отрезка АА1. Как построить точку симметричную данной относительно некоторой точки О? А О А1 А О А1
Cлайд 6
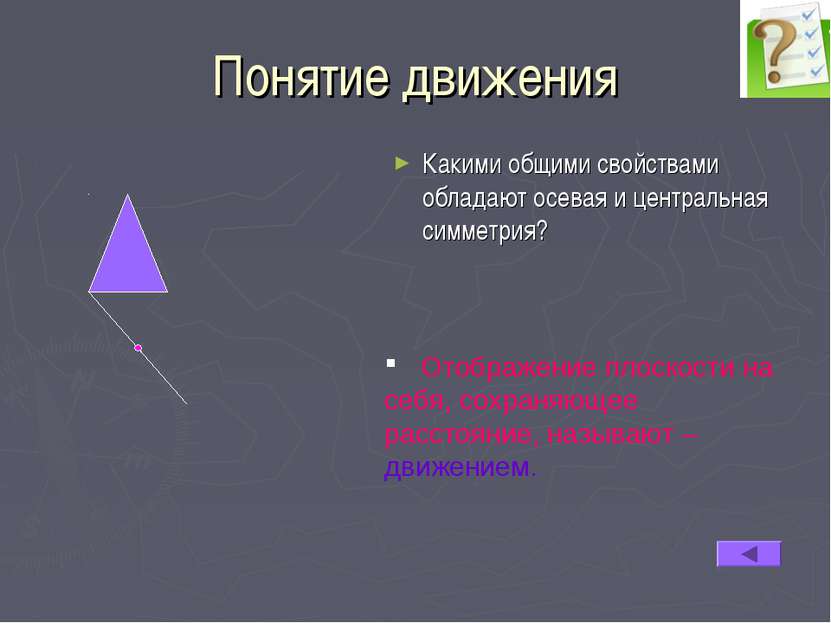
 Отображение плоскости на себя Пусть каждой точке плоскости ставится в соответствие какая –то точка этой плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. В таком случае говорят, что дано отображение плоскости на себя.
Отображение плоскости на себя Пусть каждой точке плоскости ставится в соответствие какая –то точка этой плоскости, причем любая точка плоскости оказывается сопоставленной некоторой точке. В таком случае говорят, что дано отображение плоскости на себя.