X
Код презентации скопируйте его
Расстояния между прямыми
Скачать эту презентацию
![; ; ; , ; ; , ; ] а) ((АР); (ВС)) = 900 б) ((АР); (СQ)) = KMС = arccos в) ((А...](https://bigslide.ru/images/39/38094/831/img8.jpg "; ; ; , ; ; , ; ] а) ((АР); (ВС)) = 900 б) ((АР); (СQ)) = KMС = arccos в) ((А...")
Презентация на тему Расстояния между прямыми
Скачать эту презентациюCлайд 1
Урок 11 Расстояния между прямыми
Cлайд 2
Определение. Углом между прямыми называется меньший из двух углов между лучами, которые этим прямым соответственно параллельны. Следствия. Если а || b, то (a; b) = 0 ; Если а b = O, то (a; b) – тот из образовавшихся углов с вершиной О, который не тупой. 3) Если а b, то (a; b) = (a’; b’), где a’ || a; b’ || b; a’ b’ = O’. Таким образом, 0 (a; b) 90 .
Cлайд 3
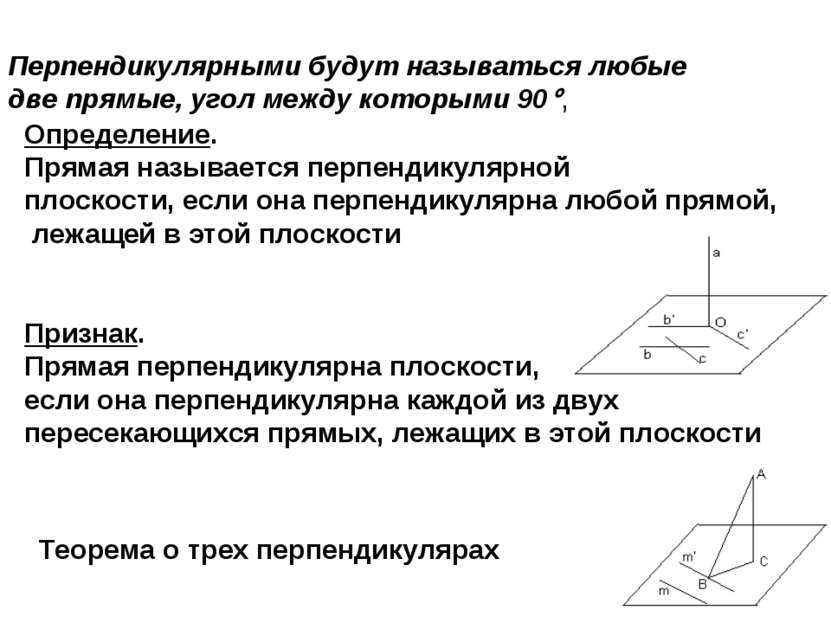
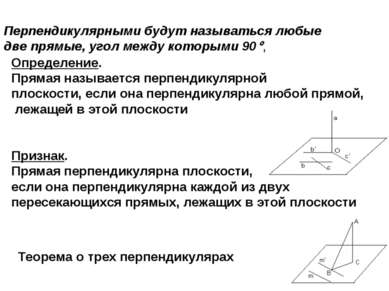Перпендикулярными будут называться любые две прямые, угол между которыми 90 , Определение. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости Признак. Прямая перпендикулярна плоскости, если она перпендикулярна каждой из двух пересекающихся прямых, лежащих в этой плоскости Теорема о трех перпендикулярах
Cлайд 4
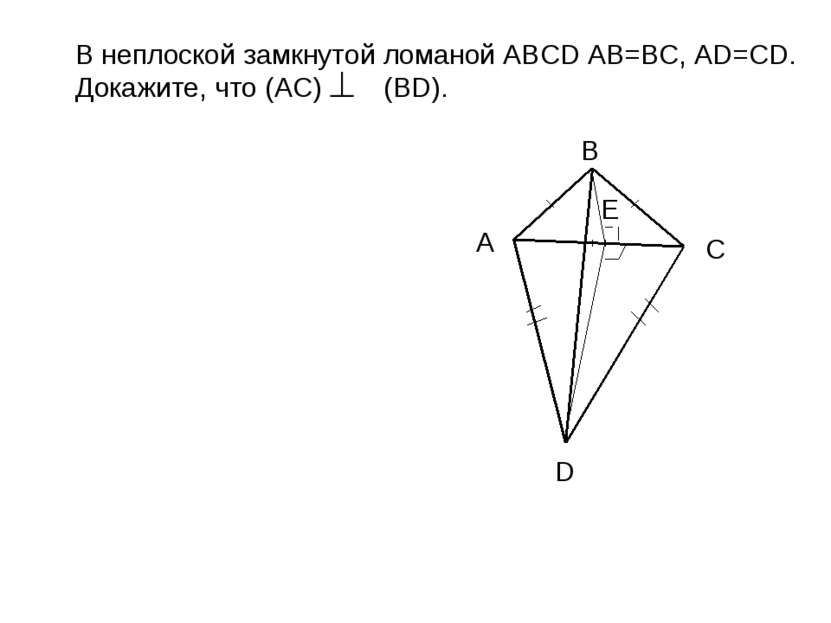
Верно ли, что прямая, перпендикулярная двум сторонам треугольника, перпендикулярна его третьей стороне?
Cлайд 5
В неплоской замкнутой ломаной ABCD AB=BC, AD=CD. Докажите, что (АС) (BD). В А Е С D
Cлайд 6
Точка А не лежит на прямой а. Какую фигуру образуют все прямые, проходящие через точку А и перпендикулярные прямой а?
Cлайд 7
Проверьте равносильность утверждений: Две прямые перпендикулярны Через каждую из них проходит плоскость, перпендикулярная другой прямой 2) | a и b b a. b a а) б)
Cлайд 8
2. Пусть РАВС – правильный тетраэдр, точка Q – центр его основания, точка К – середина ребра РВ, точка L – середина ребра АС. Вычислите угол между прямыми: А) АР и ВС; б)АР и СQ; в) АР и СЛ; г) АК и ВС; д) АК и РL; е) АQ и KL.
Cлайд 9
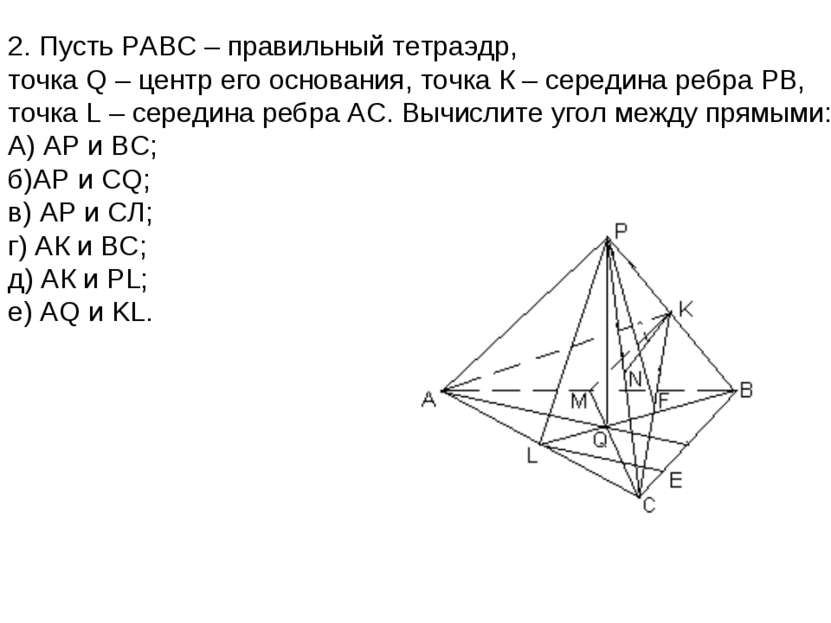
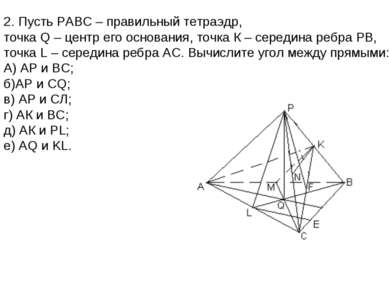
![; ; ; , ; ; , ; ] а) ((АР); (ВС)) = 900 б) ((АР); (СQ)) = KMС = arccos в) ((А...](https://bigslide.ru/images/39/38094/960/img8.jpg "; ; ; , ; ; , ; ] а) ((АР); (ВС)) = 900 б) ((АР); (СQ)) = KMС = arccos в) ((А...")
; ; ; , ; ; , ; ] а) ((АР); (ВС)) = 900 б) ((АР); (СQ)) = KMС = arccos в) ((АР); (СK)) = MKС = arccos г) ((АK); (BC)) = AKN = arccos д) = ((АK); (PL)) = PLF = arccos е) = ((АQ); (KL)) = KLE = arccos где E [BC] и |CE| = |BC|; BKE: KLE: где F – середина [CK]. PCK: PLF:
