X
Код презентации скопируйте его
Симметрия и движение (9 класс)
Скачать эту презентацию
Презентация на тему Симметрия и движение (9 класс)
Скачать эту презентациюCлайд 1
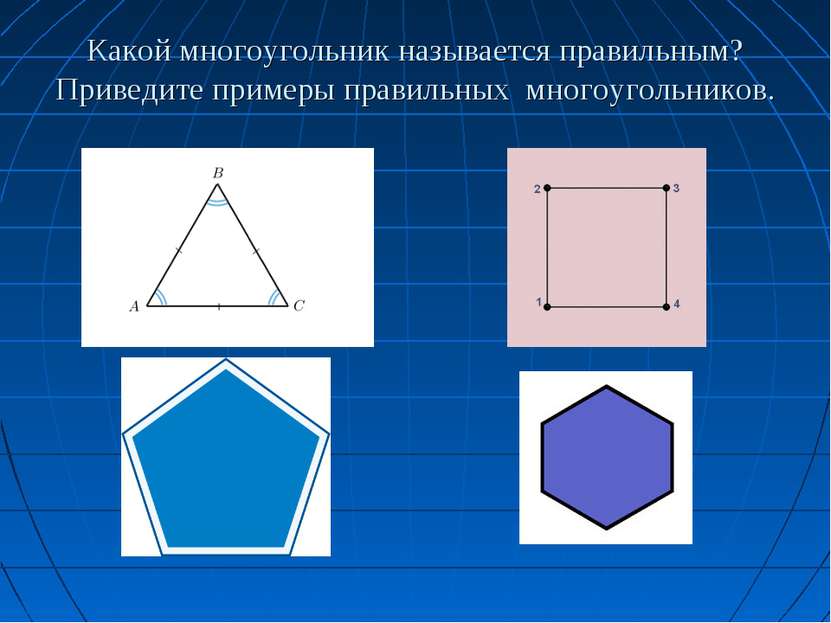
Со времён Пифагора известны они. В них равные стороны и равны углы. Их встретим в орнаментах и на паркетах В стихотворениях разных поэтов. И даже пчёлы с ними работают, Строя в их форме домики-соты. О. Панишева.
Cлайд 2
Cлайд 3
Какой многоугольник называется правильным? Приведите примеры правильных многоугольников.
Cлайд 4
Как найти сумму углов правильного многоугольника ? Как найти градусную величину внутреннего угла правильного выпуклого многоугольника? S = (n-2)180° (n-2)180°: n
Cлайд 5
Задача №1 Во дворе нашей школы есть клумба квадратной формы. Весной мы будем высаживать цветы на нашу клумбу. Сначала высаживать будем ландыши по окружности, которую можно вписать в квадратную клумбу. Затем тюльпаны в форме квадрата, вписанного в окружность. Сколько саженцев ландышей и клубней тюльпанов нужно высадить, если размеры клумбы 6х6 квадратных метров. Воспользоваться значением , . Высаживать цветы нужно через каждые 20 см.
Cлайд 6
Задача №2 Пчелиные соты представляют собой прямоугольник, покрытый правильными шестиугольниками. Найти, какими ещё правильными многоугольниками можно покрыть плоскость. Что для этого нужно знать?
Cлайд 7
Метод перебора. n=3. Три угла, плотно составленные, составляют 180°, шесть углов - 360°. Плоскость покрыта без просветов. n=4. Четыре внутренних угла вместе дают 360°, плоскость покрыта без просветов. n=5. Внутренний угол правильного многоугольника равен 108°, остаётся просвет в 36°. Плоскость без просветов не покрывается. n=6. Внутренний угол правильного шестиугольника равен 120°, три шестиугольника, составленные вместе, образуют 360°. Плоскость покрывается без просветов. Метод перебора можно продолжать и дальше, итогом будет служить вывод, чтобы без просветов плоскость можно покрыть лишь правильными треугольниками, квадратами, правильными шестиугольниками.
Cлайд 8
«Странные общественные привычки и геометрические дарования пчёл не могли не привлечь внимания и не вызвать восхищения людей, наблюдавших их жизнь и использовавших плоды их деятельности» Г. Вейль Почему пчёлы выбрали именно шестиугольник? ?
Cлайд 9
Решение Для ответа на этот вопрос нужно сравнить периметры разных многоугольников, имеющих одинаковую площадь. Пусть даны правильный треугольник, квадрат и правильный шестиугольник. У какого из этих многоугольников наименьший периметр? Пусть S- площадь каждой из названных фигур, сторона аn- соответствующего правильного n-угольника. Для сравнения периметров запишем их соотношение Р3 : Р4 : Р6 = 1 : 0,877 : 0,816 Мы видим, что из трёх правильных многоугольников с одинаковой площадью наименьший периметр имеет правильный шестиугольник. Стало быть, мудрые пчёлы, экономят воск и время для построения сот.
Cлайд 10
Некоторые итоги На этом математические секреты пчёл не заканчиваются. Интересно и дальше исследовать строение пчелиных сот. Расчётливые пчёлы заполняют пространство так, что не остаётся просветов, экономя при этом 2% воска. Как не согласиться с мнением Пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая геометрию моих сот». Так с помощью геометрии мы прикоснулись к тайне математических шедевров из воска, ещё раз убедившись во всесторонней эффективности математики.
Cлайд 11
Задача №3. Пол комнаты, имеющий форму прямоугольника со сторонами 5,5 м и 6 м, нужно покрыть паркетом прямоугольной формы. Длина каждой дощечки паркета равна 30 см, а ширина — 5 см. Сколько потребуется таких дощечек для покрытия пола?
Cлайд 12
Рефлексия: Что нового вы сегодня для себя узнали? Чему научились? Что давалось легко, а что вызывало затруднения? Где вы будете использовать данные ЗУНы? Какой информации было недостаточно при выполнении тех или иных заданий? Над чем стоит еще поработать дома?
