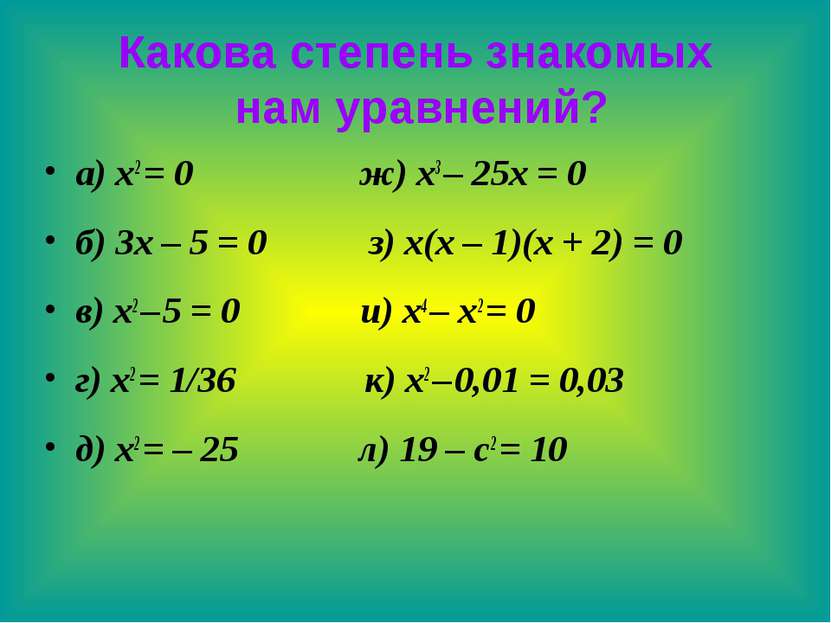X
Код презентации скопируйте его
Целое уравнение и его корни
Скачать эту презентациюПрезентация на тему Целое уравнение и его корни
Скачать эту презентациюCлайд 1
 Алгебра 9 класс Учитель: Романова Т.А. 20 октября 2008 год МОУ Надеждинская средняя общеобразовательная школа Кошкинского района Самарской области
Алгебра 9 класс Учитель: Романова Т.А. 20 октября 2008 год МОУ Надеждинская средняя общеобразовательная школа Кошкинского района Самарской области
Cлайд 2
 Решить устно уравнения а) x2 = 0 ж) x3 – 25x = 0 б) 3x – 5 = 0 з) x(x – 1)(x + 2) = 0 в) x2 – 5 = 0 и) x4 – x2 = 0 г) x2 = 1/36 к) x2 – 0,01 = 0,03 д) x2 = – 25 л) 19 – c2 = 10 е) = 0 м) (x – 3)2 = 25 1) х – 3 = 5 и 2) х – 3 = – 5 Какие из этих уравнений не являются целыми?
Решить устно уравнения а) x2 = 0 ж) x3 – 25x = 0 б) 3x – 5 = 0 з) x(x – 1)(x + 2) = 0 в) x2 – 5 = 0 и) x4 – x2 = 0 г) x2 = 1/36 к) x2 – 0,01 = 0,03 д) x2 = – 25 л) 19 – c2 = 10 е) = 0 м) (x – 3)2 = 25 1) х – 3 = 5 и 2) х – 3 = – 5 Какие из этих уравнений не являются целыми?
Cлайд 4
 Основная цель урока: Обобщить и систематизировать знания о целых уравнениях и методах их решений.
Основная цель урока: Обобщить и систематизировать знания о целых уравнениях и методах их решений.
Cлайд 5
 Целые уравнения Уравнения, в которых левая и правая часть являются целыми выражениями называются целыми уравнениями. Степенью целого уравнения называют степень равносильного ему уравнения вида Р(х) = 0, где Р(х) – многочлен стандартного вида Какова степень знакомых нам уравнений?
Целые уравнения Уравнения, в которых левая и правая часть являются целыми выражениями называются целыми уравнениями. Степенью целого уравнения называют степень равносильного ему уравнения вида Р(х) = 0, где Р(х) – многочлен стандартного вида Какова степень знакомых нам уравнений?
Cлайд 6
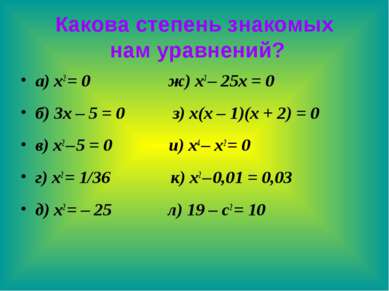 Какова степень знакомых нам уравнений? а) x2 = 0 ж) x3 – 25x = 0 б) 3x – 5 = 0 з) x(x – 1)(x + 2) = 0 в) x2 – 5 = 0 и) x4 – x2 = 0 г) x2 = 1/36 к) x2 – 0,01 = 0,03 д) x2 = – 25 л) 19 – c2 = 10
Какова степень знакомых нам уравнений? а) x2 = 0 ж) x3 – 25x = 0 б) 3x – 5 = 0 з) x(x – 1)(x + 2) = 0 в) x2 – 5 = 0 и) x4 – x2 = 0 г) x2 = 1/36 к) x2 – 0,01 = 0,03 д) x2 = – 25 л) 19 – c2 = 10
Cлайд 7
 Целые уравнения В учебнике найдите № 205. Посмотрите на уравнения а), б) и в). Чем они отличаются? Уравнения будем решать аналитическим способом. С чего начнём?
Целые уравнения В учебнике найдите № 205. Посмотрите на уравнения а), б) и в). Чем они отличаются? Уравнения будем решать аналитическим способом. С чего начнём?
Cлайд 8
 Целые уравнения Решите уравнения: 2∙х + 5 =15 0∙х = 7 Сколько корней может иметь уравнение I степени? Не более одного!
Целые уравнения Решите уравнения: 2∙х + 5 =15 0∙х = 7 Сколько корней может иметь уравнение I степени? Не более одного!
Cлайд 9
 Целые уравнения Решите уравнения: I вариант II вариант III вариант x2-5x+6=0 y2-4y+7=0 x2-12x+36=0 D=1, D>0, D=-12, D
Целые уравнения Решите уравнения: I вариант II вариант III вариант x2-5x+6=0 y2-4y+7=0 x2-12x+36=0 D=1, D>0, D=-12, D
Cлайд 10
 Целые уравнения Решите уравнения: I вариант II вариант III вариант x3-1=0 x3- 4x=0 x3-12x2+36x=0 x3=1 x(x2- 4)=0 x(x2-12x+36)=0 x=1 x=0, x=2, x= -2 x=0, x=6 1 корень 3 корня 2 корня Сколько корней может иметь уравнение I I I степени? Не более трех!
Целые уравнения Решите уравнения: I вариант II вариант III вариант x3-1=0 x3- 4x=0 x3-12x2+36x=0 x3=1 x(x2- 4)=0 x(x2-12x+36)=0 x=1 x=0, x=2, x= -2 x=0, x=6 1 корень 3 корня 2 корня Сколько корней может иметь уравнение I I I степени? Не более трех!
Cлайд 11
 Целые уравнения Как вы думаете сколько корней может иметь уравнение IV, V , VI, VII, n-й степени? Не более четырёх, пяти, шести, семи корней! Вообще не более n корней !
Целые уравнения Как вы думаете сколько корней может иметь уравнение IV, V , VI, VII, n-й степени? Не более четырёх, пяти, шести, семи корней! Вообще не более n корней !
Cлайд 12
 Целые уравнения Мы с вами сегодня решали уравнения аналитическим способом, но существует не только этот способ. Прежде чем с ним познакомится вспомним известные нам функции и их графики!
Целые уравнения Мы с вами сегодня решали уравнения аналитическим способом, но существует не только этот способ. Прежде чем с ним познакомится вспомним известные нам функции и их графики!
Cлайд 13
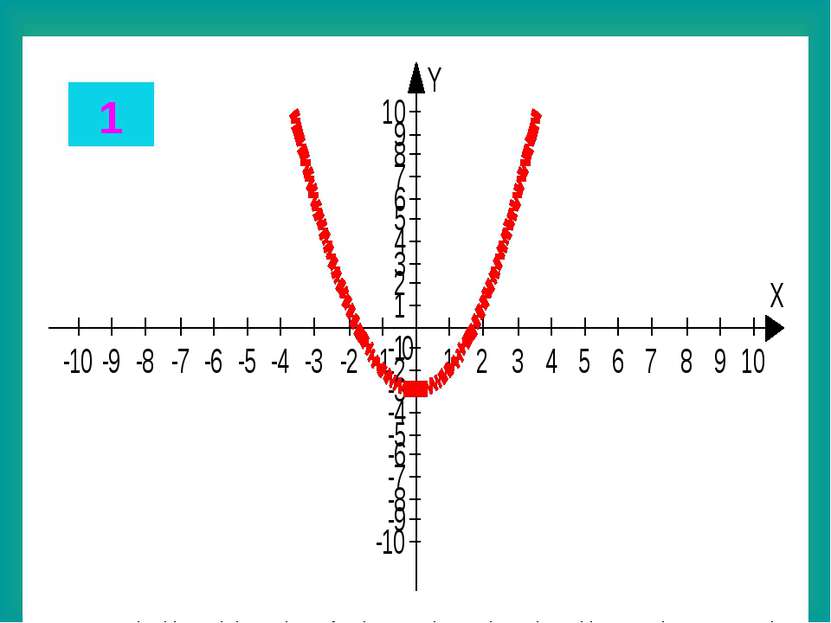
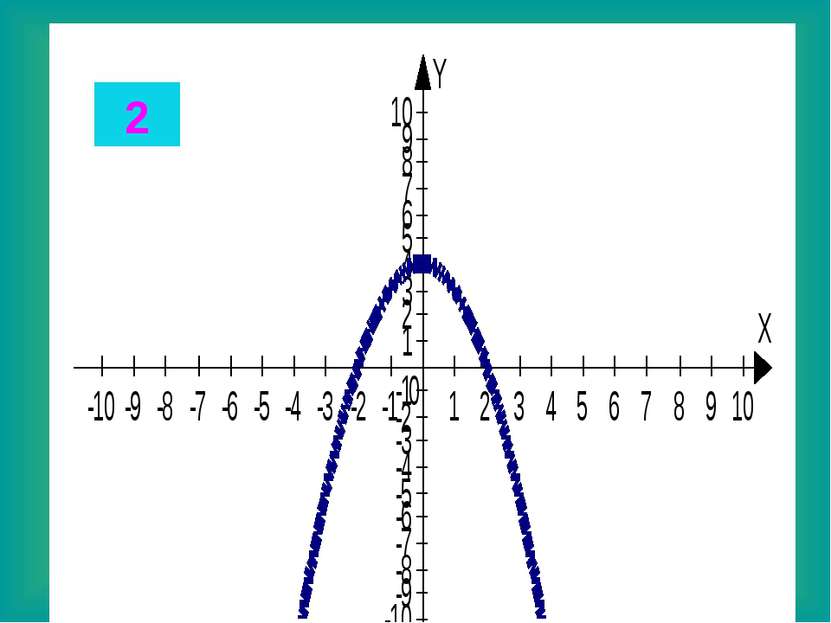
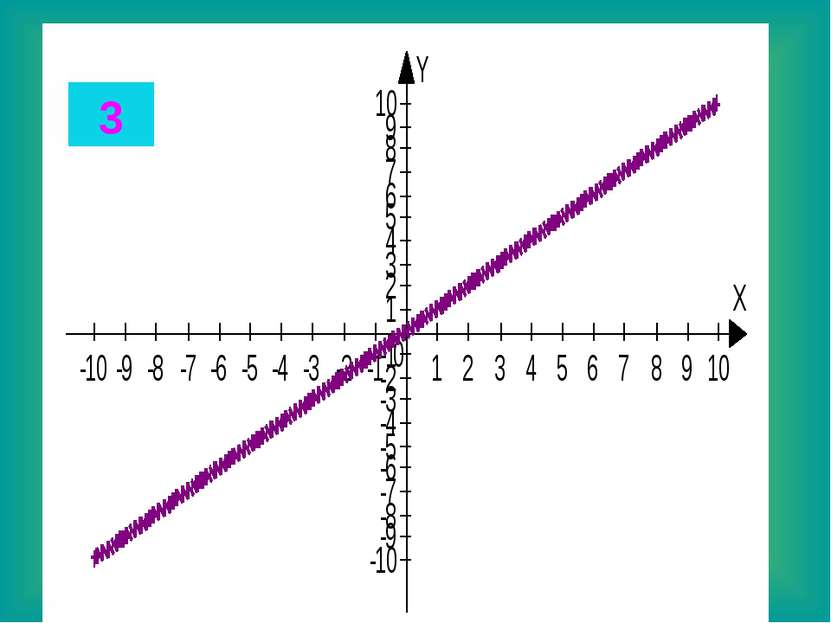
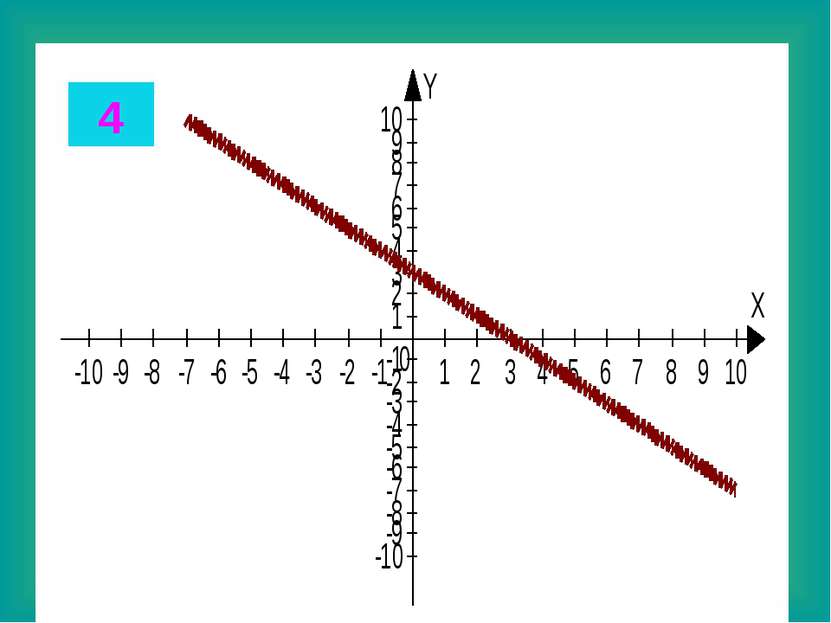
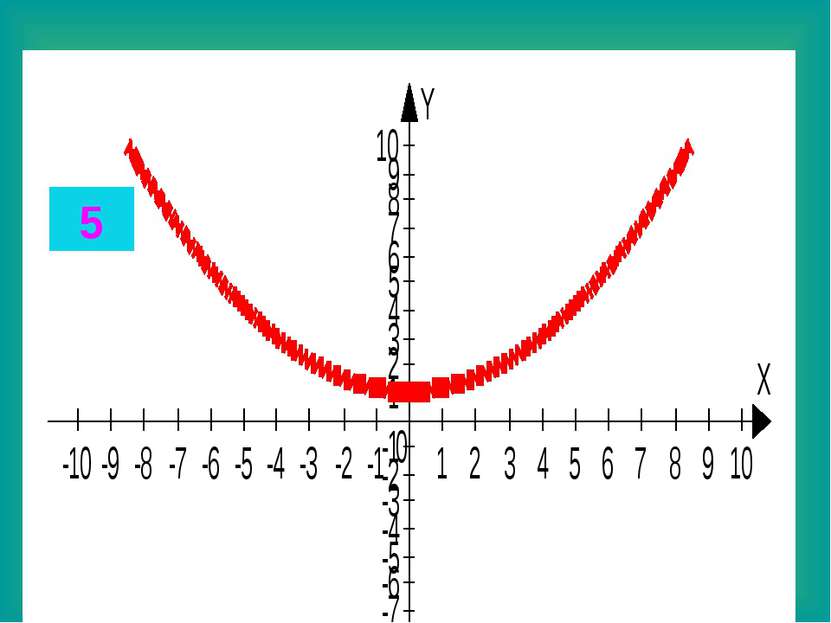
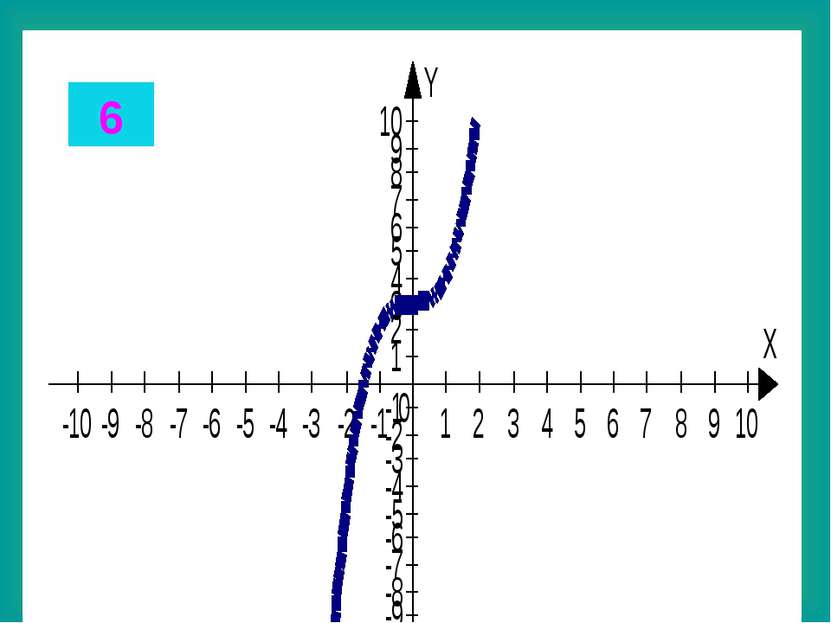
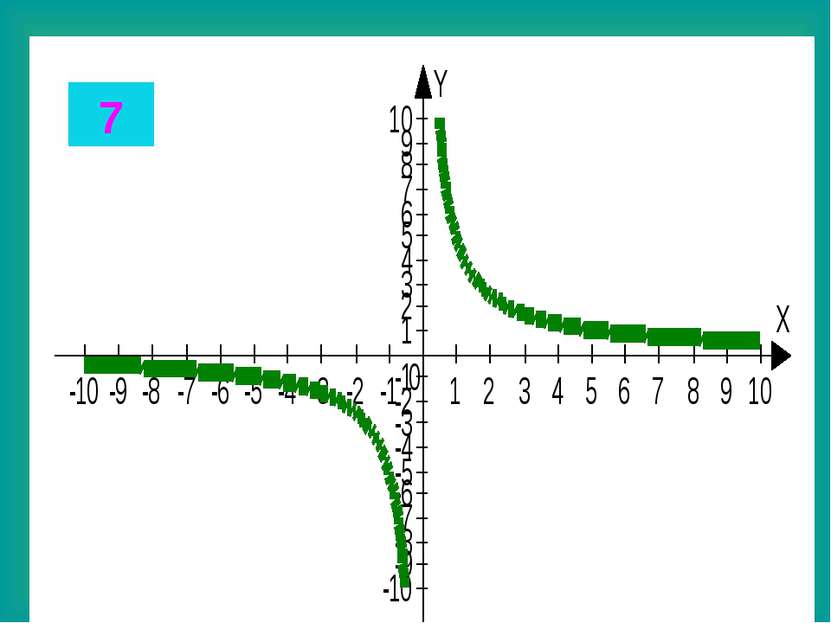
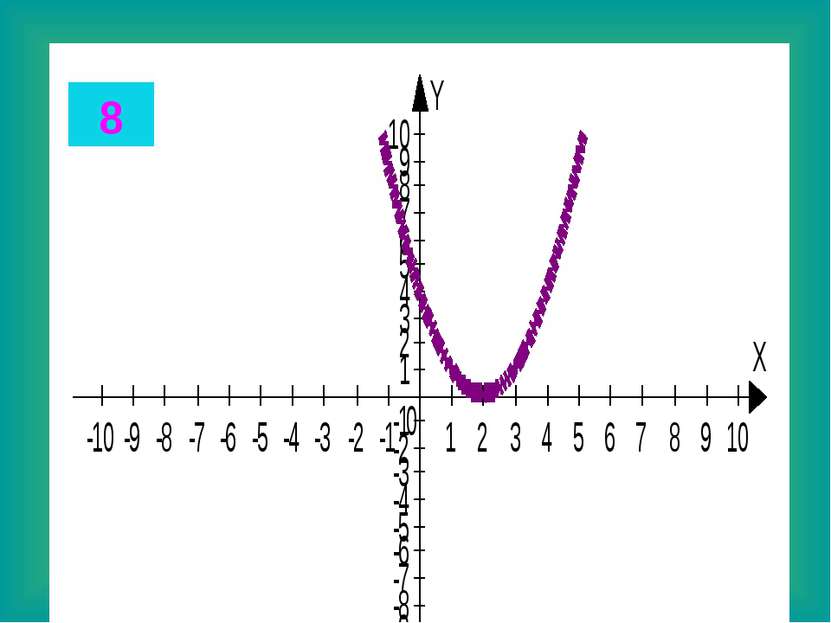
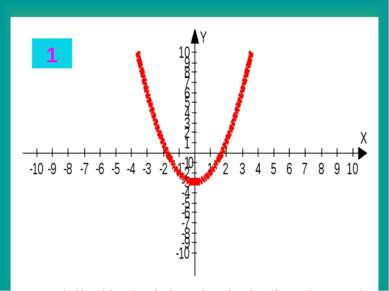
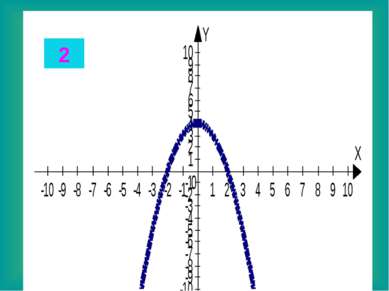
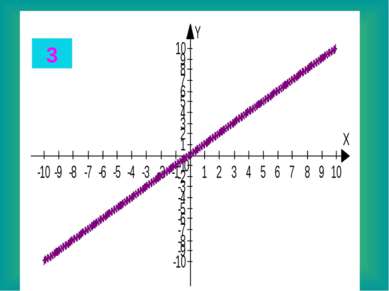
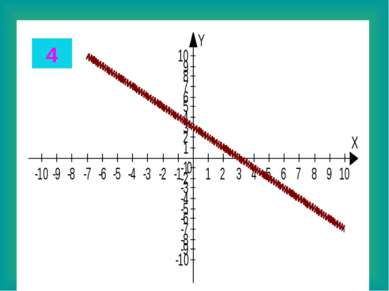
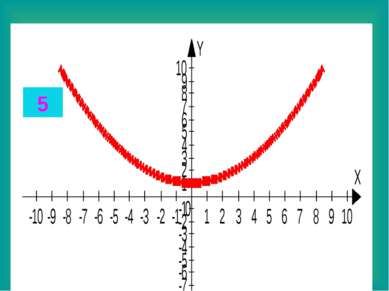
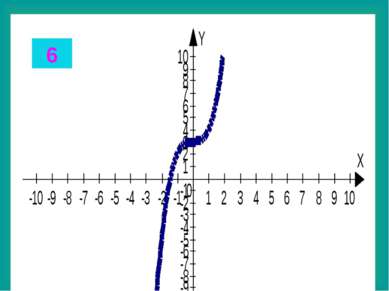
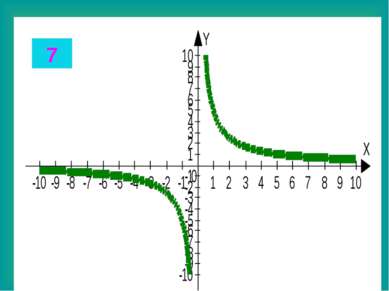
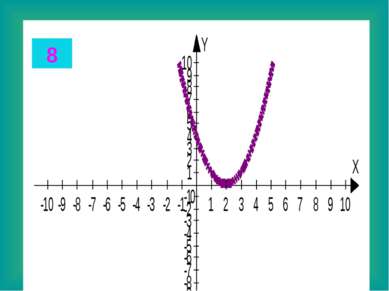
 Целые уравнения Из списка функций приведенного на доске выберите функцию, соответствующую данному графику. Запишите в тетради данные соответствия
Целые уравнения Из списка функций приведенного на доске выберите функцию, соответствующую данному графику. Запишите в тетради данные соответствия
Cлайд 22
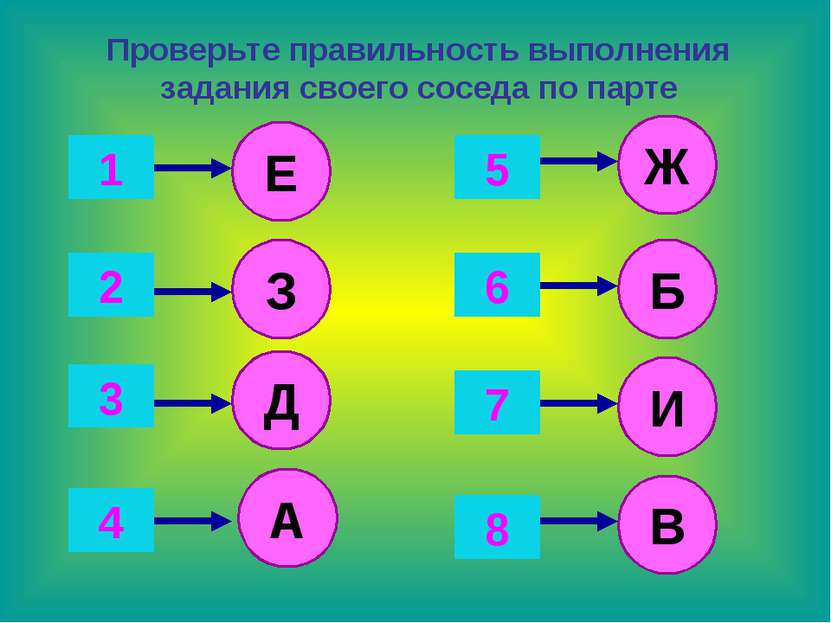
 1 2 3 4 5 6 7 Проверьте правильность выполнения задания своего соседа по парте 8 Е А З Д Ж Б И В
1 2 3 4 5 6 7 Проверьте правильность выполнения задания своего соседа по парте 8 Е А З Д Ж Б И В
Cлайд 23
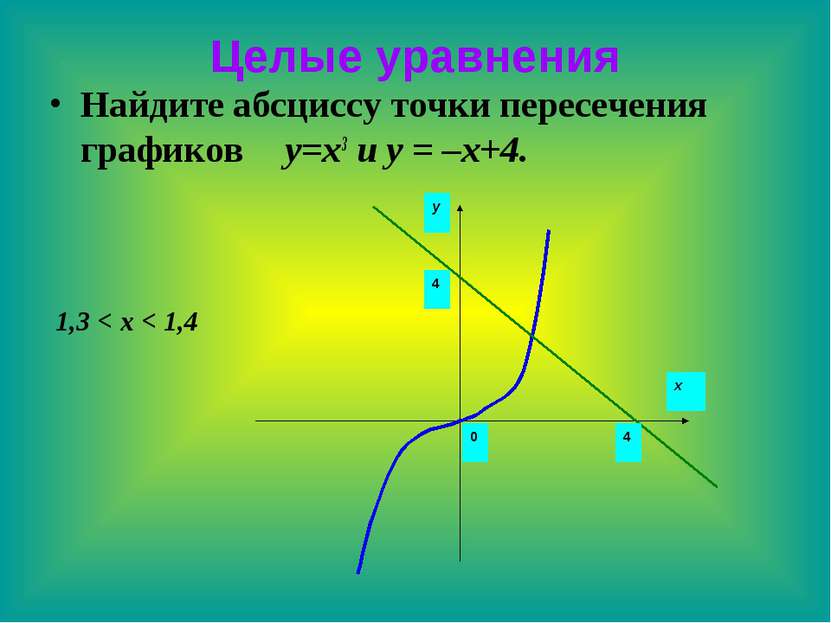
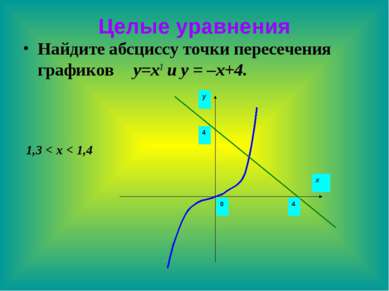
 Целые уравнения А сейчас рассмотрим еще один (графический) способ решение уравнения I I I степени? Уравнение x3 + x – 4 = 0. А сколько корней оно может иметь? Запишем это уравнение в виде x3 = –x + 4. Рассмотрим функции y=x3 и y = –x+4. Что является графиками данных функций? Кубическая парабола и прямая. См. рисунок № 43 учебника (Алгебра 9 класс),
Целые уравнения А сейчас рассмотрим еще один (графический) способ решение уравнения I I I степени? Уравнение x3 + x – 4 = 0. А сколько корней оно может иметь? Запишем это уравнение в виде x3 = –x + 4. Рассмотрим функции y=x3 и y = –x+4. Что является графиками данных функций? Кубическая парабола и прямая. См. рисунок № 43 учебника (Алгебра 9 класс),
Cлайд 25
 Попробуйте назвать корень данного уравнения! Как вы думаете, в чём недостаток данного метода решения? Да, графический способ решения уравнений не всегда обеспечивает высокую точность результата, и поэтому иногда приходится этот результат уточнять при помощи вычислений. Итак, ребята, данное уравнение имеет 1 решение х ≈ 1,37
Попробуйте назвать корень данного уравнения! Как вы думаете, в чём недостаток данного метода решения? Да, графический способ решения уравнений не всегда обеспечивает высокую точность результата, и поэтому иногда приходится этот результат уточнять при помощи вычислений. Итак, ребята, данное уравнение имеет 1 решение х ≈ 1,37
Cлайд 26
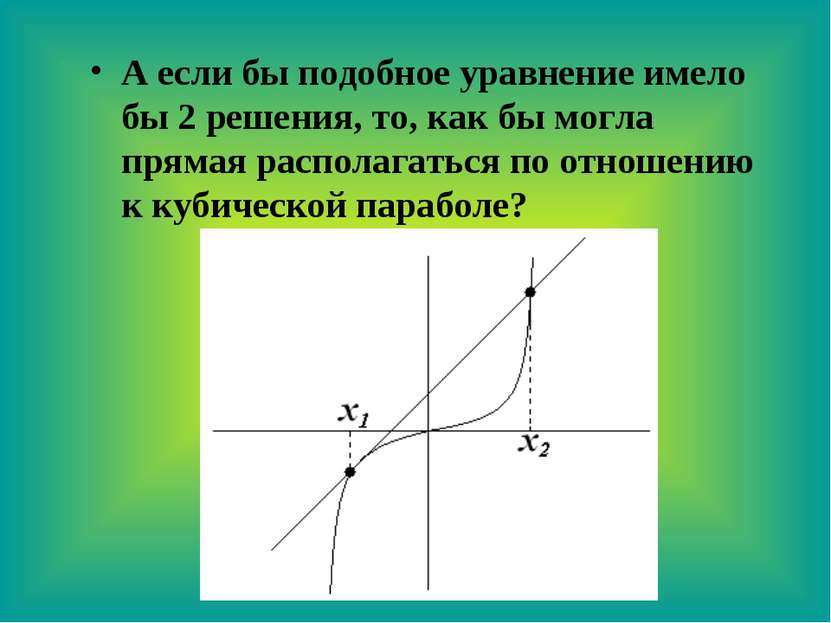
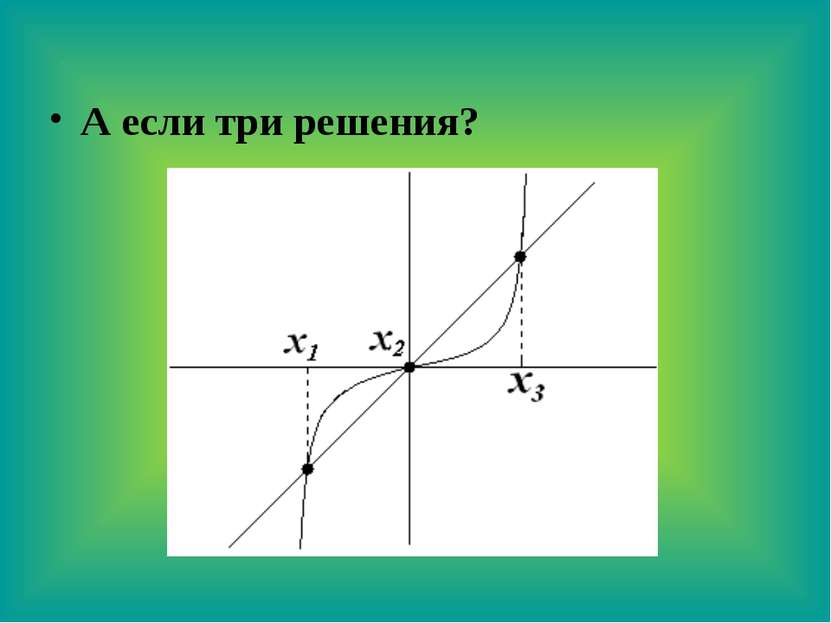
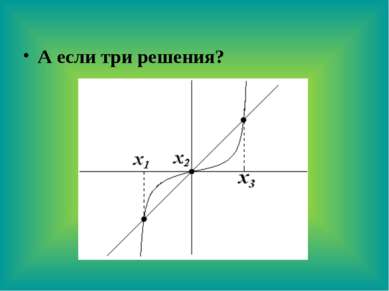
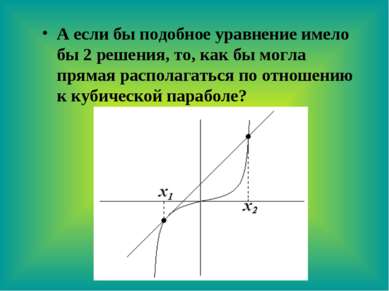 А если бы подобное уравнение имело бы 2 решения, то, как бы могла прямая располагаться по отношению к кубической параболе?
А если бы подобное уравнение имело бы 2 решения, то, как бы могла прямая располагаться по отношению к кубической параболе?
Cлайд 28
 Рассмотрите пример решения уравнения графическим способом Чтобы решить уравнение х2 + 2х – 8 =0 представим его в виде х2 = – 2х +8, Далее рассмотрим функции у = х2 и у = – 2х +8. Что является графиком каждой функции? Построим графики этих функций в одной системе координат. Определим абсциссы точек пересечения, они будут являться корнями нашего уравнения
Рассмотрите пример решения уравнения графическим способом Чтобы решить уравнение х2 + 2х – 8 =0 представим его в виде х2 = – 2х +8, Далее рассмотрим функции у = х2 и у = – 2х +8. Что является графиком каждой функции? Построим графики этих функций в одной системе координат. Определим абсциссы точек пересечения, они будут являться корнями нашего уравнения
Cлайд 29
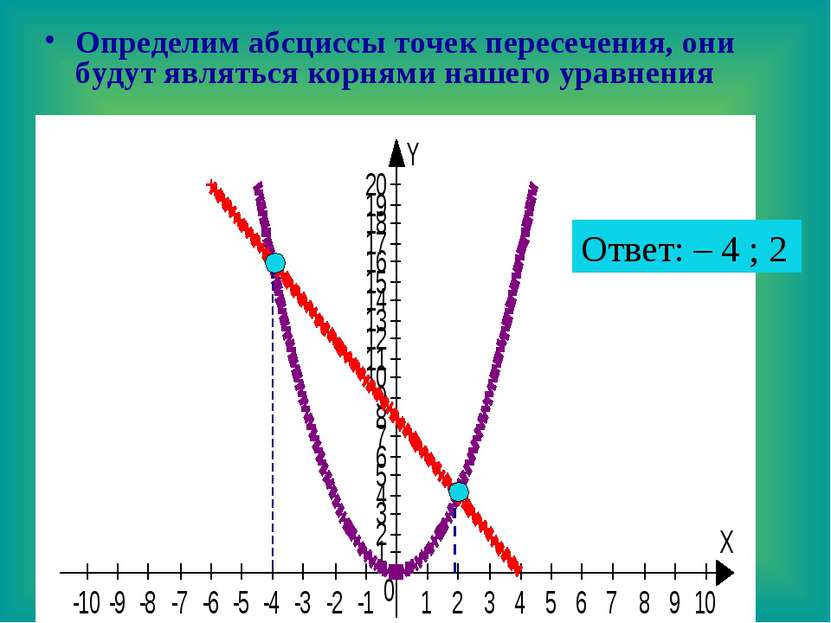
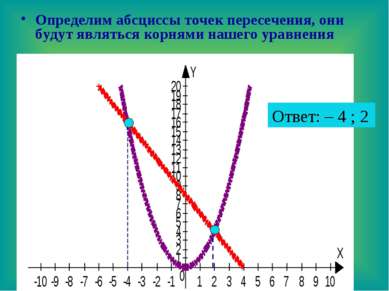 Определим абсциссы точек пересечения, они будут являться корнями нашего уравнения Ответ: – 4 ; 2
Определим абсциссы точек пересечения, они будут являться корнями нашего уравнения Ответ: – 4 ; 2