X
Код презентации скопируйте его
Задачи на построение
Скачать эту презентацию
Презентация на тему Задачи на построение
Скачать эту презентациюCлайд 1
Cлайд 2
Введение Геометрические инструменты школьника и инженера 1.Линейка. 2.Циркуль. 3.Транспортир.
Cлайд 3
Набор инструментов
Cлайд 4
Набор инструментов
Cлайд 5
Cлайд 6
В геометрии выделяют задачи на построение, которые можно решить только с помощью двух инструментов: циркуля и линейки без масштабных делений. Линейка позволяет провести произвольную прямую, а также построить прямую, проходящую через две данные точки; с помощью циркуля можно провести окружность произвольного радиуса, а также окружность с центром в данной точке и радиусом, равным данному отрезку. IIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIIII
Cлайд 7
План решения задачи на построение. Анализ ( нахождение связи между элементами геометрической фигуры). Построение с обязательным описанием хода его выполнения. Доказательство получения искомой фигуры. Исследование.
Cлайд 8
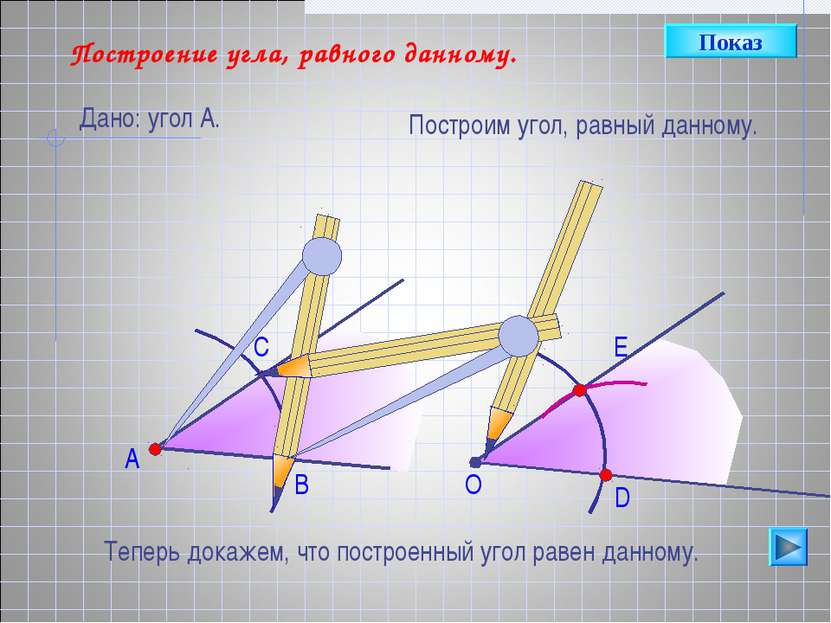
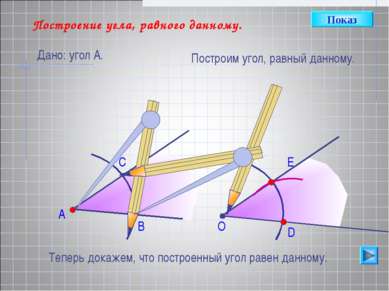А В С Построение угла, равного данному. Дано: угол А. Построим угол, равный данному. О D E Теперь докажем, что построенный угол равен данному. Показ
Cлайд 9
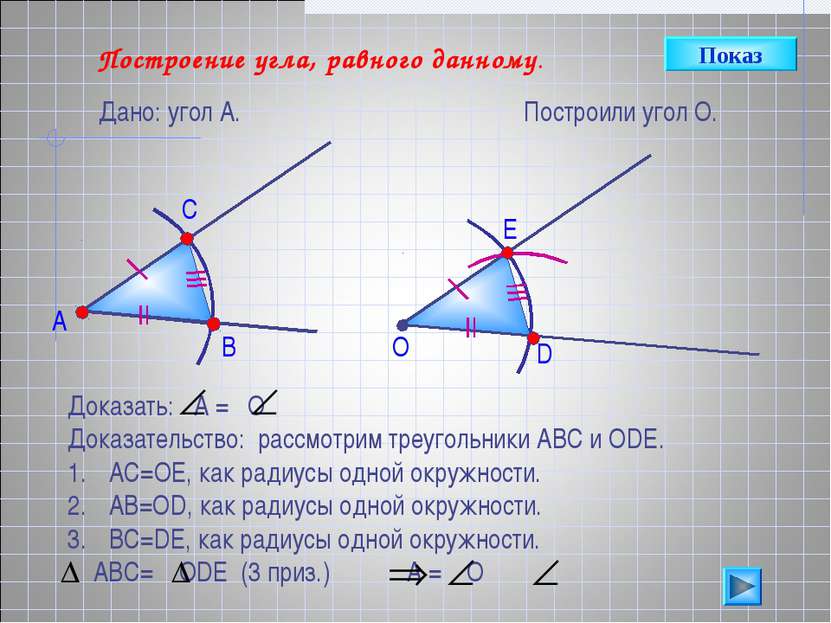
Построение угла, равного данному. Дано: угол А. А Построили угол О. В С О D E Доказать: А = О Доказательство: рассмотрим треугольники АВС и ОDE. АС=ОЕ, как радиусы одной окружности. АВ=ОD, как радиусы одной окружности. ВС=DE, как радиусы одной окружности. АВС= ОDЕ (3 приз.) А = О Показ
Cлайд 10
биссектриса Построение биссектрисы угла. Показ
Cлайд 11
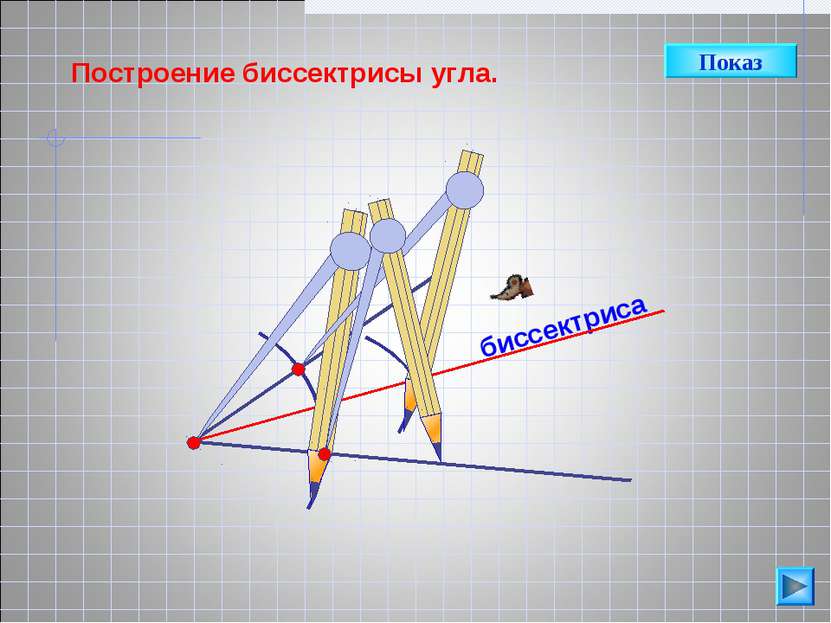
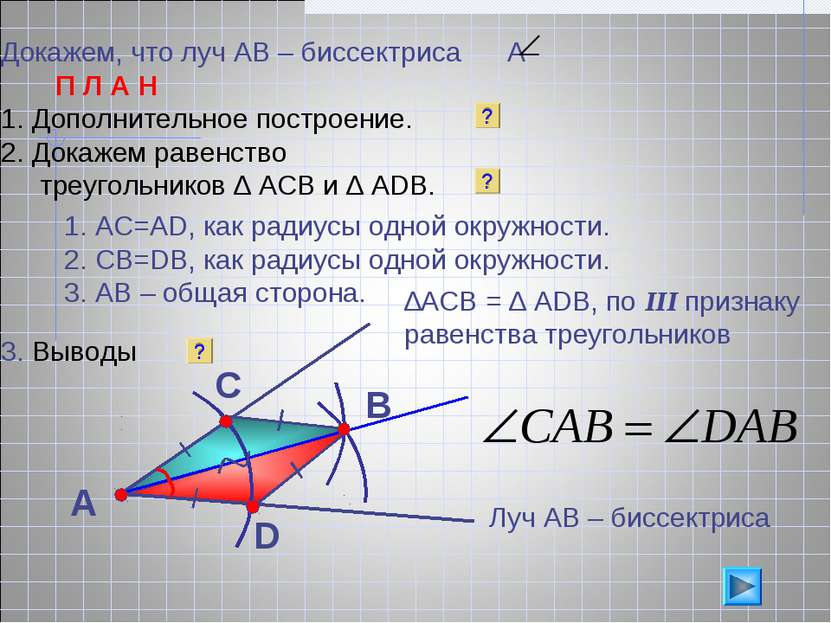
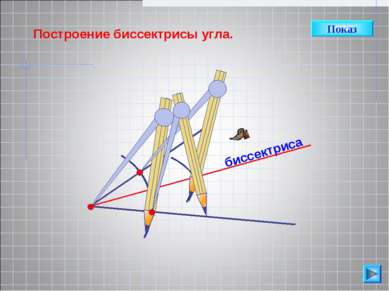
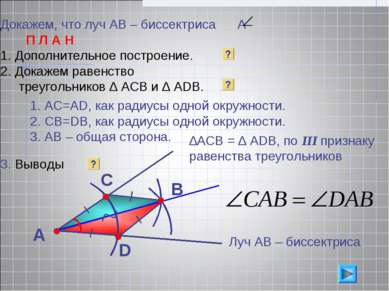Докажем, что луч АВ – биссектриса А П Л А Н Дополнительное построение. Докажем равенство треугольников ∆ АСВ и ∆ АDB. 3. Выводы А В С D АС=АD, как радиусы одной окружности. СВ=DB, как радиусы одной окружности. АВ – общая сторона. ? ∆АСВ = ∆ АDВ, по III признаку равенства треугольников Луч АВ – биссектриса ? ?
Cлайд 12
В А Показ Построение перпендикулярных прямых.
Cлайд 13
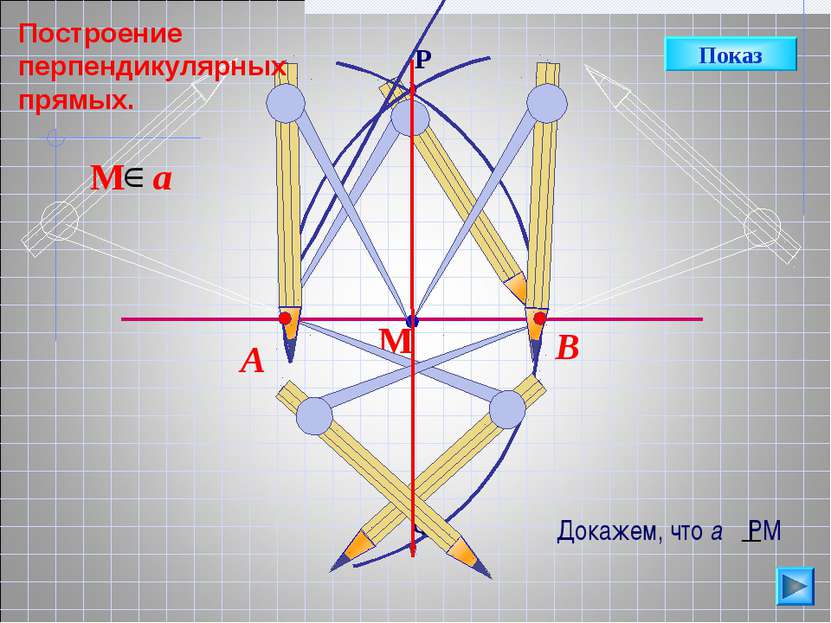
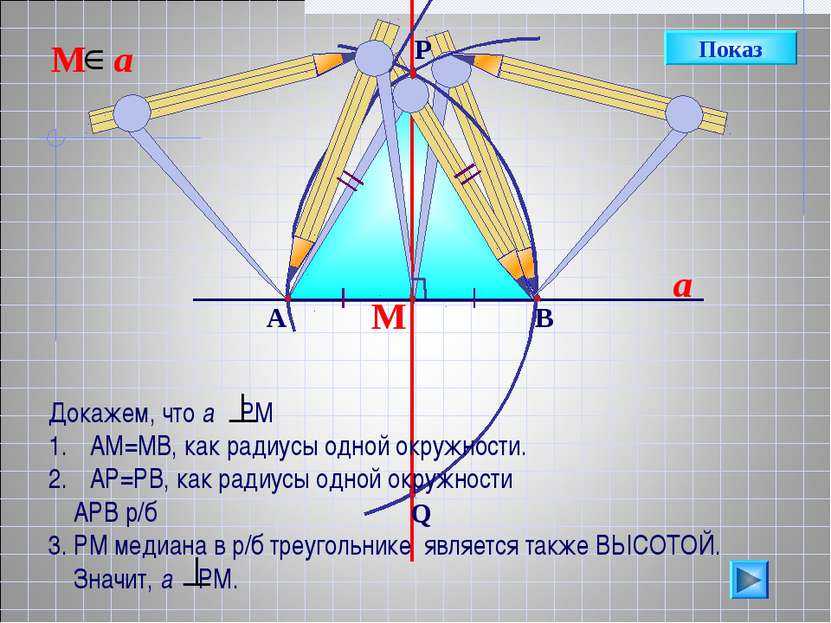
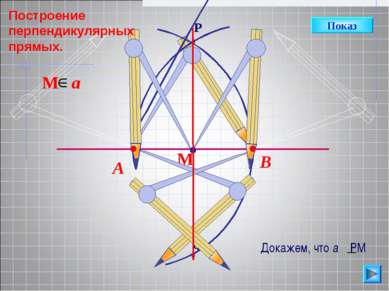
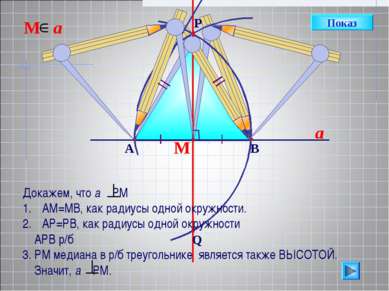М a Докажем, что а РМ АМ=МВ, как радиусы одной окружности. АР=РВ, как радиусы одной окружности АРВ р/б 3. РМ медиана в р/б треугольнике является также ВЫСОТОЙ. Значит, а РМ. Показ
Cлайд 14
a N М Построение перпендикулярных прямых. Показ
Cлайд 15
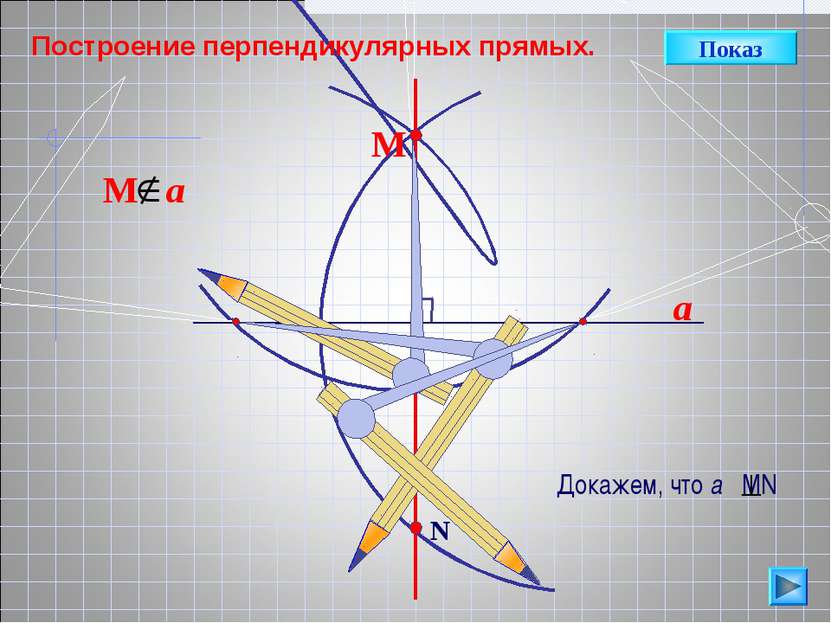
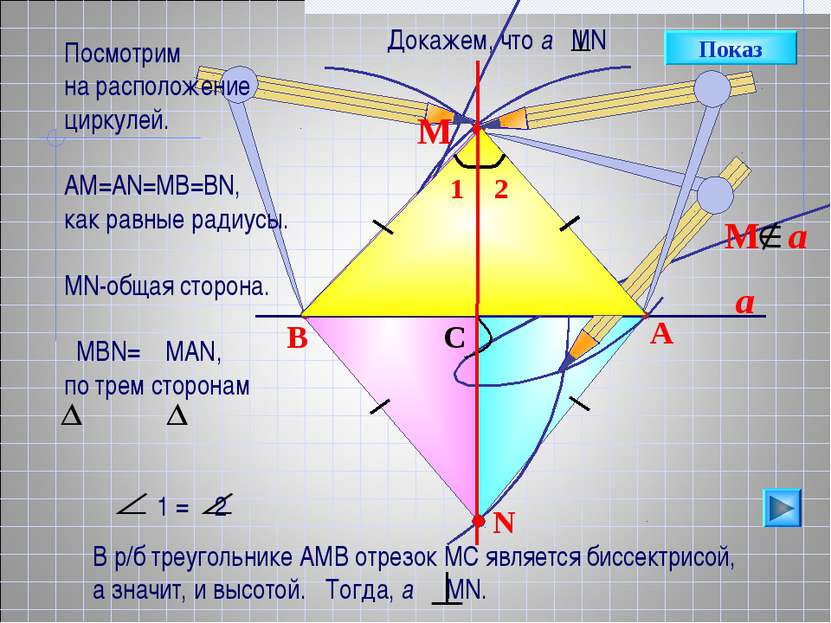
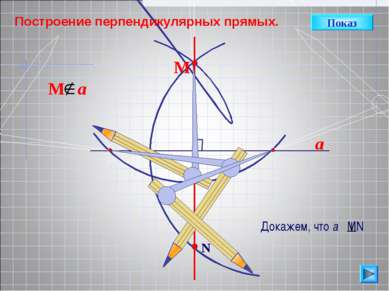
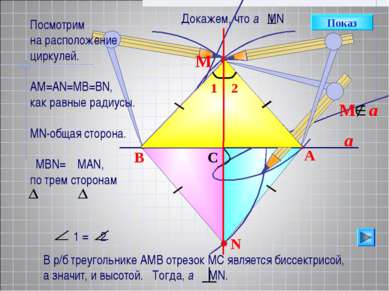a N B A C М Показ Посмотрим на расположение циркулей. АМ=АN=MB=BN, как равные радиусы. МN-общая сторона. MВN= MAN, по трем сторонам
Cлайд 16
Докажем, что О – середина отрезка АВ. Показ Построение середины отрезка
Cлайд 17
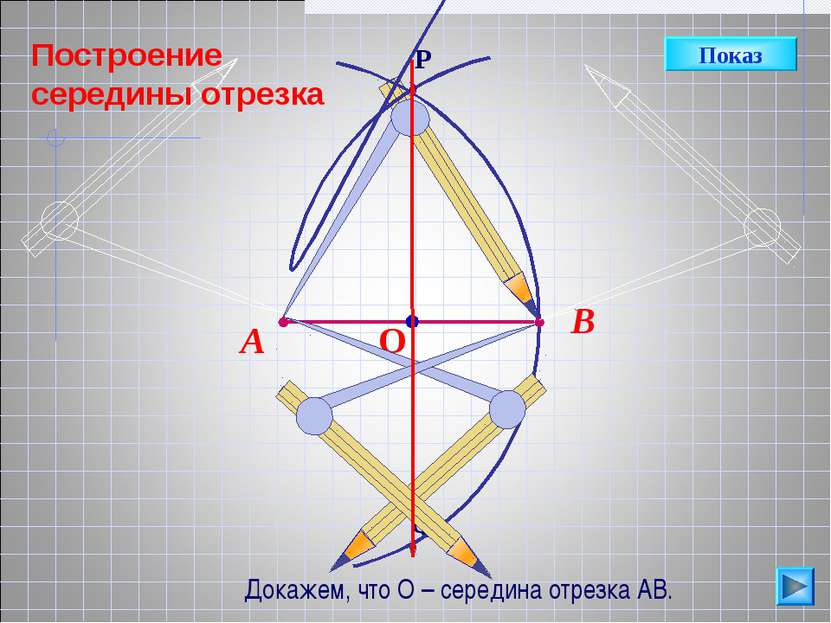
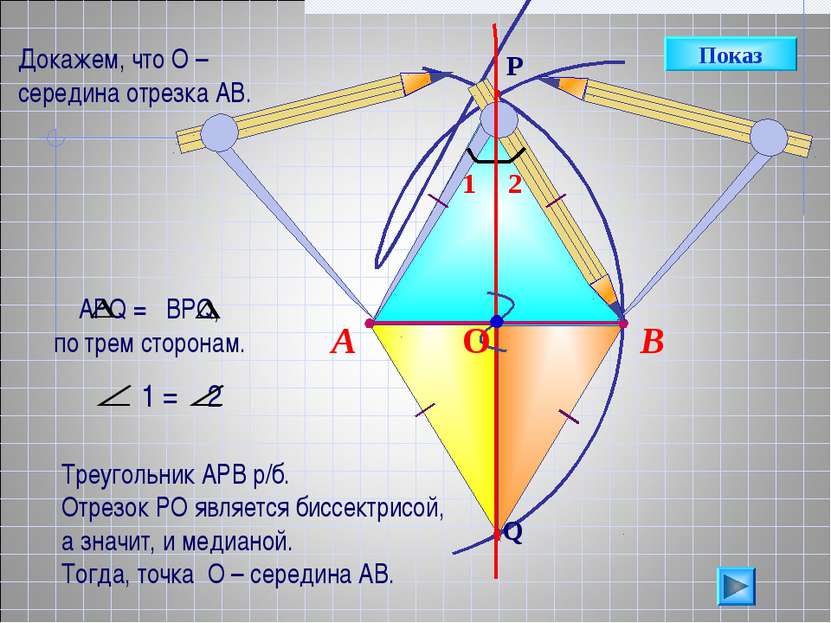
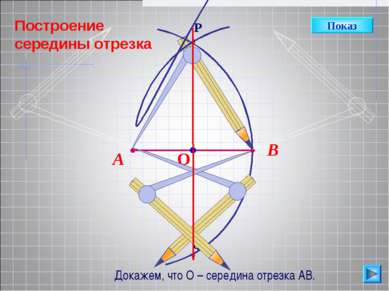
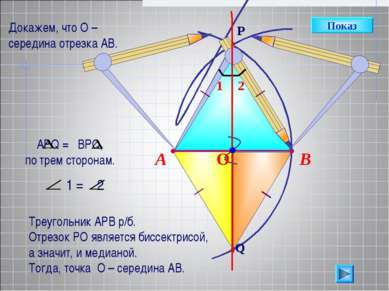В А Треугольник АРВ р/б. Отрезок РО является биссектрисой, а значит, и медианой. Тогда, точка О – середина АВ. Показ Докажем, что О – середина отрезка АВ.
Cлайд 18
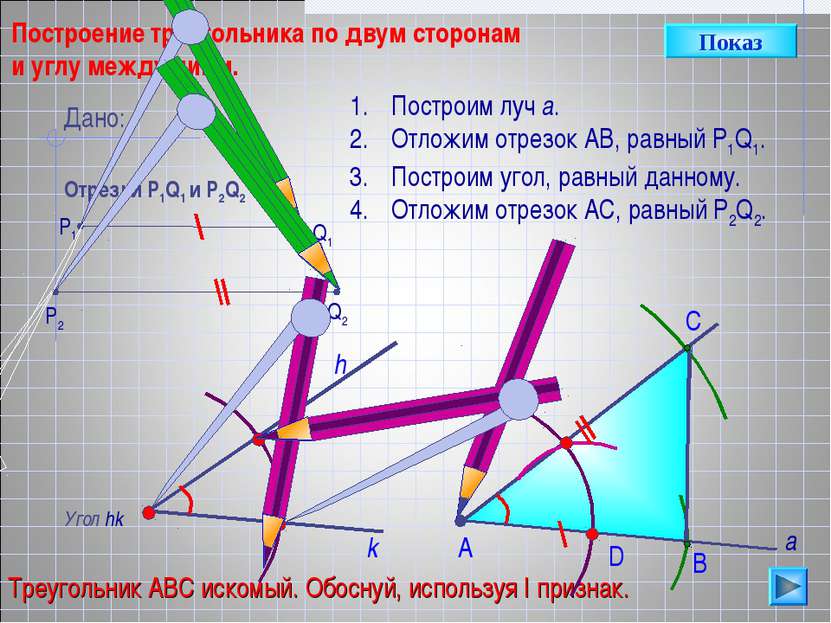
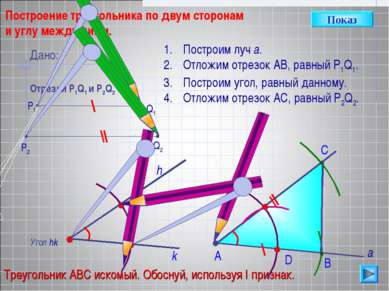D С Построение треугольника по двум сторонам и углу между ними. Угол hk h Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим угол, равный данному. Отложим отрезок АС, равный P2Q2. В А Треугольник АВС искомый. Обоснуй, используя I признак. Дано: Отрезки Р1Q1 и Р2Q2 Q1 P1 P2 Q2 а k Показ
Cлайд 19
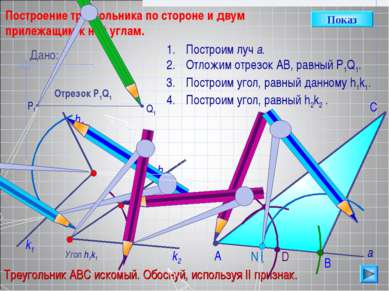D С Построение треугольника по стороне и двум прилежащим к ней углам. Угол h1k1 h2 Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим угол, равный данному h1k1. Построим угол, равный h2k2 . В А Треугольник АВС искомый. Обоснуй, используя II признак. Дано: Отрезок Р1Q1 Q1 P1 а k2 Показ h1 k1 N
Cлайд 20
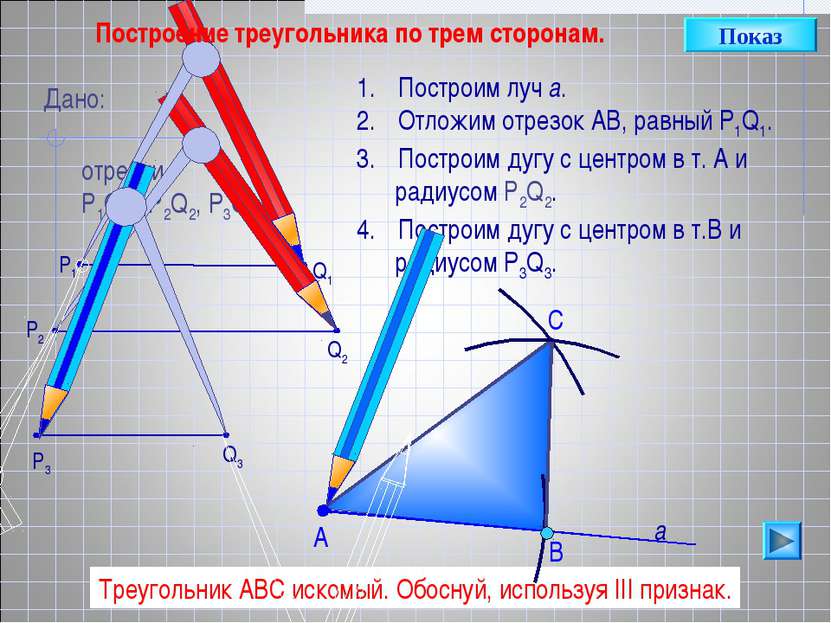
С Построим луч а. Отложим отрезок АВ, равный P1Q1. Построим дугу с центром в т. А и радиусом Р2Q2. Построим дугу с центром в т.В и радиусом P3Q3. В А Треугольник АВС искомый. Обоснуй, используя III признак. Дано: отрезки Р1Q1, Р2Q2, P3Q3. Q1 P1 P3 Q2 а P2 Q3 Показ Построение треугольника по трем сторонам.
Cлайд 21
Методы решения задач на построение 1.Метод анализа. 2.Метод подобия. 3.Метод геометрических мест.
Cлайд 22
НЕРАЗРЕШИМЫЕ ЗАДАЧИ Квадратура круга - построение квадрата , равновеликого данному кругу с помощью циркуля и линейки
Cлайд 23
НЕРАЗРЕШИМЫЕ НЕРАЗРЕШИМЫЕ ЗАДАЧИ ТРИСЕКЦИЯ УГЛА – деление данного угла на три равных части с помощью циркуля и линейки.
Cлайд 24
НЕРАЗРЕШИМЫЕ ЗАДАЧИ УДВОЕНИЕ КУБА – построение ребра куба , объем которого вдвое больше объема данного куба, с помощью циркуля и линейки.
Cлайд 25
СПАСИБО ЗА ВНИМАНИЕ! ДО ВСТРЕЧИ В БУДУЩЕМ УЧЕБНОМ ГОДУ!
