X
Код презентации скопируйте его
Первообразная 11 класс
Скачать эту презентацию
Презентация на тему Первообразная 11 класс
Скачать эту презентациюCлайд 1
Учитель: Савичева Наталья Геннадьевна ЦО 109 Москва, 2013 Первообразная и интеграл
Cлайд 2
Первообразная Функция F(x) называется первообразной для функции f(x) на данном промежутке, если для любого x из этого промежутка F’(x) = f(x). Пример: Первообразной для функции f(x)=x на всей числовой оси является F(x)=x2/2, поскольку (x2/2)’=x.
Cлайд 3
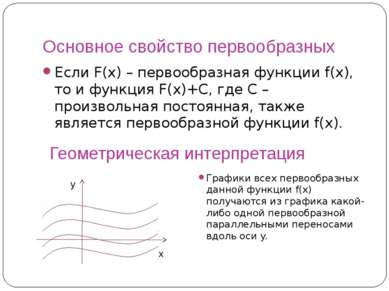Основное свойство первообразных Если F(x) – первообразная функции f(x), то и функция F(x)+C, где C – произвольная постоянная, также является первообразной функции f(x). Графики всех первообразных данной функции f(x) получаются из графика какой-либо одной первообразной параллельными переносами вдоль оси y. Геометрическая интерпретация y x
Cлайд 4
Неопределенный интеграл Совокупность всех первообразных данной функции f(x) называется ее неопределенным интегралом и обозначается : , где C – произвольная постоянная.
Cлайд 5
Правила интегрирования
Cлайд 6
Определенный интеграл В декартовой прямоугольной системе координат XOY фигура, ограниченная осью OX, прямыми x=a, x=b (a
Cлайд 7
Определенный интеграл Вычислим площадь криволинейной трапеции. Разобьем отрезок [a;b] на n равных частей. Проведем через полученные точки прямые, параллельные оси OY. Заданная криволинейная трапеция разобьется на n частей. Площадь всей трапеции приближенно равна сумме площадей столбиков. по определению , его называют определенным интегралом от функции y=f(x) по отрезку [a;b] и обозначают так:
Cлайд 8
Связь между определенным интегралом и первообразной (Формула Ньютона - Лейбница) Для непрерывной функции где F(x) – первообразная функции f(x).
Cлайд 9
Основные свойства определенного интеграла
Cлайд 10
Основные свойства определенного интеграла
Cлайд 11
Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:
Cлайд 12
Геометрический смысл определенного интеграла Площадь криволинейной трапеции, ограниченной графиком непрерывной отрицательной на промежутке [a;b] функции f(x), осью x и прямыми x=a и x=b:
Cлайд 13
Геометрический смысл определенного интеграла Замечание: Если функция изменяет знак на промежутке [a;b] , то
Cлайд 14
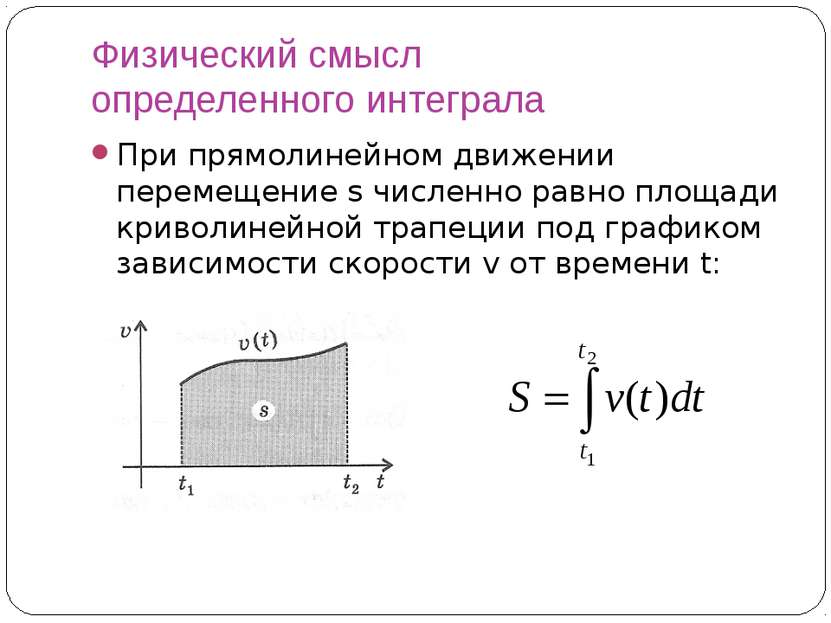
Физический смысл определенного интеграла При прямолинейном движении перемещение s численно равно площади криволинейной трапеции под графиком зависимости скорости v от времени t:
Cлайд 15
с помощью определенного интеграла Вычисление площадей и объемов
Cлайд 16
Площадь фигуры, Ограниченной графиками непрерывных функций y=f(x) и y=g(x) таких, что для любого x из [a;b], где a и b – абсциссы точек пересечения графиков функций:
Cлайд 17
Объем тела, полученного в результате вращения вокруг оси x криволинейной трапеции, ограниченной графиком непрерывной и неотрицательной функции y=f(x) на отрезке [a;b]:
