X
Код презентации скопируйте его
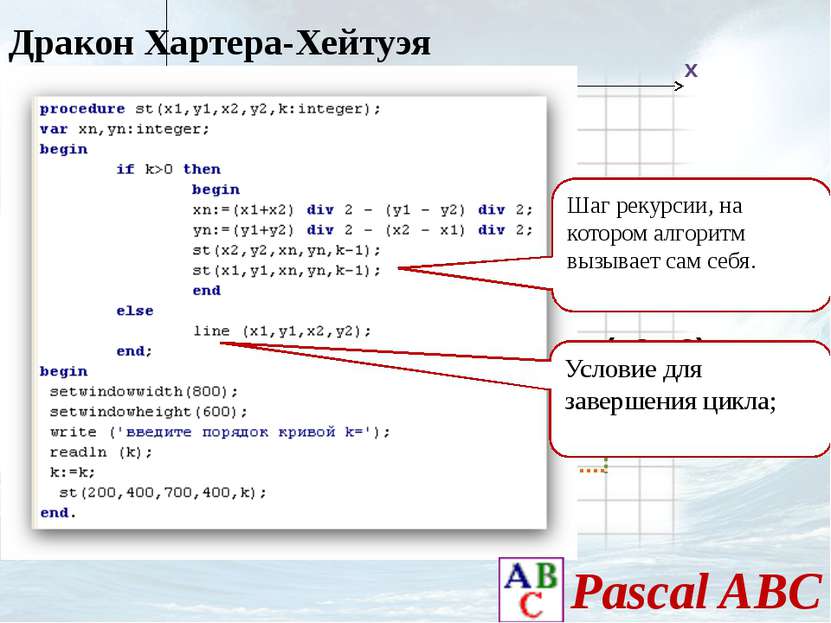
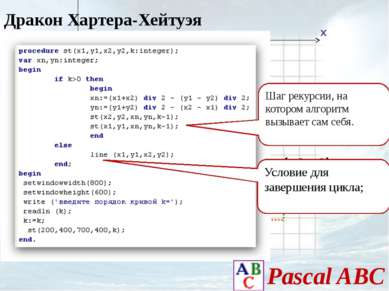
Построение геометрических фракталов методом рекурсии
Скачать эту презентациюПрезентация на тему Построение геометрических фракталов методом рекурсии
Скачать эту презентациюCлайд 2
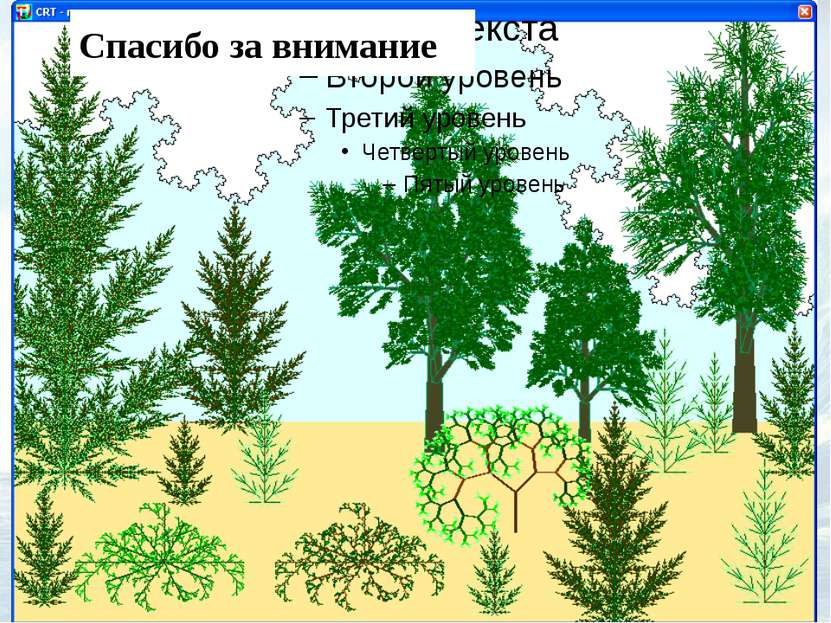
 "Почему геометрию часто называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - это не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой... природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности". Бенуа Мандельброт (1924-2010)
"Почему геометрию часто называют холодной и сухой? Одна из причин заключается в её неспособности описать форму облака, горы, дерева или берега моря. Облака - это не сферы, горы - это не конусы, линии берега - это не окружности, и кора не является гладкой, и молния не распространяется по прямой... природа демонстрирует нам не просто более высокую степень, а совсем другой уровень сложности". Бенуа Мандельброт (1924-2010)
Cлайд 3
 Пыль Кантора Первые идеи фрактальной геометрии возникли в 19 веке. Один из старейших фракталов - множество Кантора Суммарная длина удаленных отрезков равна 1. Суммарная длина получившихся в пределе отрезков равна нулю. Георг Кантор (1845-1918)
Пыль Кантора Первые идеи фрактальной геометрии возникли в 19 веке. Один из старейших фракталов - множество Кантора Суммарная длина удаленных отрезков равна 1. Суммарная длина получившихся в пределе отрезков равна нулю. Георг Кантор (1845-1918)
Cлайд 4
 Снежинка Коха “Странные” кривые с необычным “поведением” Любой, даже ничтожно малый отрезок кривой в точности повторяет по свойствам саму кривую. Хельге фон Кох (1870-1924)
Снежинка Коха “Странные” кривые с необычным “поведением” Любой, даже ничтожно малый отрезок кривой в точности повторяет по свойствам саму кривую. Хельге фон Кох (1870-1924)
Cлайд 5
 Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Рождение фрактальной геометрии связывают с выходом в 1977 году книги Б. Мандельброта Средствами традиционной геометрии (то есть, используя линии и поверхности), чрезвычайно сложно представить природные объекты. Фрактальная геометрия задает их очень просто.
Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому. Рождение фрактальной геометрии связывают с выходом в 1977 году книги Б. Мандельброта Средствами традиционной геометрии (то есть, используя линии и поверхности), чрезвычайно сложно представить природные объекты. Фрактальная геометрия задает их очень просто.
Cлайд 6
 Рекурсия — частичное определение объекта через себя, определение объекта с использованием ранее определённых. Рекурсия используется, когда можно выделить самоподобие задачи. Рекурсия
Рекурсия — частичное определение объекта через себя, определение объекта с использованием ранее определённых. Рекурсия используется, когда можно выделить самоподобие задачи. Рекурсия