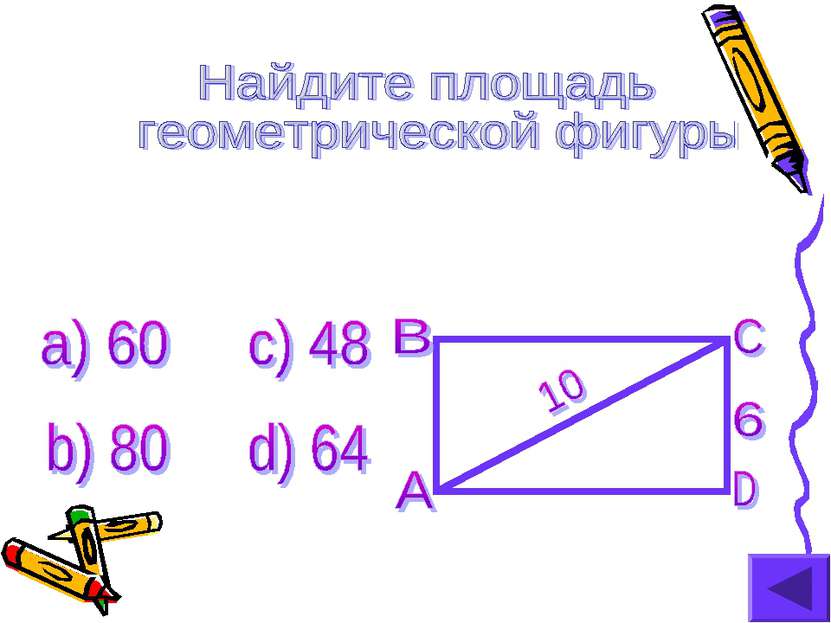
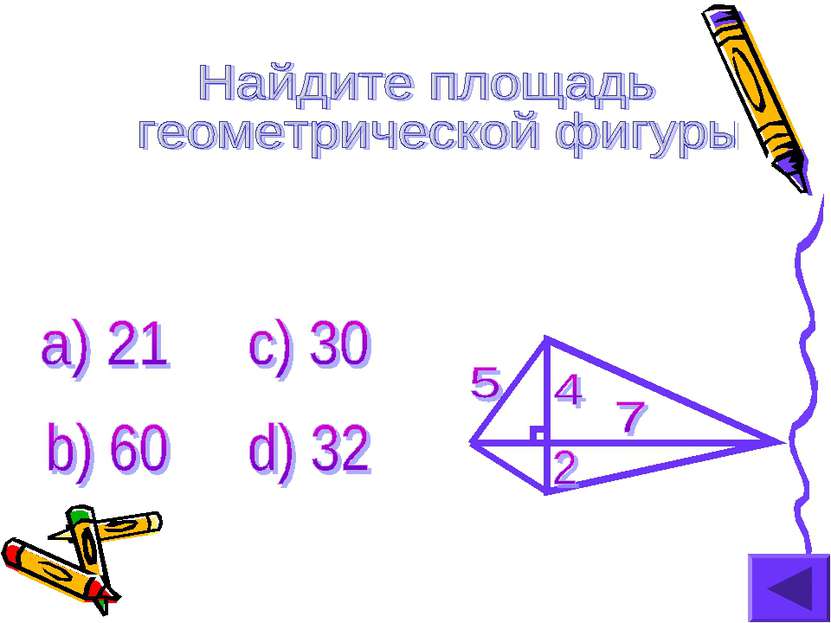
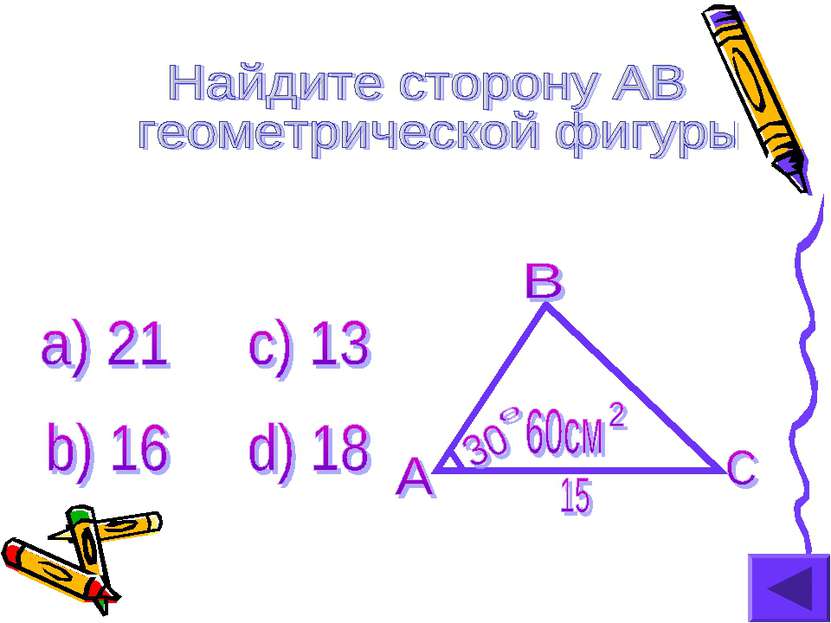
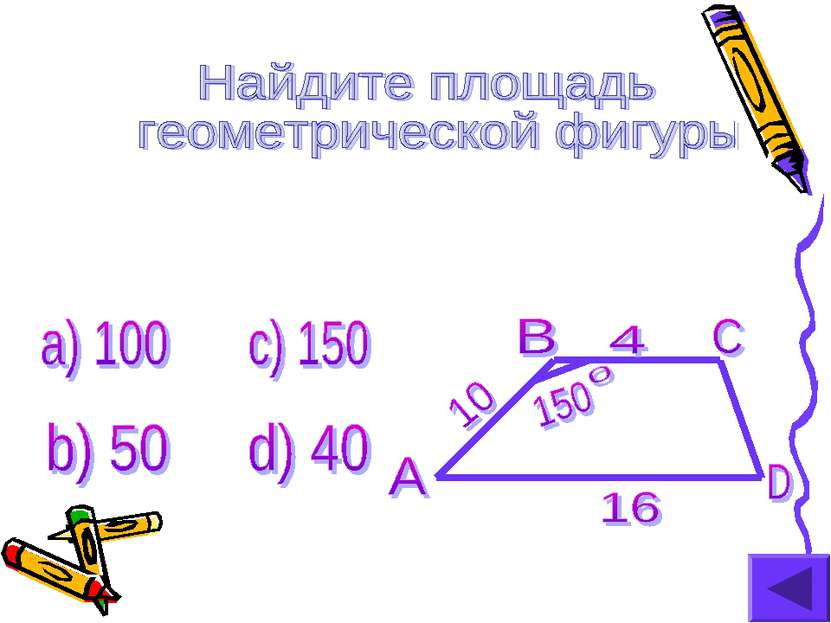
X
Код презентации скопируйте его
Площади фигур
Скачать эту презентацию
Презентация на тему Площади фигур
Скачать эту презентациюCлайд 1
Cлайд 2
Основные свойства площадей геометрических фигур. Площадь квадрата. Площадь прямоугольника. Площадь параллелограмма. Площадь треугольника. Площадь треугольника. Площадь трапеции. ТЕСТ. Список литературы.
Cлайд 3
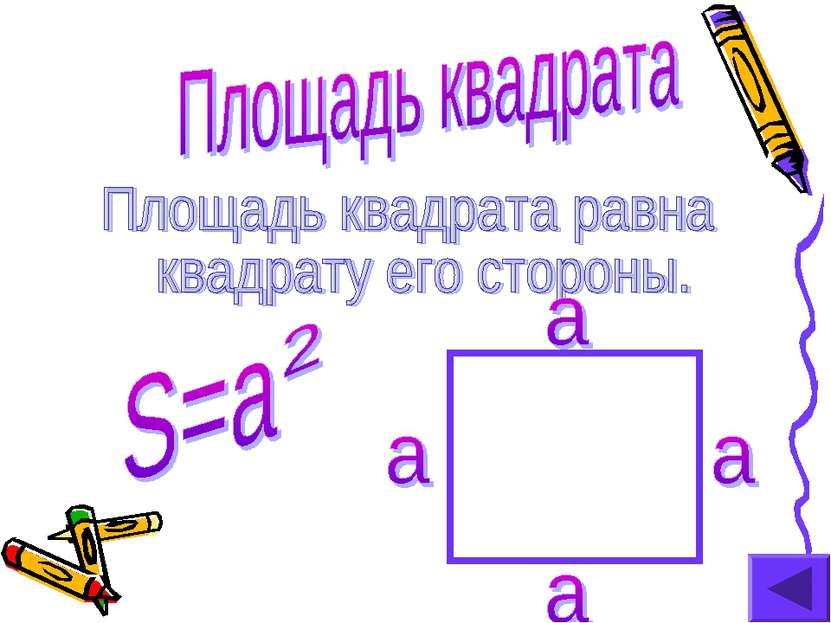
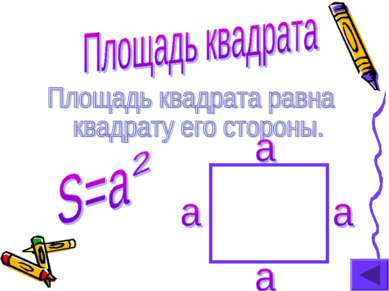
Любая плоская геометрическая фигура имеет площадь. Эта площадь – единственная. Площадь любой геометрической фигуры выражается положительным числом. Площадь квадрата со стороной,равной единице,равна единице. Площадь фигуры равна сумме площадей частей,на которые она разбивается. Равные многоугольники имеют равные площади.
Cлайд 4
Cлайд 5
Cлайд 6
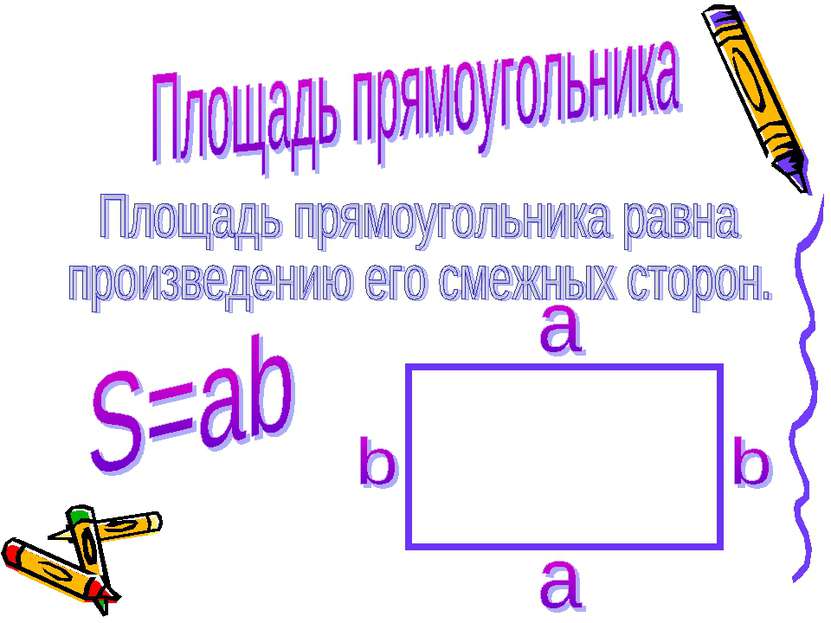
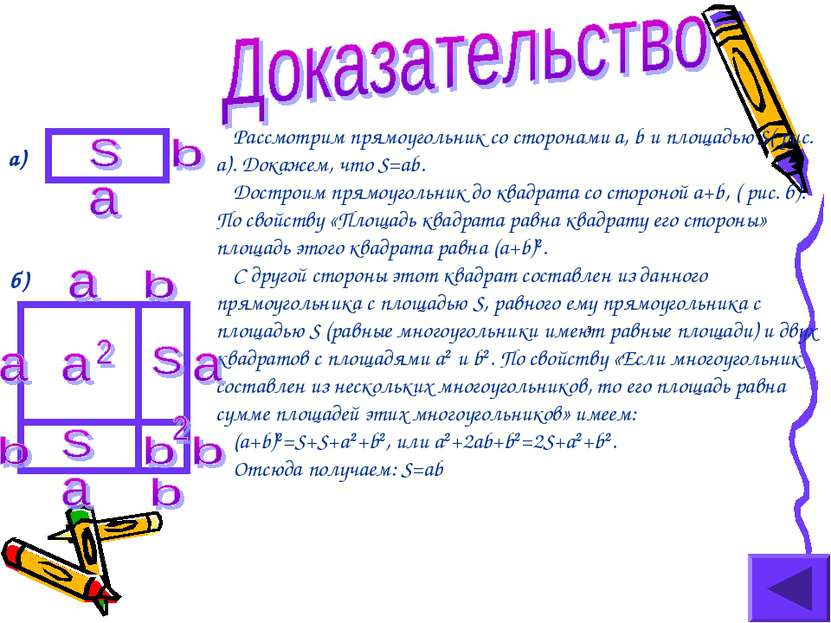
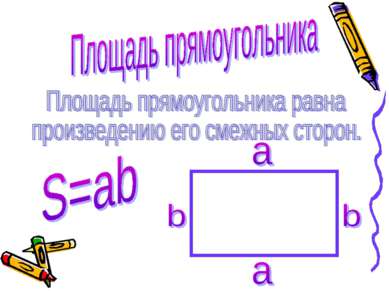
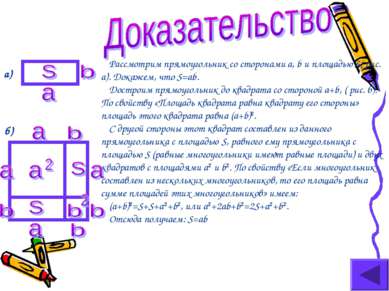Рассмотрим прямоугольник со сторонами a, b и площадью S( рис. а). Докажем, что S=ab. Достроим прямоугольник до квадрата со стороной a+b, ( рис. б). По свойству «Площадь квадрата равна квадрату его стороны» площадь этого квадрата равна (a+b)2. С другой стороны этот квадрат составлен из данного прямоугольника с площадью S, равного ему прямоугольника с площадью S (равные многоугольники имеют равные площади) и двух квадратов с площадями a2 и b2. По свойству «Если многоугольник составлен из нескольких многоугольников, то его площадь равна сумме площадей этих многоугольников» имеем: (a+b)2=S+S+a2+b2, или a2+2ab+b2=2S+a2+b2. Отсюда получаем: S=ab а) б)
Cлайд 7
Cлайд 8
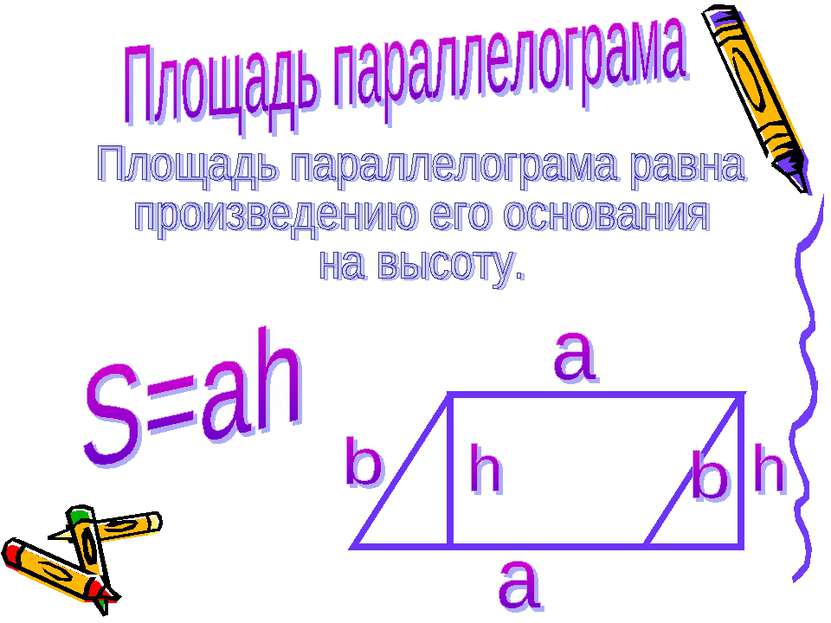
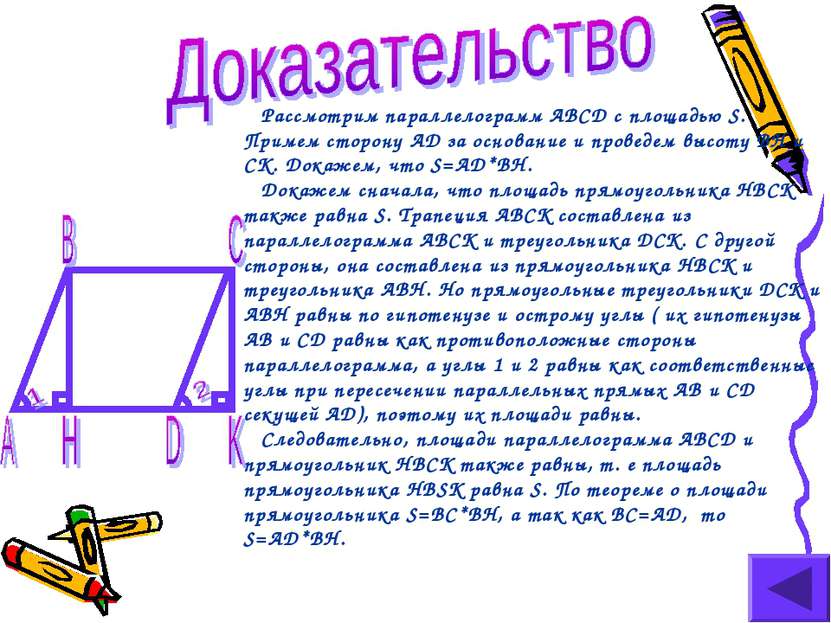
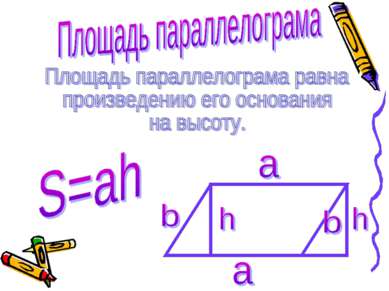
Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD за основание и проведем высоту BH и CK. Докажем, что S=AD*BH. Докажем сначала, что площадь прямоугольника HBCK также равна S. Трапеция ABCK составлена из параллелограмма ABCK и треугольника DCK. С другой стороны, она составлена из прямоугольника HBCK и треугольника ABH. Но прямоугольные треугольники DCK и ABH равны по гипотенузе и острому углы ( их гипотенузы AB и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых AB и CD секущей AD), поэтому их площади равны. Следовательно, площади параллелограмма ABCD и прямоугольник HBCK также равны, т. е площадь прямоугольника HBSK равна S. По теореме о площади прямоугольника S=BC*BH, а так как BC=AD, то S=AD*BH.
Cлайд 9
Cлайд 10
Пусть S- площадь треугольника ABC. Примем сторону AB за основание треугольника и проведем высоту CH. Докажем, что S=0,5*AB*CH. Достроим треугольник ABC до параллелограмма ABCD. Треугольники ABC и DCB равны по трем сторонам (BC- общая сторона, AB=CD и AC=BD как противоположные стороны параллелограммаABCD), поэтому их площади равны. Следовательно, площадь S треугольника ABC равна половине площади параллелограмма ABCD, т.е. S=0,5*AB*CH.
Cлайд 11
Cлайд 12
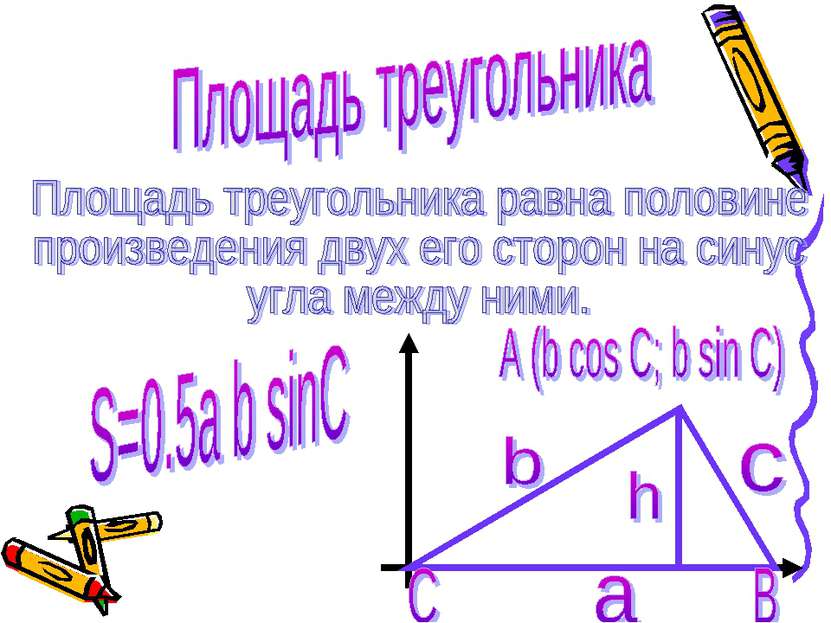
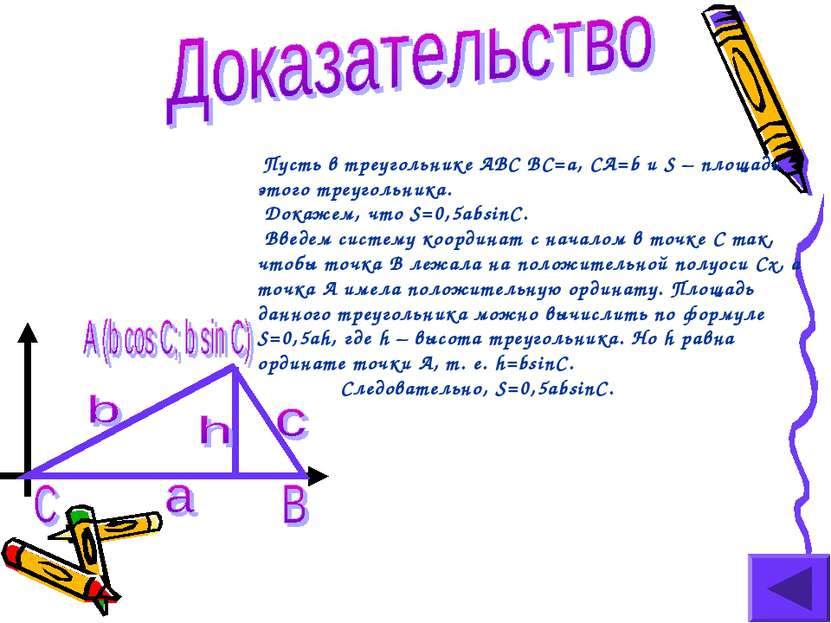
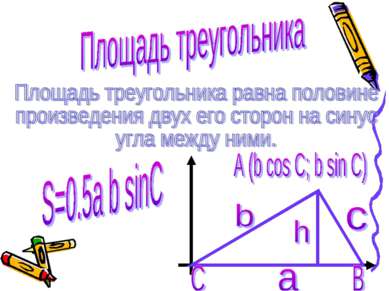
Пусть в треугольнике ABC BC=a, CA=b и S – площадь этого треугольника. Докажем, что S=0,5absinC. Введем систему координат с началом в точке С так, чтобы точка В лежала на положительной полуоси Сх, а точка А имела положительную ординату. Площадь данного треугольника можно вычислить по формуле S=0,5ah, где h – высота треугольника. Но h равна ординате точки А, т. е. h=bsinC. Следовательно, S=0,5absinC.
Cлайд 13
Cлайд 14
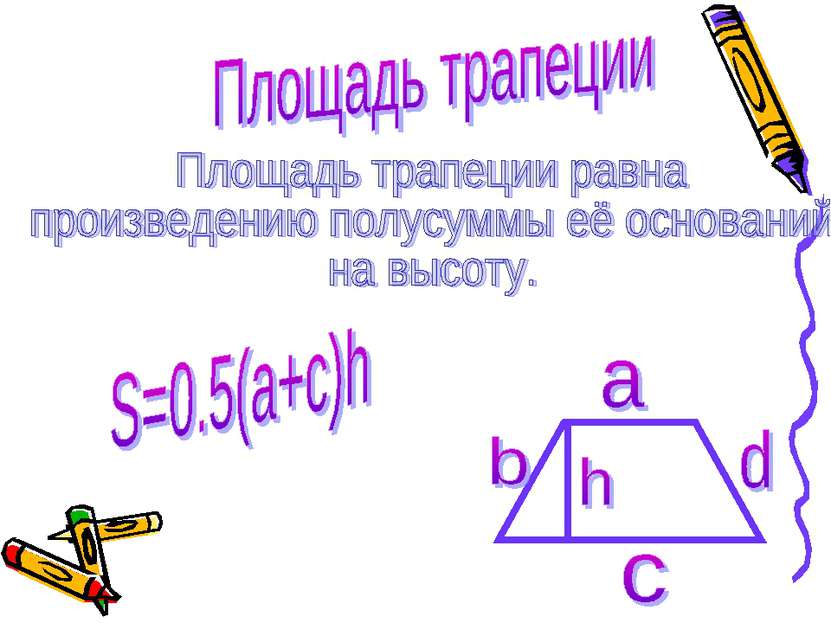
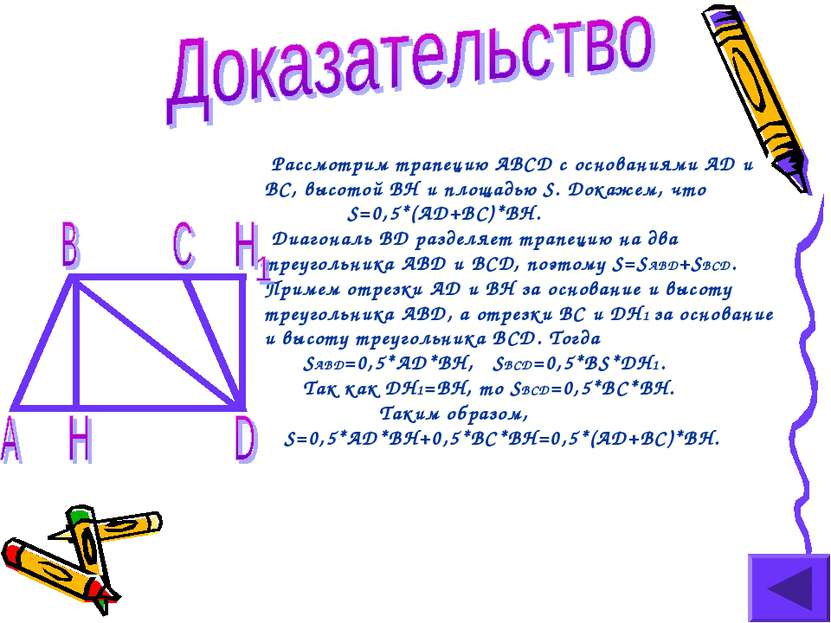
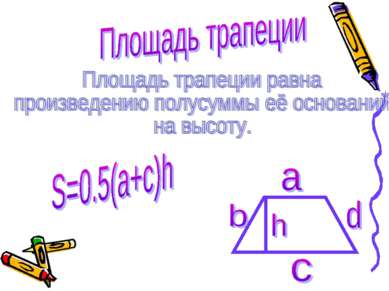
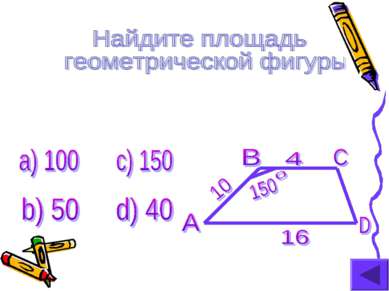
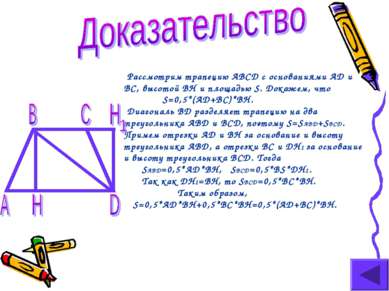Рассмотрим трапецию ABCD с основаниями AD и BC, высотой BH и площадью S. Докажем, что S=0,5*(AD+BC)*BH. Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S=SABD+SBCD. Примем отрезки AD и BH за основание и высоту треугольника ABD, а отрезки BC и DH1 за основание и высоту треугольника BCD. Тогда SABD=0,5*AD*BH, SBCD=0,5*BS*DH1. Так как DH1=BH, то SBCD=0,5*BC*BH. Таким образом, S=0,5*AD*BH+0,5*BC*BH=0,5*(AD+BC)*BH.
Cлайд 15
Cлайд 16
Cлайд 17
Cлайд 18
Cлайд 19
Cлайд 20
Cлайд 21
Cлайд 22
Cлайд 23
http://fio.ifmo.ru/archive/group13/c2wu5/text/test/tes9/test9.htm Геометрия, 7-9: Учеб. для общеобразоват. учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.- 14-е изд. – М.: Просвещение, 2004.- 384 с.: ил..
Cлайд 24
Cлайд 25
