X
Код презентации скопируйте его
C1 метод мажорант
Скачать эту презентацию
Презентация на тему C1 метод мажорант
Скачать эту презентациюCлайд 1
C1 метод мажорант
Cлайд 2
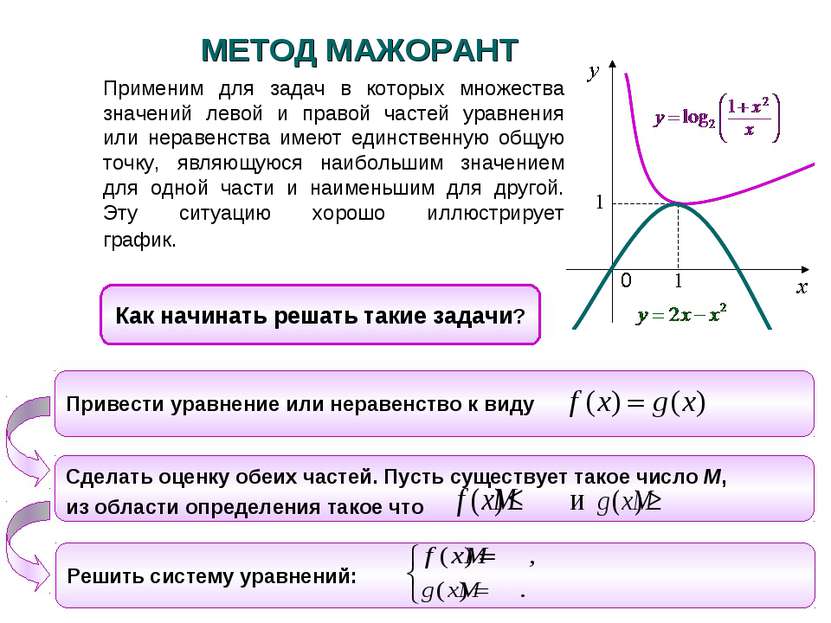
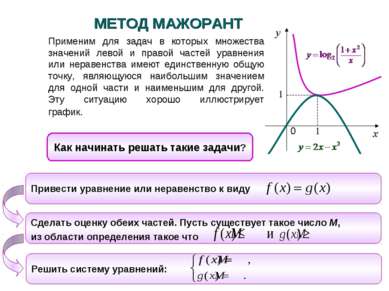Применим для задач в которых множества значений левой и правой частей уравнения или неравенства имеют единственную общую точку, являющуюся наибольшим значением для одной части и наименьшим для другой. Эту ситуацию хорошо иллюстрирует график. Как начинать решать такие задачи? МЕТОД МАЖОРАНТ Привести уравнение или неравенство к виду Сделать оценку обеих частей. Пусть существует такое число М, из области определения такое что
Cлайд 3
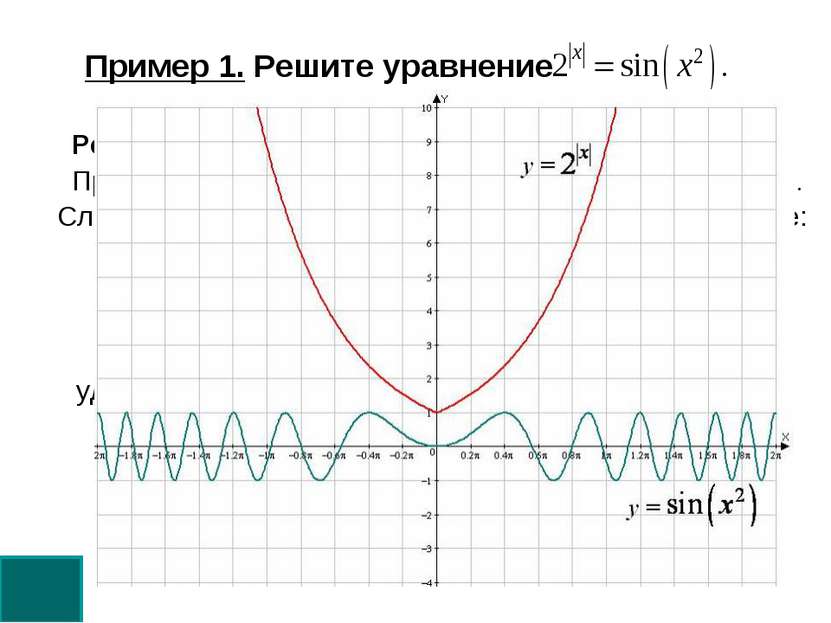
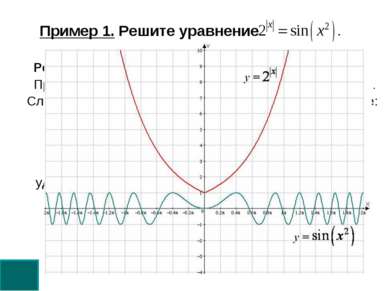удовлетворяет второму уравнению. Решение. Оценим обе части уравнения. При всех значениях х верны неравенства: Следовательно, данное уравнение равносильно системе:
Cлайд 4
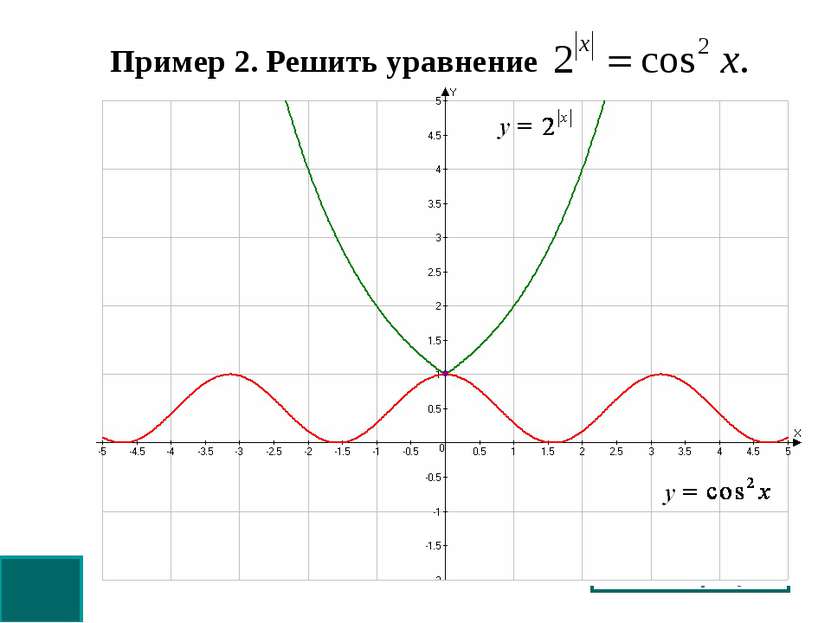
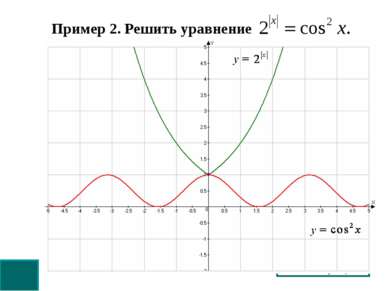Пример 2. Решить уравнение Решение: Оценим обе части уравнения. Следовательно, данное уравнение равносильно системе: При х = 0 второе уравнение обращается в тождество, значит х = 0 корень уравнения. Ответ: х = 0. Графическая иллюстрация
Cлайд 5
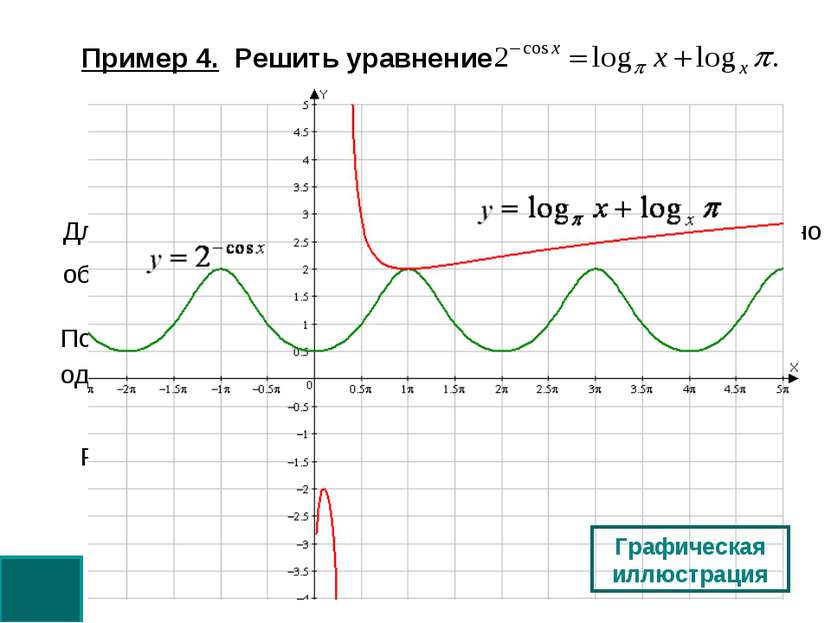
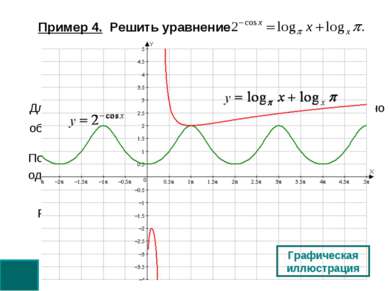Пример 4. Решить уравнение Для правой части (в силу неравенства для суммы двух взаимно обратных чисел) выполнено Поэтому уравнение имеет решения, если и только если одновременно выполнены два условия принимает значение от 0,5 до 2. Решение. Оценим обе части уравнения. Графическая иллюстрация
Cлайд 6
Пример 5. Решить уравнение Решением первого уравнения системы являются значения Решение. Оценим обе части уравнения.
Cлайд 7
Пример 6. Решить уравнение в том случае, когда оба слагаемых одновременно равны 1. Следовательно, данное уравнение равносильно системе уравнений . Решение.
Cлайд 8
Пример 7. Решить уравнение Решение. Очевидно, что почленно эти неравенства, получаем: Следовательно, левая часть равна правой, лишь при условии: Значит, данное уравнение равносильно системе уравнений: Решая систему уравнений, получаем корни: . Заметим, что перемножив Ответ:
Cлайд 9
Проверим справедливость первого равенства, подставив эти корни. При Пример 8. Решите уравнение Решение. Для решения уравнения оценим его части: Поэтому равенство возможно только при условии Сначала решим второе уравнение: Корни этого уравнения Итак, данное уравнение имеет единственный корень х = 0. Ответ: 0. При х = -1 имеем:
Cлайд 10
Пример 9. Найти все значения параметра а, при каждом из которых уравнение имеет решения. Найдите эти решения. При всех значениях х выражение При всех значения х выражения Поэтому Следовательно, левая часть уравнения не меньше 4, а правая часть – не больше 4. Получаем систему: Решение. Перепишем уравнение в виде
