X
Код презентации скопируйте его
Вероятность события 9 класс
Скачать эту презентацию
Презентация на тему Вероятность события 9 класс
Скачать эту презентациюCлайд 1
Вероятность события 9 класс
Cлайд 2
Встречаясь в жизни с различными событиями, мы часто даем оценку степени их достоверности. При этом произносим. Например, такие слова: «Это невероятно» - говорим мы о том, что вода в холодильнике закипела «Маловероятно, что сегодня будет идти дождь» - говорим, глядя на безоблачное небо летним утром
Cлайд 3
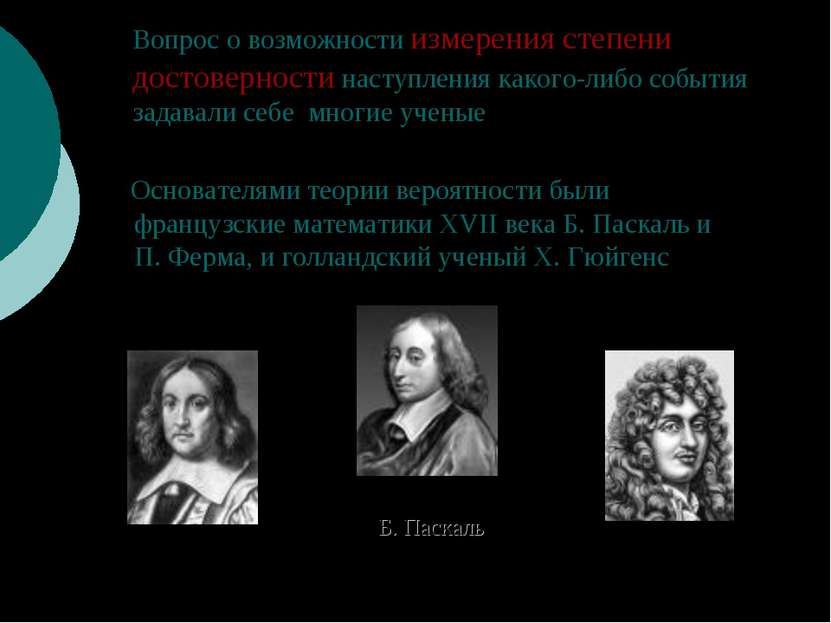
Вопрос о возможности измерения степени достоверности наступления какого-либо события задавали себе многие ученые Основателями теории вероятности были французские математики XVII века Б. Паскаль и П. Ферма, и голландский ученый Х. Гюйгенс Б. Паскаль П.Ферма Х. Гюйгенс
Cлайд 4
Наблюдая за игрой в кости, Б. Паскаль высказал идею измерения степени уверенности в выигрыше некоторым числом. Б. Паскаль рассуждал, что , когда игрок бросает игральную кость, он не знает, какое число очков выпадет. Но он знает, что каждое из чисел - 1, 2, 3, 4, 5, 6 имеет одинаковую долю успеха в своем появлении. Появление же одного из этих чисел в каждом испытании – событие достоверное
Cлайд 5
Вероятность события Если принять возможность наступления достоверного события за 1, то возможность появления, например, шестерки в шесть раз меньше, т. е. равна 1/6 Долю успеха того или иного события математики называют вероятностью этого события (от латинского probabilitas – «вероятность»)
Cлайд 6
Вероятность события Если буквой А обозначить событие – «выпало 6 очков» при одном бросании игральной кости, то вероятность события А обозначают Р(А) и записывают Р(А) = 1/6 Читают: «вероятность события А равна одной шестой»
Cлайд 7
Задача Поверхность рулетки разделена диаметрами на 4 части. Найти вероятность того, что раскрученная стрелка рулетки остановится в секторе 3 4 3 1 2 В одном испытании с раскручиванием стрелки возможны 4 равновозможных события (исхода испытания). Достоверное событие – «стрелка остановится на каком-нибудь из секторов». Вероятность наступления достоверного события равна 1, а вероятность события А – «стрелка остановится в секторе 3» в 4 раза меньше, т. е. равна 1/4 Р(А) = 1/4
Cлайд 8
Вероятность события Помимо рассмотренных элементарных событий можно рассматривать и более сложные события. Например, «выпадение четного числа очков при одном бросании игральной кости» Это событие наступает в трех случаях – когда выпадет 2, или 4, или 6 очков. Все эти исходы благоприятствуют событию А, тогда Р(А) = 3/6 = 1/2
Cлайд 9
Вероятность события Если в некотором испытании существует n равновозможных попарно несовместных исхода и m из них благоприятствуют событию А, то вероятностью наступления события А называют отношение m / n Р(А) = m / n
Cлайд 10
Задача Найти вероятность появления при одном бросании кости числа очков, большего 4 Событию А – «появление числа очков, большего 4», благоприятствуют 2 исхода (появление 5 или 6 очков), т. е. m = 2, n = 6, следовательно, Р(А) = m / n = 2/6 = 1/3
Cлайд 11
Задача Поверхность рулетки разделена На 8 равных частей. Найти вероятность того, что после раскручивания стрелка рулетки остановится на закрашенной части 4 3 1 2 Существует 8 исходов испытания, т. е. n = 8 В закрашенную часть рулетки попадают три сектора, значит число благоприятствующих исходов m = 3 5 6 7 8 Р(А) = m / n = 3/8
Cлайд 12
Если событие А - достоверное, то ему благоприятствуют все возможные исходы испытания, т. e. m = n , тогда Р(А) = m/n = 1 О вероятностях наступления достоверных, невозможных и случайных событий на основании формулы Р(А) = m/n можно рассуждать следующим образом Если событие А – невозможное, то не существует исходов благоприятствующих его появлению т. e. m = 0 , тогда Р(А) = m/n = 0/n = 0 Если событие А – случайное, то число m благоприятствующих его появлению исходов удовлетворяет условию 0 < m < n , тогда 0 < Р(А) = m/n < 1 0 ≤ P(A) ≤ 1
Cлайд 13
Задача Перечислите все элементарные возможные события, которые могут произойти в результате: а) подбрасывания монеты б) подбрасывания тетраэдра с гранями, занумерованными числами 1, 2, 3, 4 (появление орла, появление решки) (грань 1, или 2, или 3, или 4) 1 2 4
Cлайд 14
Задача В ящике находятся 2 белых и 3 черных шара. Наугад вынимается один шар. Какова вероятность того, что вынутый шар а) белый б) черный Существует 5 равновозможных исходов испытания, n = 5 a) число благоприятствующих исходов m = 2 Р(А) = m / n = 2/5 б) число благоприятствующих исходов m = 3 Р(А) = m / n = 3/5
