X
Код презентации скопируйте его
Мастер -класс "Использование презентаций Power Point на урока математики при построении графиков функции"
Скачать эту презентацию
Презентация на тему Мастер -класс "Использование презентаций Power Point на урока математики при построении графиков функции"
Скачать эту презентациюCлайд 1
Мастер-класс «Использование презентаций PowerPoint на уроках математики при построении графиков функции» Бурганиева Альфия Рафисовна, учитель математики высшей квалификационной категории Кучуковской средней общеобразовательной щколы Агрызского муниципального района РТ, Бурганиев Ринат Габдрахманович, учитель математики и физики первой квалификационной категории Кичкетанской средней общеобразовательной школыАгрызского муниципального района РТ
Cлайд 2
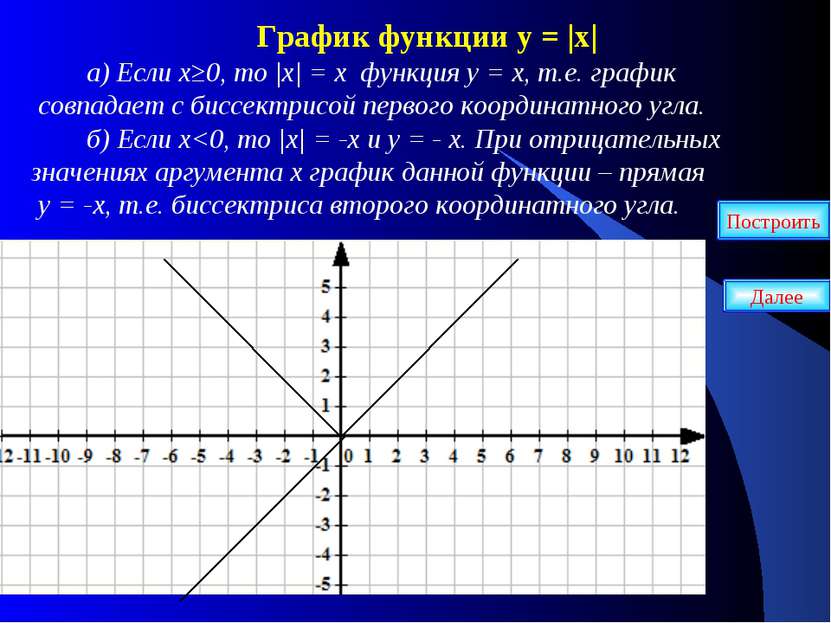
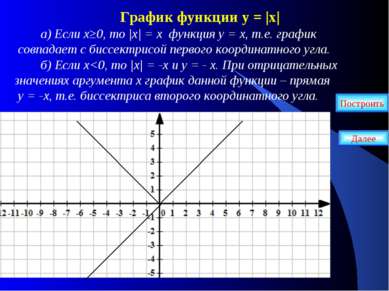График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х
Cлайд 3
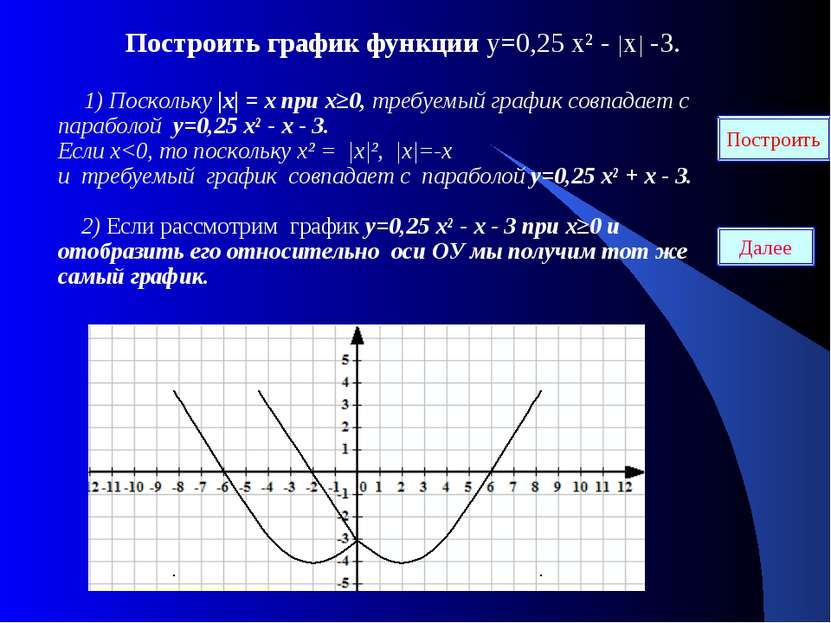
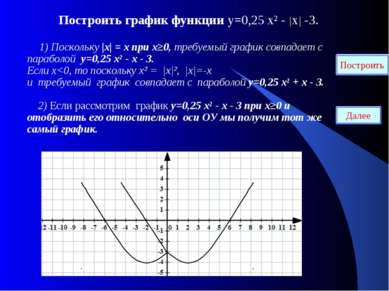Построить график функции у=0,25 х² - |х| -3. 1) Поскольку |х| = х при х≥0, требуемый график совпадает с параболой у=0,25 х² - х - 3. Если х
Cлайд 4
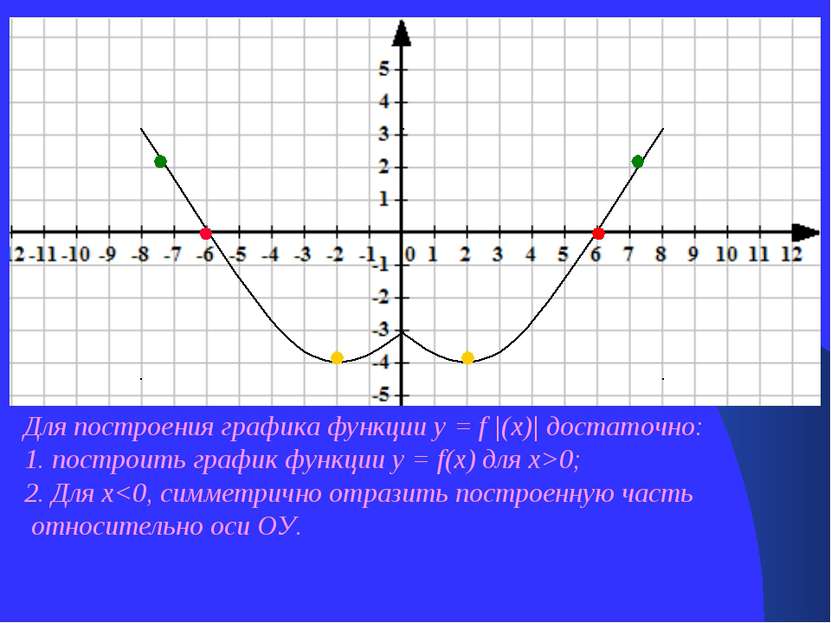
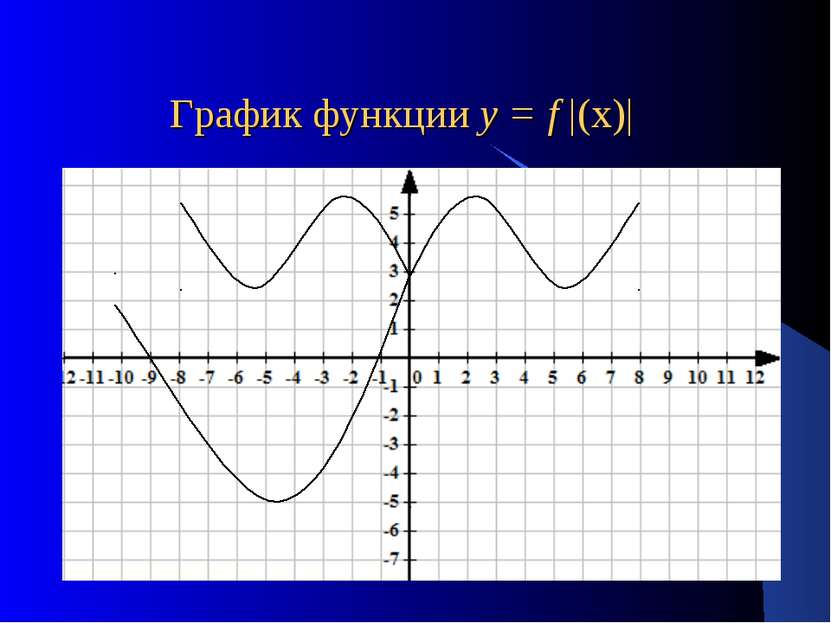
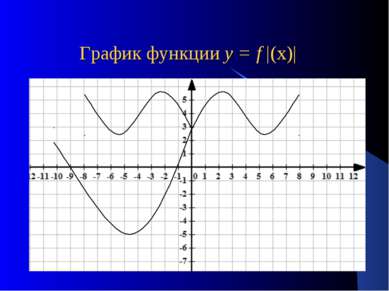
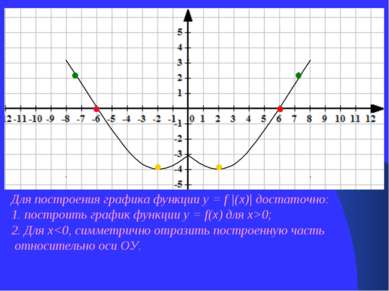Для построения графика функции у = f |(х)| достаточно: 1. построить график функции у = f(х) для х>0; 2. Для х
Cлайд 5
График функции у = f |(х)|
Cлайд 6
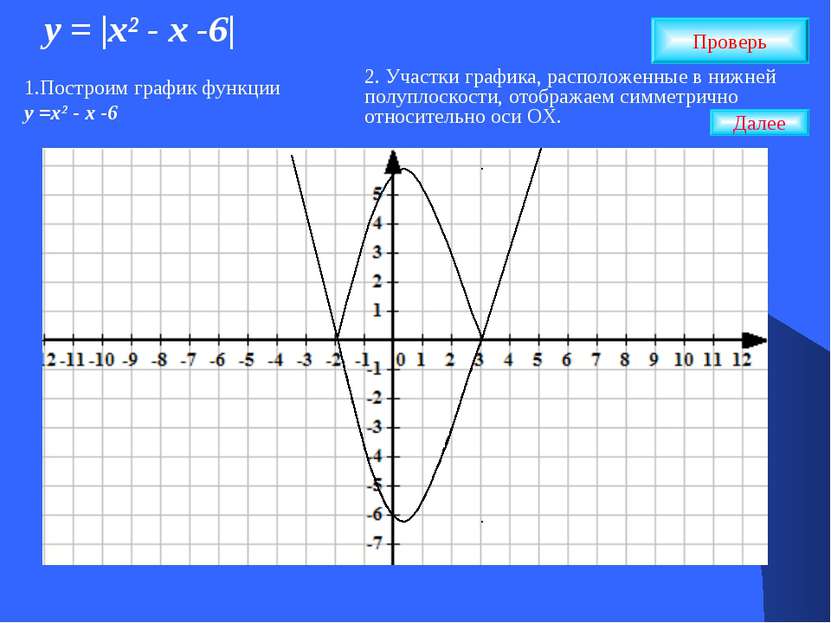
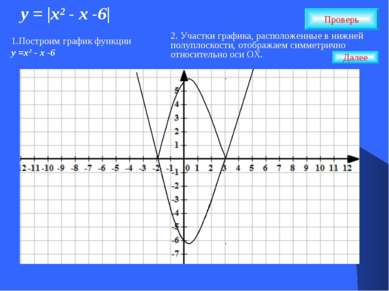у = |х² - х -6| Проверь 1.Построим график функции у =х² - х -6 2. Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. Далее
Cлайд 7
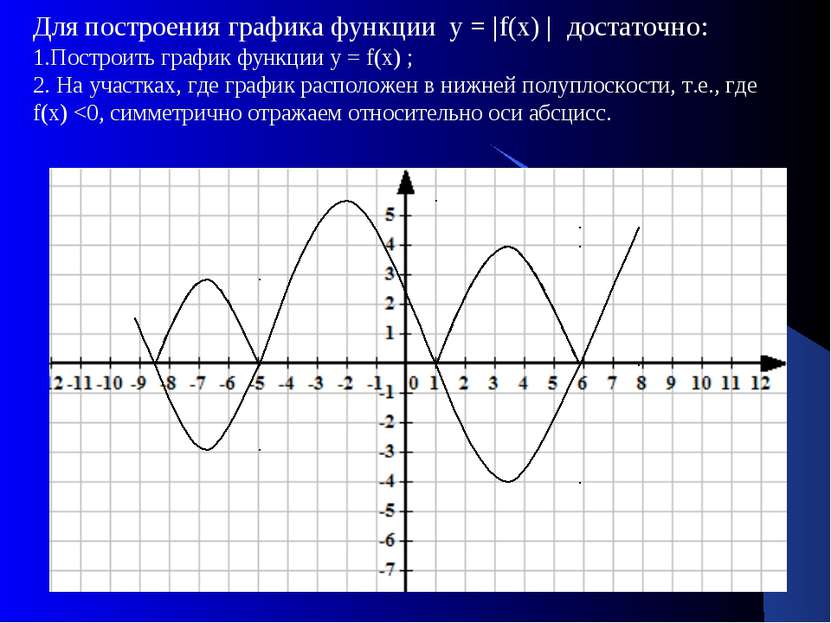
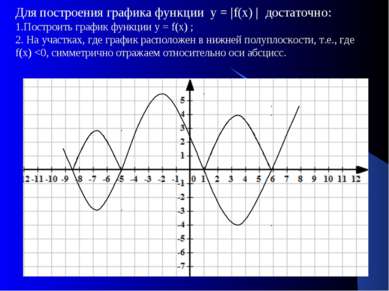Для построения графика функции у = |f(х) | достаточно: 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х)
Cлайд 8
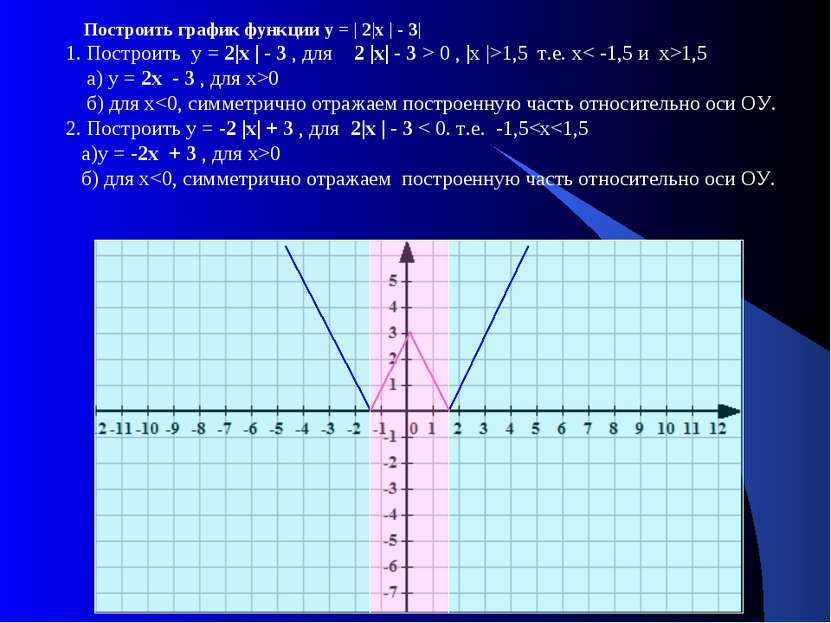
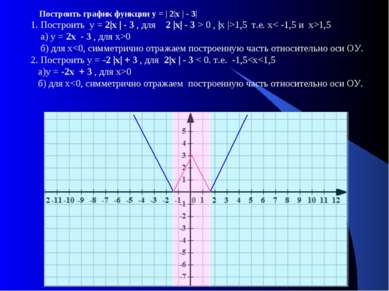Построить график функции у = | 2|х | - 3| 1. Построить у = 2|х | - 3 , для 2 |х| - 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5 а) у = 2х - 3 , для х>0 б) для х
Cлайд 9
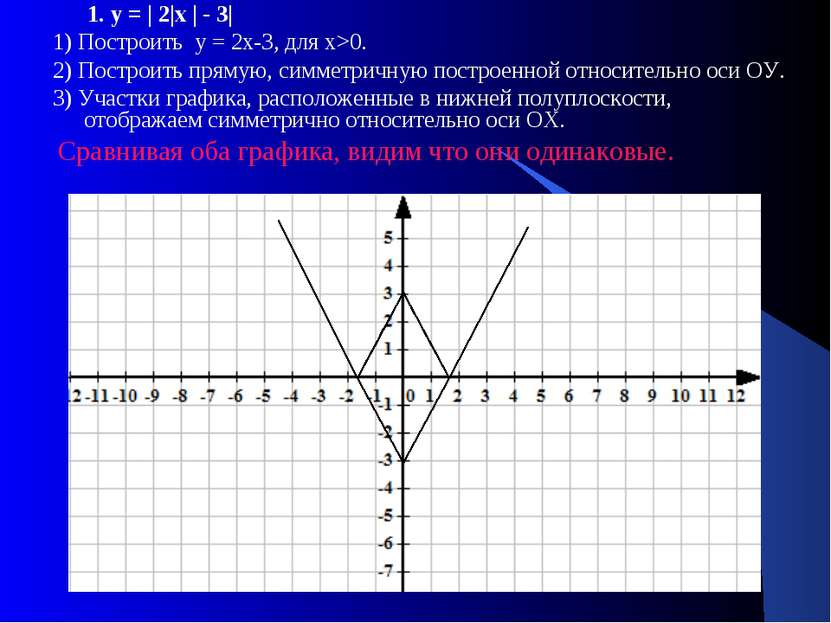
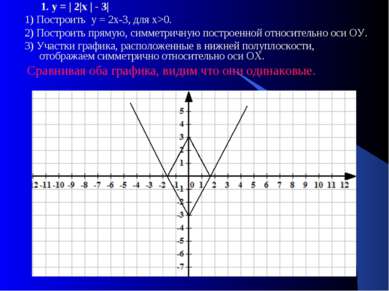1. у = | 2|х | - 3| 1) Построить у = 2х-3, для х>0. 2) Построить прямую, симметричную построенной относительно оси ОУ. 3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Cлайд 10
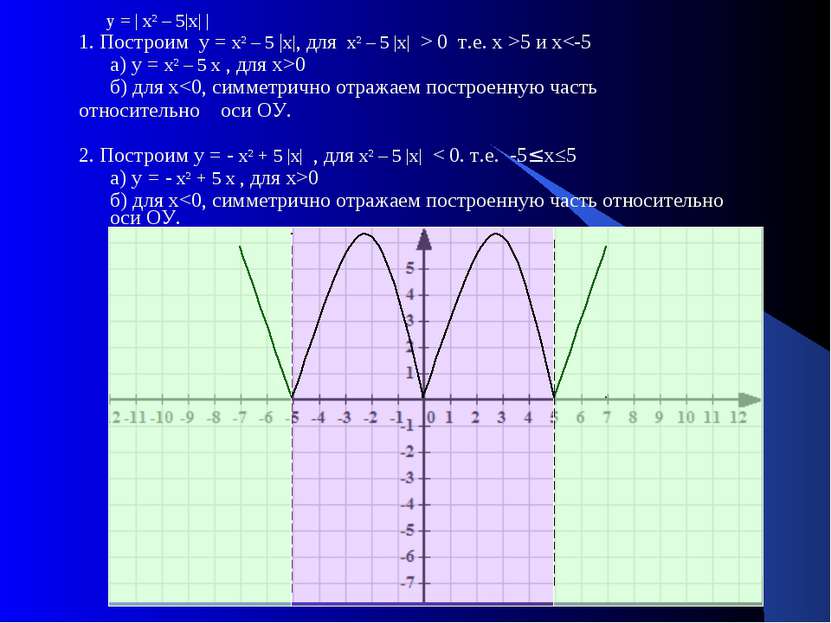
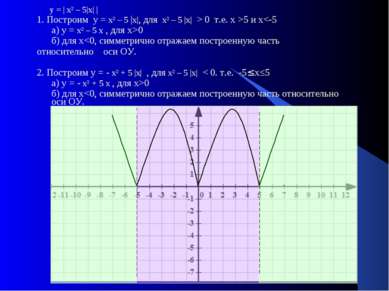у = | х² – 5|х| | 1. Построим у = х² – 5 |х|, для х² – 5 |х| > 0 т.е. х >5 и х0 б) для х0 б) для х
Cлайд 11
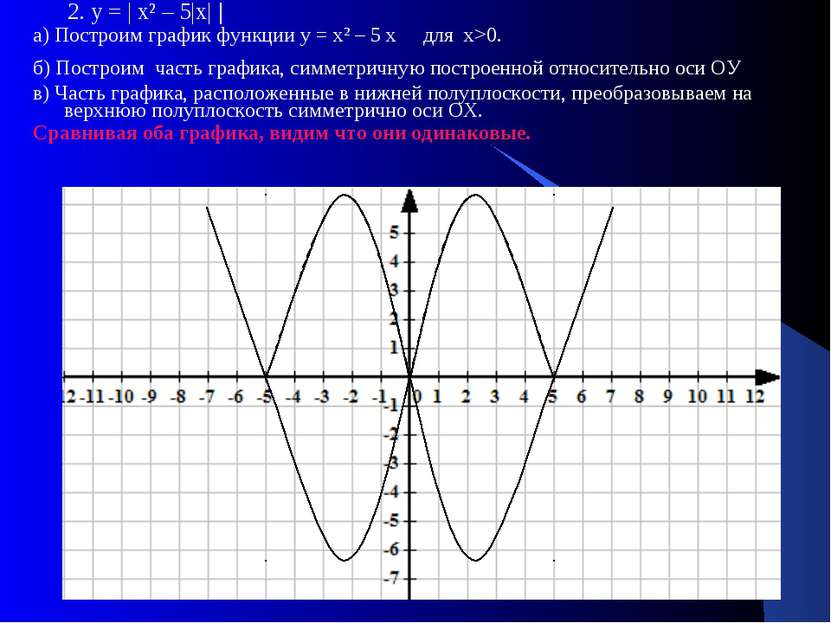
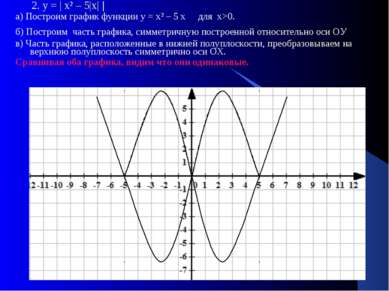2. у = | х² – 5|х| | а) Построим график функции у = х² – 5 х для х>0. б) Построим часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Cлайд 12
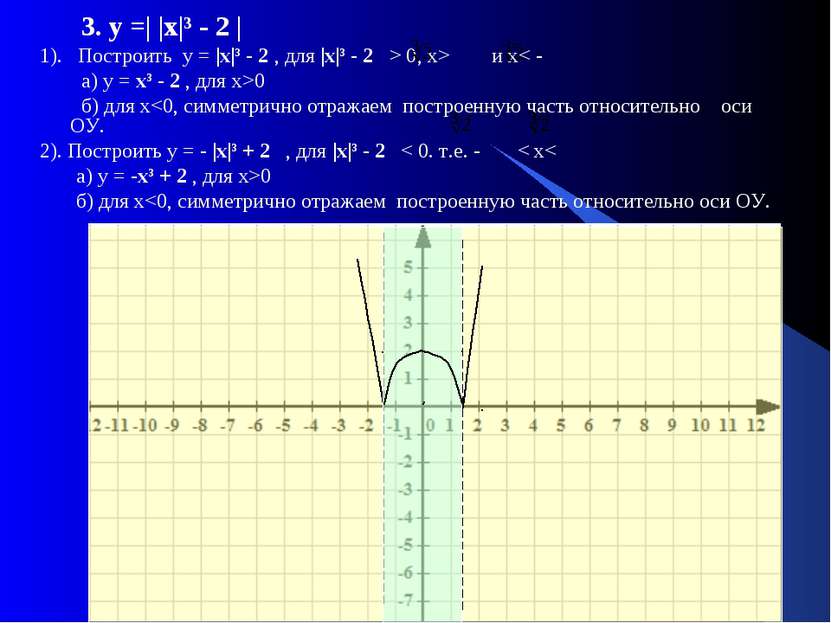
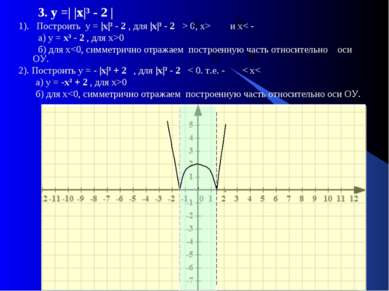3. у =| |х|³ - 2 | 1). Построить у = |х|³ - 2 , для |х|³ - 2 > 0, x> и x< - а) у = х³ - 2 , для х>0 б) для х0 б) для х
Cлайд 13
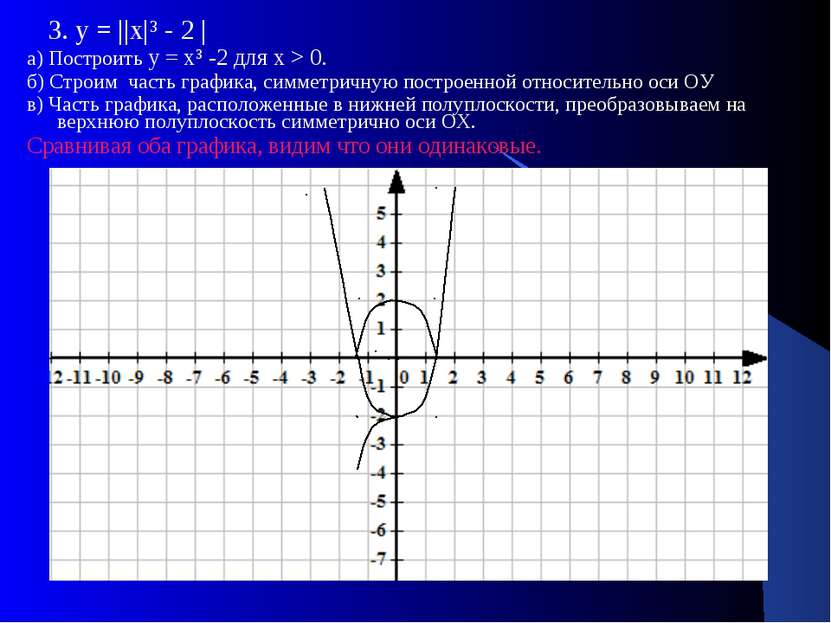
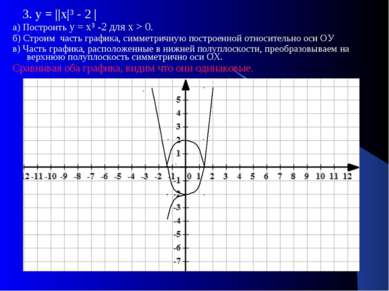3. у = ||х|³ - 2 | а) Построить у = х³ -2 для х > 0. б) Строим часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Cлайд 14
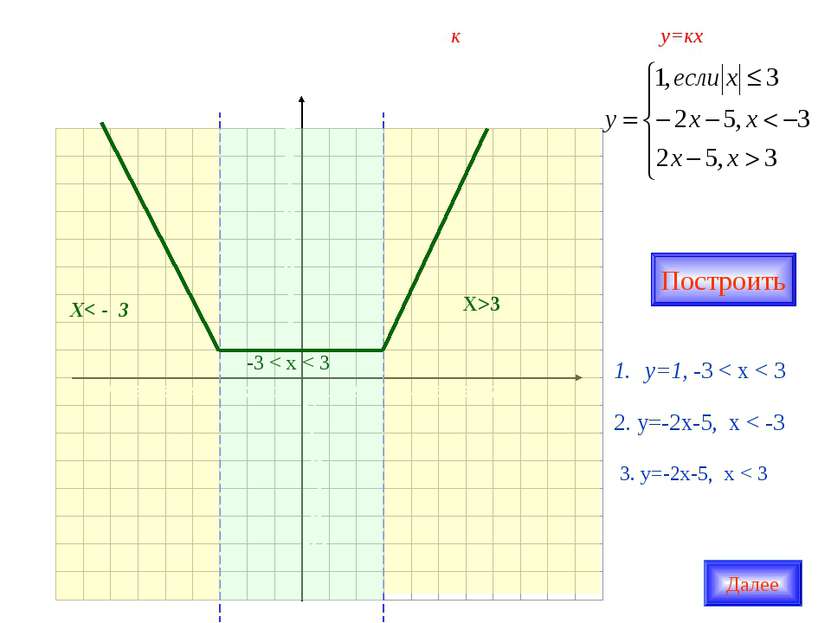
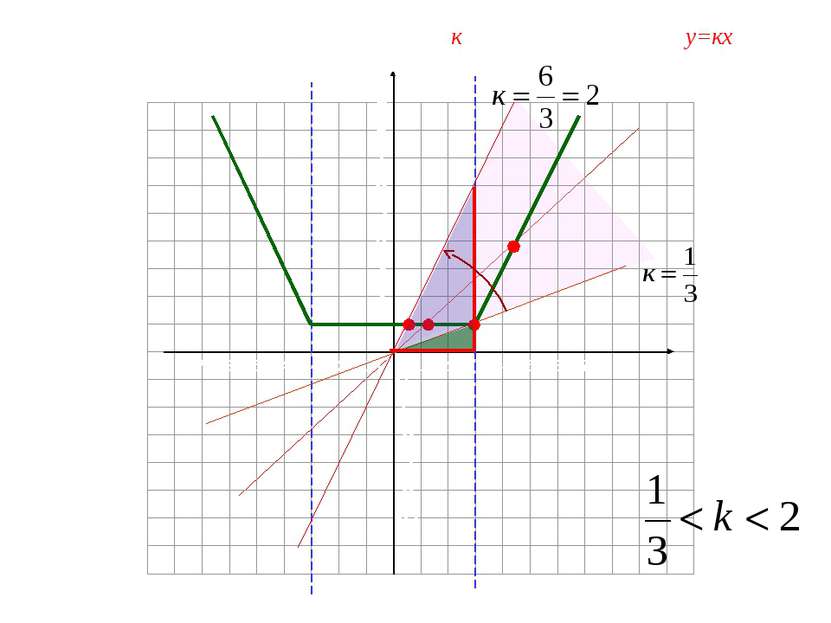
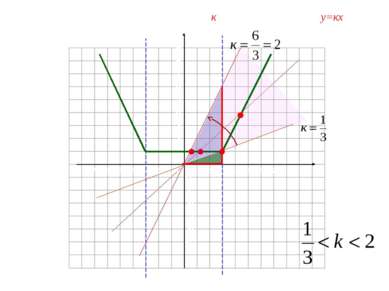
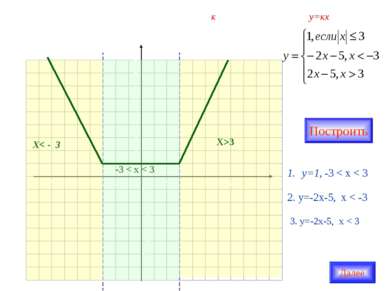Найдите все положительные значения к, при которых прямая у=кх пересекает в двух точках ломанную, заданную условиями: Х>3 Х< - 3 -3 < x < 3 Построить у=1, -3 < x < 3 2. у=-2х-5, x < -3 3. у=-2х-5, x < 3 Далее
Cлайд 15
Найдите все положительные значения к, при которых прямая у=кх пересекает ломанную в двух точках.
Cлайд 16
-1 -2 -3 -4 -5 -6 1 2 3 4 5 6 7 1. у = IхI 2. у = Iх+1I Ответ: (-1;4), (-4;-1), (4;1). Построить о -7 -6 -5 -4 -3 -2 -1 9 8 7 6 5 4 3 2 1 у х 2. у = Iх+1I – 4 Решить систему уравнений Далее
