X
Код презентации скопируйте его
Математические методы оценки взаимосвязи
Скачать эту презентациюПрезентация на тему Математические методы оценки взаимосвязи
Скачать эту презентациюCлайд 2
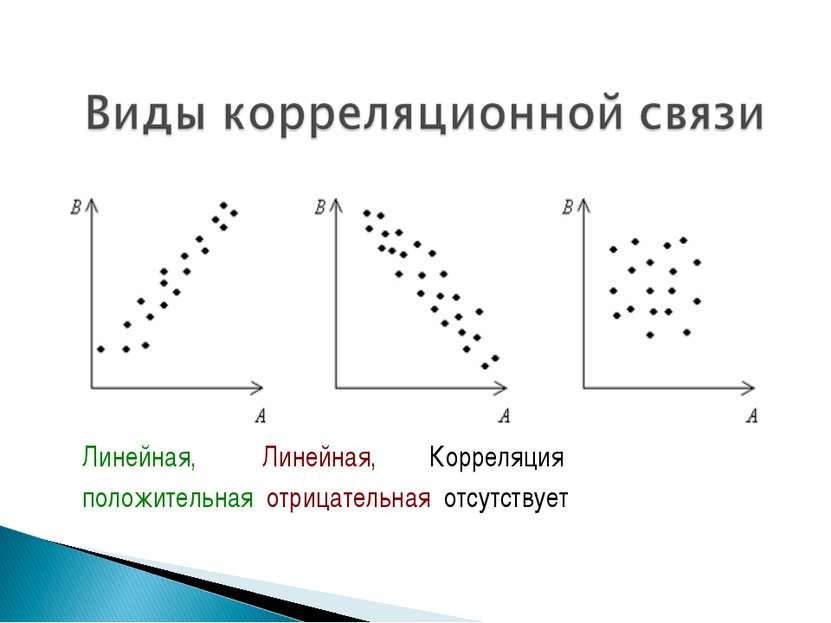
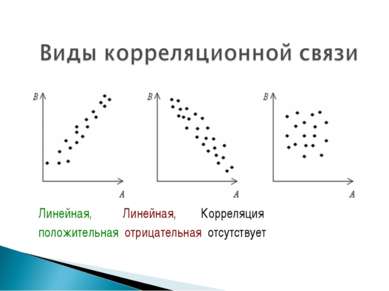
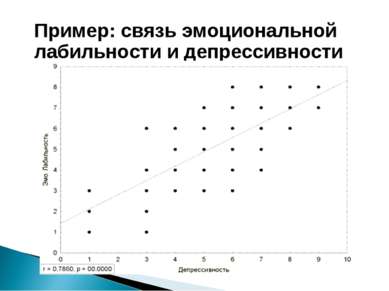
 Корреляционная связь - это согласованное изменение двух признаков, отражающее, что изменчивость одного признака находится в соответствии с изменчивостью другого «Когда изменяется X, то Y тоже меняется» Не путать с причинно-следственной связью!
Корреляционная связь - это согласованное изменение двух признаков, отражающее, что изменчивость одного признака находится в соответствии с изменчивостью другого «Когда изменяется X, то Y тоже меняется» Не путать с причинно-следственной связью!
Cлайд 4
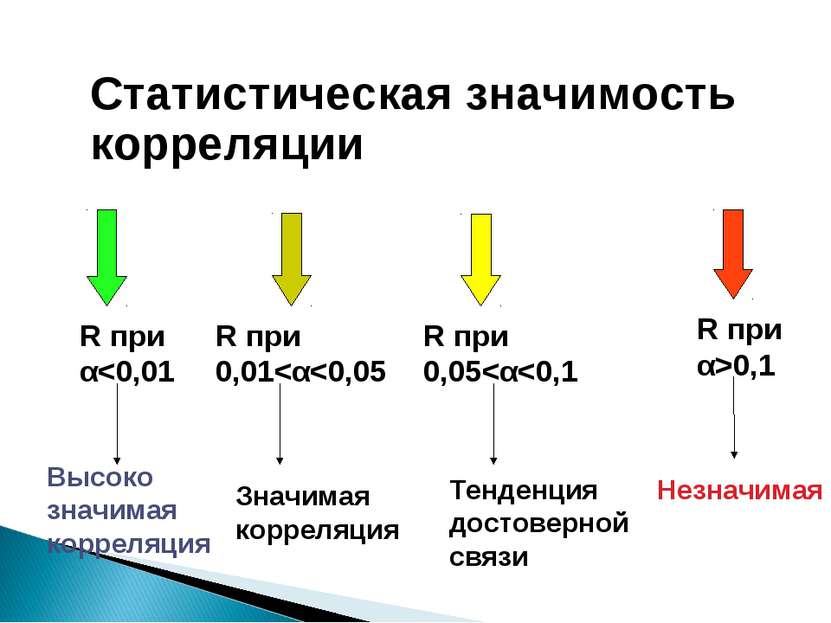
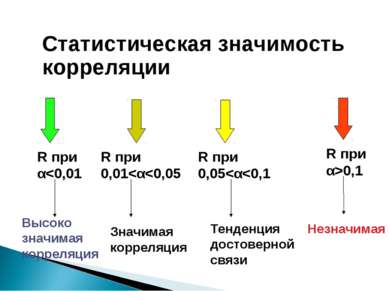
 Сила корреляционной связи Выражается через значение коэффициента корреляции (R) Бывает: R(а,b)>0,70 - сильная связь между a и b 0,5
Сила корреляционной связи Выражается через значение коэффициента корреляции (R) Бывает: R(а,b)>0,70 - сильная связь между a и b 0,5
Cлайд 7
 для параметрических шкал - коэффициент Rx,y Пирсона для данных ранговой и параметрических шкал - Rs Спирмена для данных ранговых шкал — τ (тау) критерий Кендалла для дихотомических шкал - φ коэффициент ассоциации Пирсона
для параметрических шкал - коэффициент Rx,y Пирсона для данных ранговой и параметрических шкал - Rs Спирмена для данных ранговых шкал — τ (тау) критерий Кендалла для дихотомических шкал - φ коэффициент ассоциации Пирсона
Cлайд 8
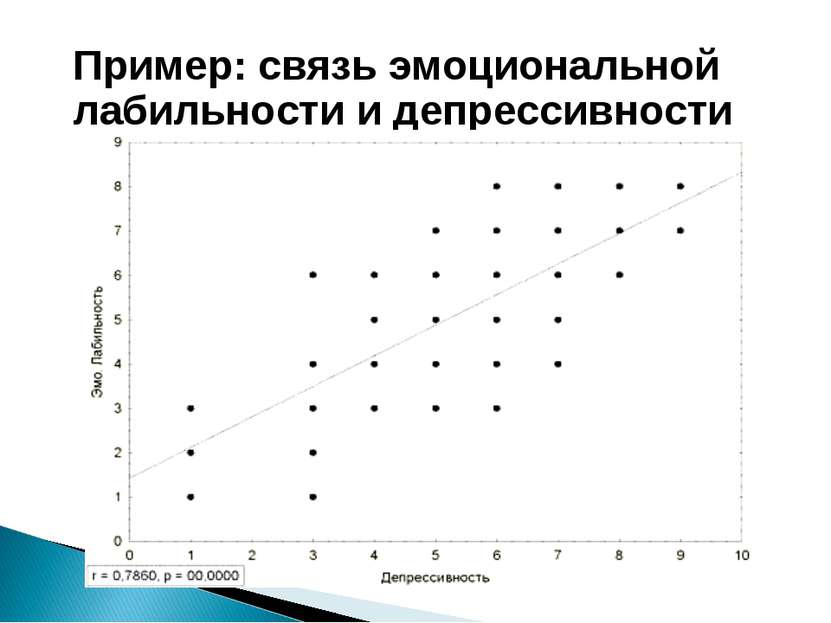
 где xi и yi — показатели под номером i, X и Y — средние Ограничения: параметрические данные; нормальное распределение в обеих выборках; 5>nx,ny>5000; nx=ny Возможности: определяет силу и направление корреляционной связи между двумя признаками (измеренными в одной и той же группе или между двумя рядами значений, полученных в двух группах)
где xi и yi — показатели под номером i, X и Y — средние Ограничения: параметрические данные; нормальное распределение в обеих выборках; 5>nx,ny>5000; nx=ny Возможности: определяет силу и направление корреляционной связи между двумя признаками (измеренными в одной и той же группе или между двумя рядами значений, полученных в двух группах)
Cлайд 9
 n – количество пар рангов, d – разность между рангами по X и по Y Возможности: измеряет силу и направление корреляционной связи; работает со всеми количественными данными; непараметрический. Ограничения: 5< n< 40 (таблицы); при увеличении n становится менее мощным; требует поправок для связанных рангов
n – количество пар рангов, d – разность между рангами по X и по Y Возможности: измеряет силу и направление корреляционной связи; работает со всеми количественными данными; непараметрический. Ограничения: 5< n< 40 (таблицы); при увеличении n становится менее мощным; требует поправок для связанных рангов
Cлайд 10
 1. В таблице 1,2 столбцы заполнить значениями X и Y 2. В столбце 3 присвоить ранги значениям X по Правилам ранжирования. Аналогично для значений Y (в столбце 4) 3. Разности между каждой парой рангов (по строчка) занести в 5-й столбец как d 4. Возвести каждую разность в квадрат, записать в 6-й столбец как d2 5. Посчитать сумму всех d2, записать ее как ∑(d2)=
1. В таблице 1,2 столбцы заполнить значениями X и Y 2. В столбце 3 присвоить ранги значениям X по Правилам ранжирования. Аналогично для значений Y (в столбце 4) 3. Разности между каждой парой рангов (по строчка) занести в 5-й столбец как d 4. Возвести каждую разность в квадрат, записать в 6-й столбец как d2 5. Посчитать сумму всех d2, записать ее как ∑(d2)=
Cлайд 11
 6. Считать значение коэффициента: 7. При наличии связанных рангов в числитель дроби сделать поправки +Tx и +Ty: где ax и by — объем каждой группы одинаковых рангов в соответствующем ранговом ряду
6. Считать значение коэффициента: 7. При наличии связанных рангов в числитель дроби сделать поправки +Tx и +Ty: где ax и by — объем каждой группы одинаковых рангов в соответствующем ранговом ряду