X
Код презентации скопируйте его
Статистические показатели
Скачать эту презентацию
Презентация на тему Статистические показатели
Скачать эту презентациюCлайд 1
СТАТИСТИКА I (теория статистики) Часть 4. Статистические показатели. Кафедра Маркетинга и менеджмента (ММ) Бесплатные презентации http://prezentacija.biz/
Cлайд 2
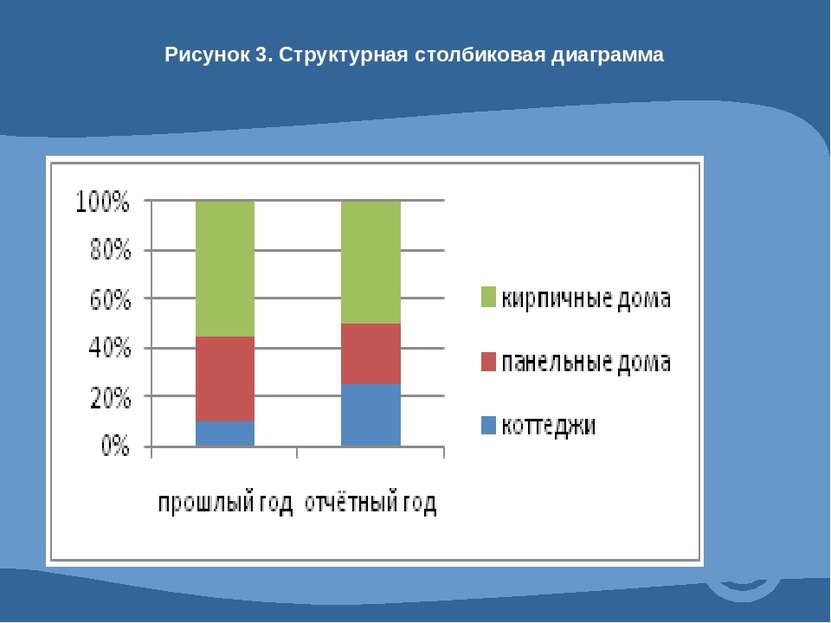
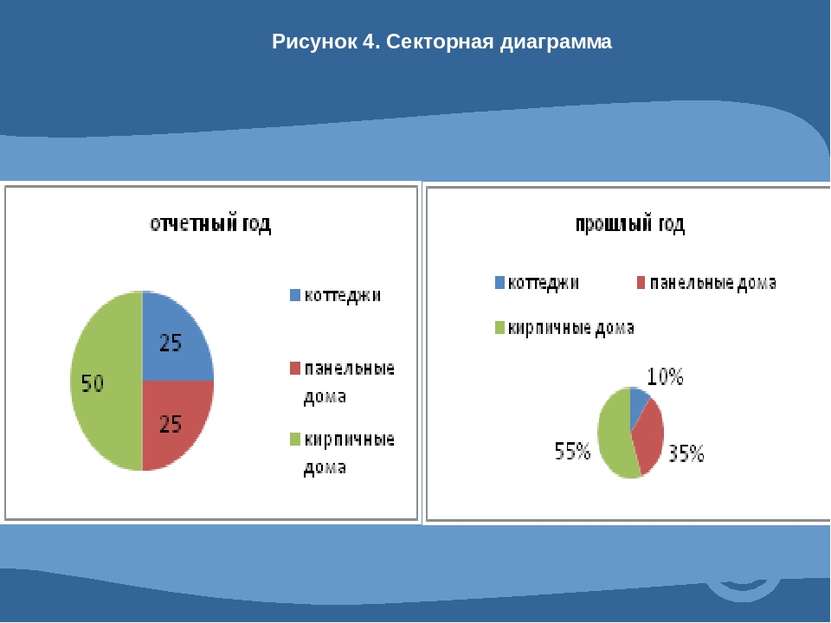
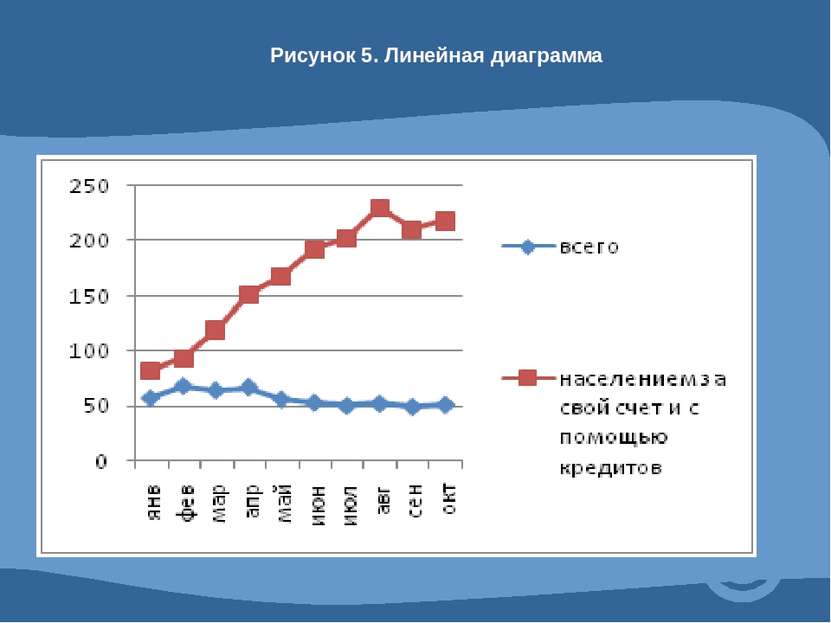
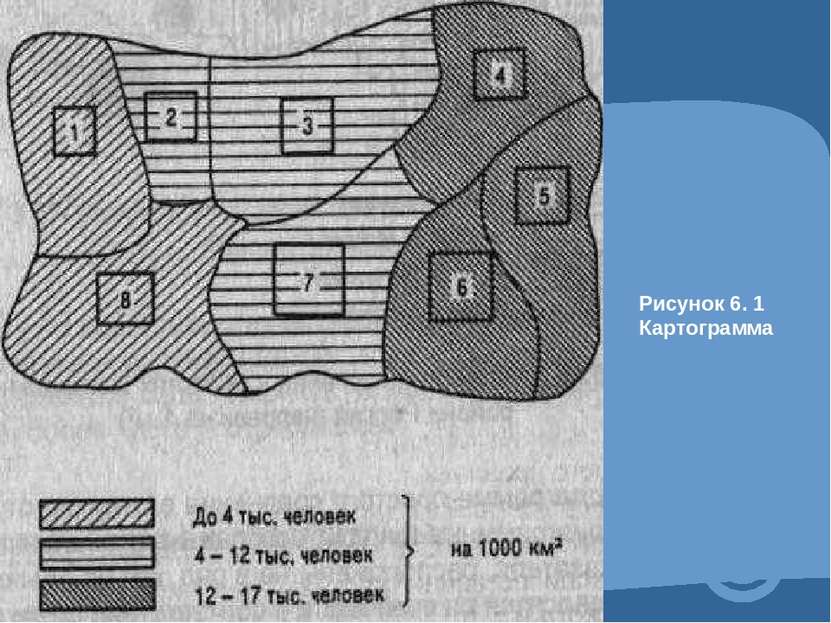
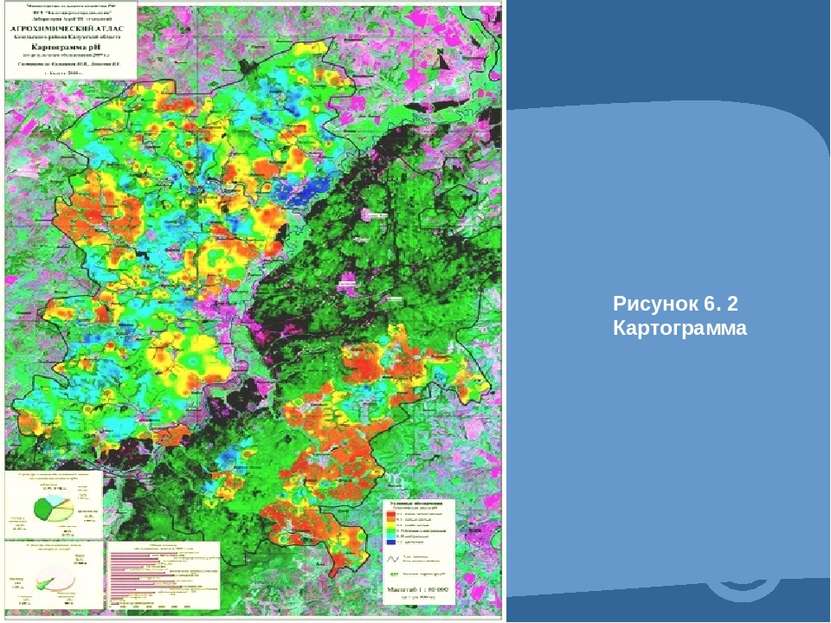
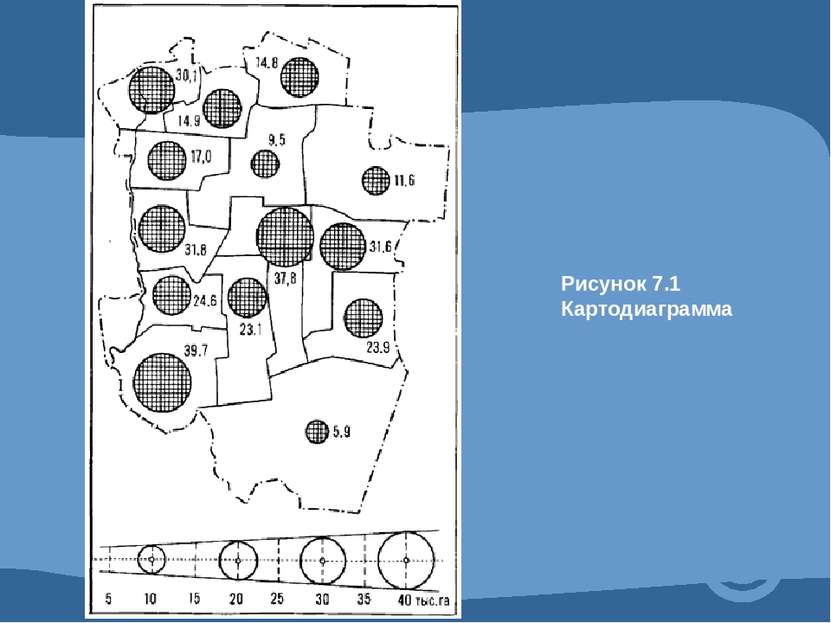
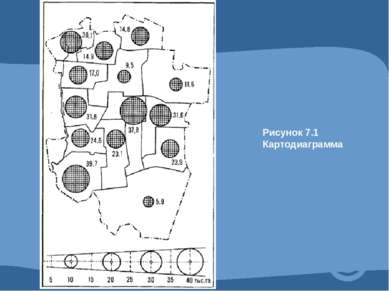
4.1 Абсолютные и относительные показатели. Абсолютные показатели характеризуют итоговую численность единиц совокупности или ее частей, размеры (объемы, уровни) изучаемых явлений и процессов, выражают временные характеристики. Относительные показатели - это цифровые обобщающие показатели, они есть результат сопоставления двух статистических величин.
Cлайд 3
Cлайд 4
Cлайд 5
Cлайд 6
Cлайд 7
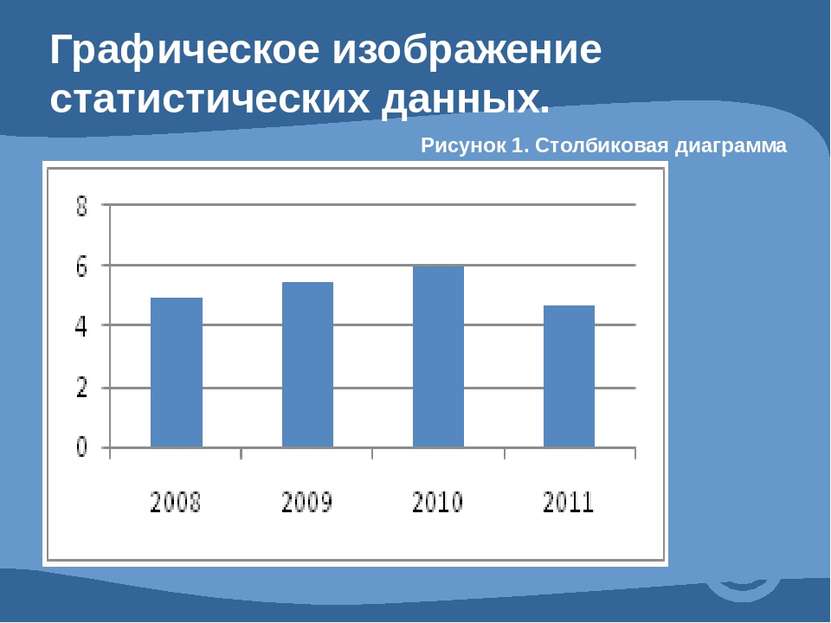
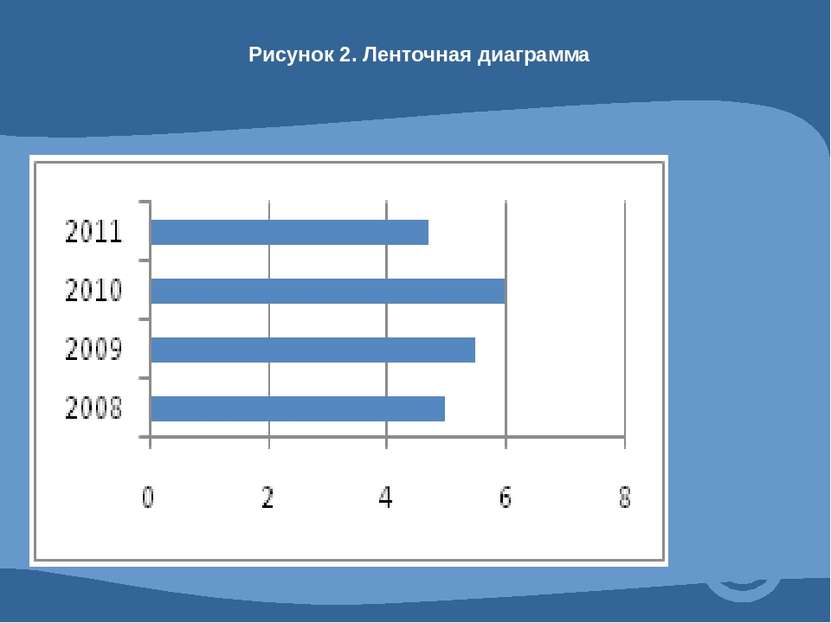
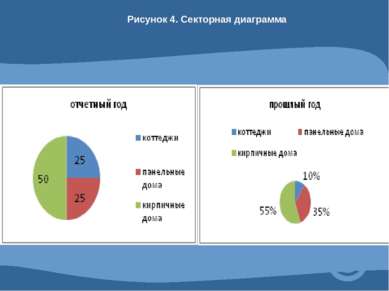
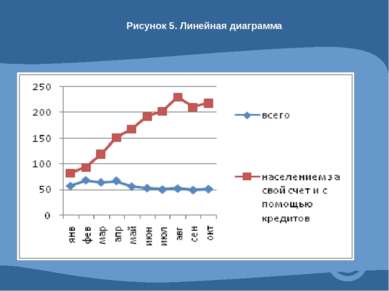
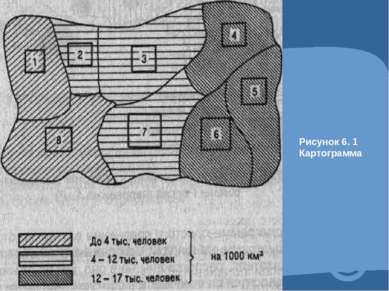
4.2 Средние величины и их графические изображения. Средней величиной называют показатель, который характеризует обобщен- ное значение признака или группы признаков в исследуемой совокупности.
Cлайд 8
Виды средних: Взвешенными средними называют величины, которые учитывают, что некоторые варианты значений признака могут иметь различную численность, в связи с чем каждый вариант приходится умножать на эту численность. Иными словами, «весами» выступают числа единиц совокупности в разных группах, т.е. каждый вариант «взвешивают» по своей частоте. Частоту f называют статистическим весом или весом средней. Разновидностью простой средней арифметической служит средняя хронологическая величина, когда имеются моментные статистические величины на определенную одинаковую дату, например, на 1-е число каждого месяца в году.
Cлайд 9
В статистике соблюдаются следующие принципы применения сред них величин. 1. Необходим обоснованный выбор статистической совокупности, для которой определяется средняя величина. 2. При определении средней величины исходят из качественного содержания статистических величин, учитывая возможную взаимосвязь изучаемых признаков. 3. Средняя величина должна рассчитываться по однородной сово купности, которая позволяет применять метод группировки, предпола гающий расчет системы обобщающих показателей. 4. Общая средняя величина должна подкрепляться и поясняться групповыми средними величинами.
Cлайд 10
Средняя арифметическая - самый распространенный вид средней. Она используется, когда расчет осуществляется по не сгруппированным статистическим данным, где нужно получить среднее слагаемое. Средняя арифметическая - это такое среднее значение признака, при получении которого сохраняется неизменным общий объем признака в совокупности. Формула средней арифметической (простой) имеет вид - средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений; n - численность совокупности; хi- величины, для которых исчисляется средняя. Формула средней арифметической (взвешенной) имеет вид - частота (повторяемость индивидуальных значений признака). При расчете средних величин отдельные значения признака, который осредняется, могут повторяться, поэтому расчет средней величины производится по сгруппированным данным. Средняя арифметическая взвешенная - При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам.
Cлайд 11
Средняя гармоническая. Эту среднюю называют обратной средней арифметической. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. В статистической практике чаще используется гармоническая взвешенная, формула которой имеет вид Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. Средняя гармоническая простая - Средние гармонические используются тогда, когда по экономическому содержанию имеется информация для числителя, а для знаменателя ее необходимо предварительно определить. Средняя гармоническая взвешенная - используется для расчета средних показателей не только в статике, но и в динамике, когда известны индивидуальные значения признака и веса W за ряд временных интервалов.
Cлайд 12
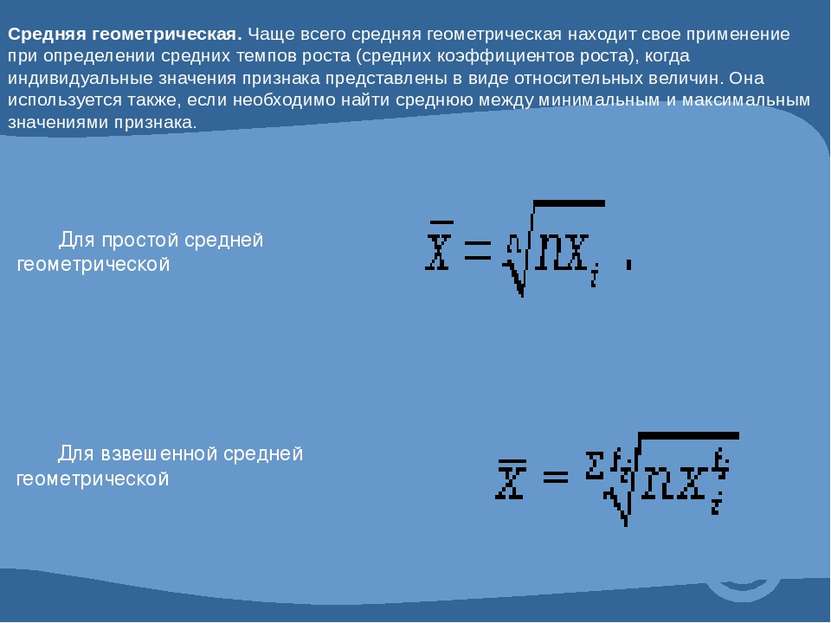
Средняя геометрическая. Чаще всего средняя геометрическая находит свое применение при определении средних темпов роста (средних коэффициентов роста), когда индивидуальные значения признака представлены в виде относительных величин. Она используется также, если необходимо найти среднюю между минимальным и максимальным значениями признака. Для простой средней геометрической Для взвешенной средней геометрической Средняя геометрическая простая - Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста.
Cлайд 13
Средняя квадратическая величина. Основной сферой ее применения является измерение вариации признака в совокупности (расчет среднего квадратического отклонения). Формула простой средней квадратической Формула взвешенной средней квадратической
Cлайд 14
Структурные средние Медиана (Ме) - это величина, которая соответствует варианту, находящемуся в середине ранжированного ряда. То есть для нахождения медианы сначала необходимо определить ее порядковый номер по формуле где n - число единиц в совокупности. Численное значение медианы обычно определяют по формуле где xМе - нижняя граница медианного интервала; i - величина интервала; S-1 - накопленная частота интервала, которая предшествует медианному; f - частота медианного интервала.
Cлайд 15
Модой (Мо) называют значение признака, которое встречается наиболее часто у единиц совокупности. Чтобы найти конкретное значение моды, необходимо использовать формулу где xМо - нижняя граница модального интервала; iМо - величина модального интервала; fМо - частота модального интервала; fМо-1 - частота интервала, предшествующего модальному; fМо+1 - частота интервала, следующего за модальным. Мода имеет широкое распространение в маркетинговой деятельности при изучении покупательского спроса, особенно при определении пользующихся наибольшим спросом размеров одежды и обуви, при регулировании ценовой политики.
Cлайд 16
Показатели вариации Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию. Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей.
Cлайд 17
Абсолютные и относительные Абсолютные показатели вариации включают: размах вариации среднее линейное отклонение дисперсию среднее квадратическое отклонение Относительные показатели вариации включают: Коэффициент осцилляции Относительное линейное отклонение (линейный коэффициент вариации) Коэффициент вариации (относительное отклонение)
Cлайд 18
Графическое изображение статистических данных. Рисунок 1. Столбиковая диаграмма
Cлайд 19
Рисунок 2. Ленточная диаграмма
Cлайд 20
Рисунок 3. Структурная столбиковая диаграмма
Cлайд 21
Рисунок 4. Секторная диаграмма
Cлайд 22
Рисунок 5. Линейная диаграмма
Cлайд 23
Рисунок 6. 1 Картограмма
Cлайд 24
Рисунок 6. 2 Картограмма
Cлайд 25
Рисунок 7.1 Картодиаграмма
Cлайд 26
