Правильные многогранники

Скачать эту презентацию

Получить код Увеличить

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Много...

1 17

Презентация на тему Правильные многогранники

Скачать эту презентацию

Cлайд 1

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Правильные многогранники Платоновы тела Проектная работа по геометрии Учени 11 класса «А» 16.11.2012 http://prezentacija.biz/

Cлайд 2

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Многогранник называется правильным, если: он выпуклый; все его грани являются равными правильными многоугольниками; в каждой его вершине сходится одинаковое число рёбер.

Cлайд 3

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Определение: Правильный многогранник или платоново тело — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий пространственной симметрией.

Cлайд 4

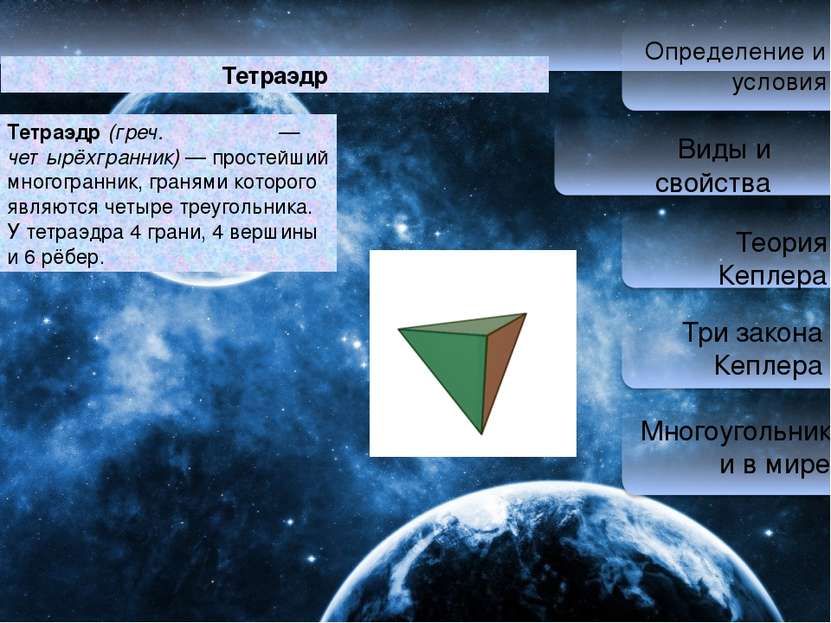
Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Тетраэдр Тетра эдр (греч. τετραεδρον — четырёхгранник) — простейший многогранник, гранями которого являются четыре треугольника. У тетраэдра 4 грани, 4 вершины и 6 рёбер.

Cлайд 5

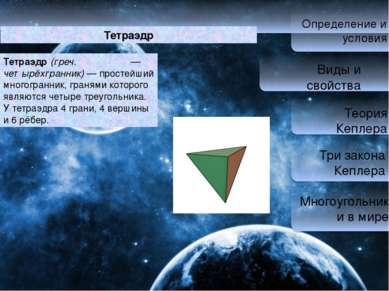Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Свойства тетраэдра: Параллельные плоскости, проходящие через пары скрещивающихся рёбер тетраэдра, определяют описанный около тетраэдра параллелепипед. Все медианы и бимедианы тетраэдра пересекаются в одной точке. Эта точка делит медианы в отношении 3:1, считая от вершины. Эта точка делит бимедианы пополам. Плоскость, проходящая через середины двух скрещивающихся рёбер тетраэдра делит его на две равные по объёму части.

Cлайд 6

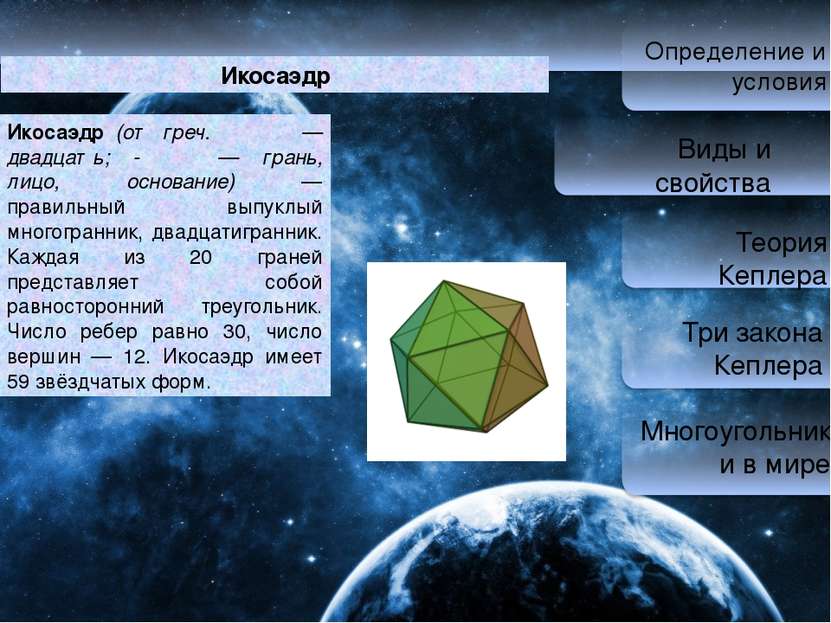
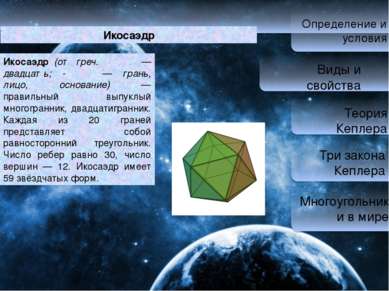
Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Икосаэдр Икоса эдр (от греч. εικοσάς — двадцать; -εδρον — грань, лицо, основание) — правильный выпуклый многогранник, двадцатигранник. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.

Cлайд 7

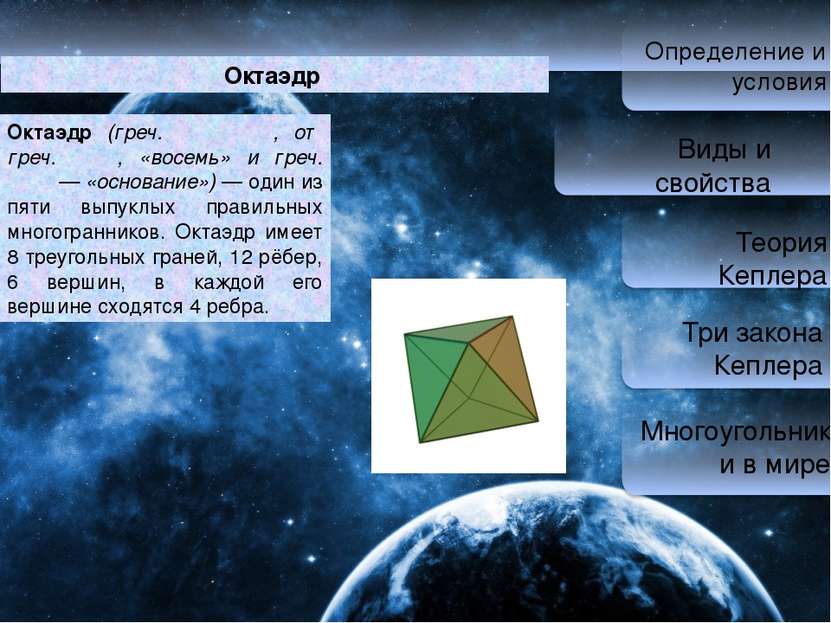
Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Октаэдр Окта эдр (греч. οκτάεδρον, от греч. οκτώ, «восемь» и греч. έδρα — «основание») — один из пяти выпуклых правильных многогранников. Октаэдр имеет 8 треугольных граней, 12 рёбер, 6 вершин, в каждой его вершине сходятся 4 ребра.

Cлайд 8

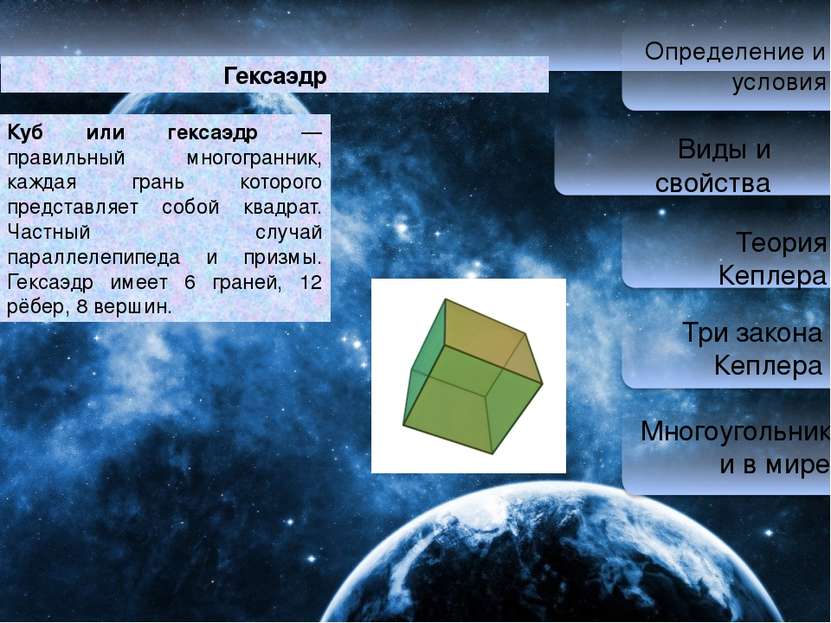
Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Гексаэдр Куб или гексаэдр — правильный многогранник, каждая грань которого представляет собой квадрат. Частный случай параллелепипеда и призмы. Гексаэдр имеет 6 граней, 12 рёбер, 8 вершин.

Cлайд 9

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Свойства куба Четыре сечения куба являются правильными шестиугольниками — эти сечения проходят через центр куба перпендикулярно четырём его главным диагоналям. В куб можно вписать тетраэдр двумя способами. В обоих случаях четыре вершины тетраэдра будут совмещены с четырьмя вершинами куба и все шесть рёбер тетраэдра будут принадлежать граням куба. В первом случае все вершины тетраэдра принадлежат граням трехгранного угла, вершина которого совпадает с одной из вершин куба. Во втором случае попарно скрещивающиеся ребра тетраэдра принадлежат попарно противолежащим граням куба. Такой тетраэдр является правильным, а его объём составляет 1/3 от объёма куба. В куб можно вписать октаэдр, притом все шесть вершин октаэдра будут совмещены с центрами шести граней куба. Куб можно вписать в октаэдр, притом все восемь вершин куба будут расположены в центрах восьми граней октаэдра. В куб можно вписать икосаэдр, при этом шесть взаимно параллельных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра — внутри куба. Все двенадцать вершин икосаэдра будут лежать на шести гранях куба.

Cлайд 10

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Додекаэдр Додека эдр (от греч. δώδεκα — двенадцать и εδρον — грань) — двенадцатигранник, составленный из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трёх правильных пятиугольников. Таким образом, додекаэдр имеет 12 граней (пятиугольных), 30 рёбер и 20 вершин (в каждой сходятся 3 ребра). Сумма плоских углов при каждой из 20 вершин равна 324°. Додекаэдр имеет три звёздчатые формы.

Cлайд 11

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Теория Кеплера Сначала Кеплера соблазнила мысль о том, что существует всего пять правильных многогранников и всего шесть (как казалось тогда) планет Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн. Показалось, что гармония мира и любовь природы к повторениям сделали правильные многогранники связующими звеньями между шестью небесными телами. Кеплер предположил, что сферы планет связаны между собой вписанными в них Платоновыми телами. Так как для каждого правильного многогранника центры вписанной и описанной сфер совпадают, то вся модель будет иметь единый центр, в котором располагается Солнце.

Cлайд 12

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Три закона движения планет Кеплера: На основе обобщения данных, полученных в результате наблюдений, он установил три закона движения планет относительно Солнца. Первый закон: каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Второй закон: каждая планета движется в плоскости, проходящей через центр Солнца, причем площадь сектора орбиты, описанная радиусом-вектором, изменяется пропорционально времени. Третий закон: квадраты времени обращения планеты вокруг Солнца относятся, как кубы их средних расстояний от Солнца. Но это были только гипотезы, пока их не объяснил и уточнил на основе закона всемирного тяготения Исаак Ньютон (1643-1727), создавший теорию движения небесных тел, которая доказала свою жизнеспособность тем, что с ее помощью люди научились предсказывать многие небесные явления.

Cлайд 13

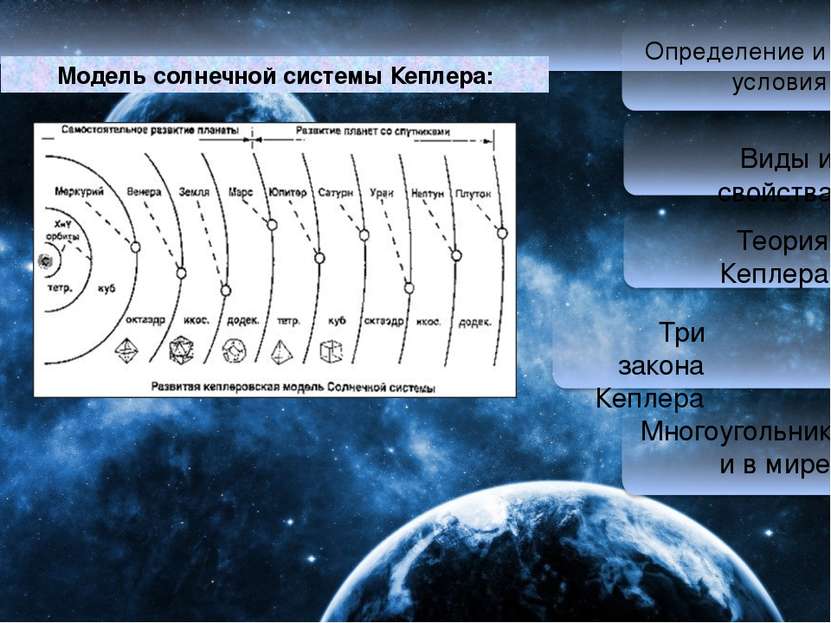
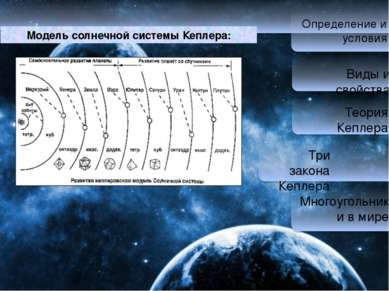
Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Модель солнечной системы Кеплера:

Cлайд 14

Определение и условия Виды и свойства Теория Кеплера Три закона Кеплера Многоугольники в мире Многоугольники в окружающем мире Правильные многогранники встречаются в совершенно разных науках и везде в окружающем мире: Молекулы веществ в химии тела вирусов Игральные кости А так же и в других совершенно различных местах нашей вселенной, например Платон сопоставлял додекаэдр с моделью нашей вселенной. О нём он писал: «…его бог определил для Вселенной и прибегнул к нему в качестве образца»

Cлайд 15