X
Код презентации скопируйте его
Определение расстояний до тел Солнечной системы.
Скачать эту презентацию
Презентация на тему Определение расстояний до тел Солнечной системы.
Скачать эту презентациюCлайд 1
Определение расстояний до тел Солнечной системы.
Cлайд 2
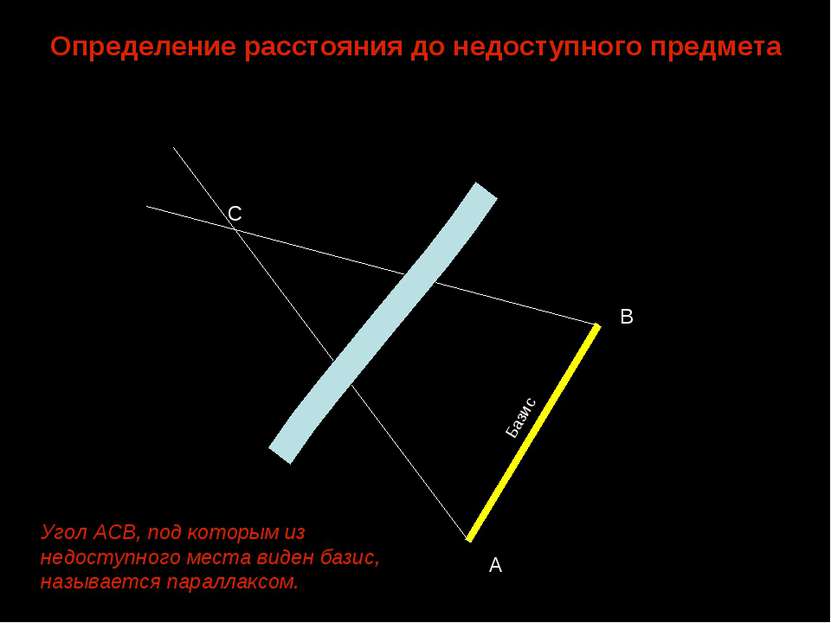
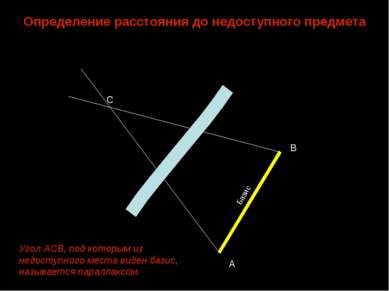Определение расстояния до недоступного предмета С А В Базис Угол АСВ, под которым из недоступного места виден базис, называется параллаксом.
Cлайд 3
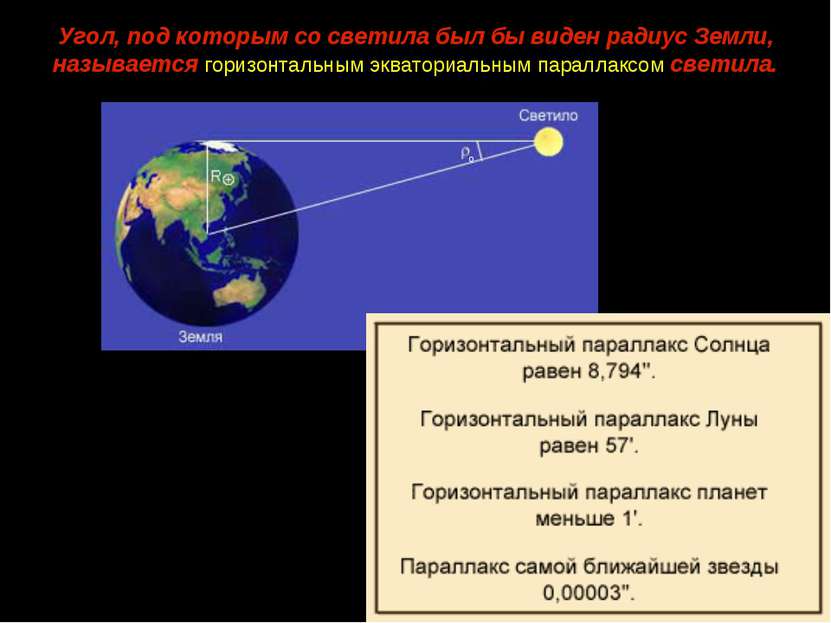
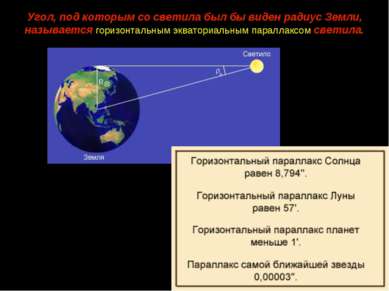Угол, под которым со светила был бы виден радиус Земли, называется горизонтальным экваториальным параллаксом светила. о
Cлайд 4
D Углы pо малы, поэтому их синусы можно заменить самими углами, т.е. sin pо ≈ pо если величина угла выражена в радианах. Если pо выражен в секундах дуги, то sin pо ≈ pо / 206 265 ”, т.к. 1 радиан = 57,3o = 3 438 ’ = 206 265 ”. Поэтому расстояние до светила определяют по формуле Определение расстояния до светила о о о
Cлайд 5
Дано: Найти: Решение: Ответ: p = 57’02’’ D D = 206 265‘‘ * R⊕ / p ≈ 384 400 км R⊕ = 6378 км D = 206 265‘‘ * 6378 км / 3422‘‘ D ≈ 384 400 км D Задача. Зная горизонтальный параллакс Луны и экваториальный радиус Земли (6378 км), найти расстояние от Земли до Луны.
Cлайд 6
Радиолокационный метод определения расстояний до планет. Посылают кратковременный импульс, который затем принимают после отражения. Скорость распространения радиоволн равна скорости света в вакууме: с = 299 792 458 м/с. Из радиолокационных наблюдений Венеры получено следующее значение астрономической единицы: 1 а.е. = 149 597 868 ± 0,7 км
Cлайд 7
Вычисление линейных размеров тел Солнечной системы R = D sin R⊕ = D sin po R = R⊕ sin / sin po R = R⊕ / po R о о R D - угловой радиус небесного тела Задача. Во сколько раз линейный радиус Солнца превышает радиус Земли, если угловой радиус Солнца 16’? Дано: Найти: Решение: Ответ: = 16’ R R = R⊕ / p ≈ 109 R⊕ p = 8,8” R = (16*60”/8,8”) R⊕ ≈ 109 R⊕
Cлайд 8
Конец!!!
