X
Код презентации скопируйте его
Задачи на построение (7 класс)
Скачать эту презентациюПрезентация на тему Задачи на построение (7 класс)
Скачать эту презентациюCлайд 2
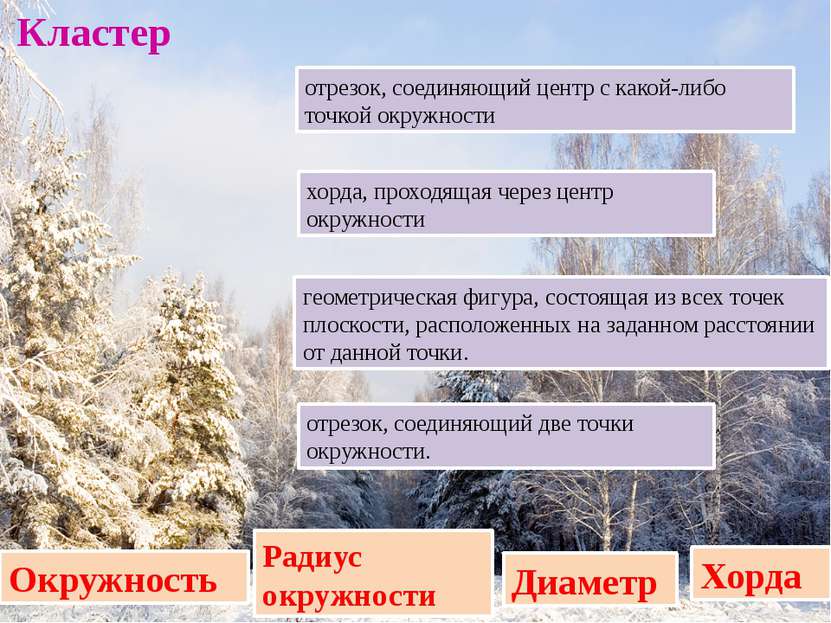
 Окружность геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Радиус окружности отрезок, соединяющий центр с какой-либо точкой окружности отрезок, соединяющий две точки окружности. Хорда хорда, проходящая через центр окружности Диаметр Кластер
Окружность геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки. Радиус окружности отрезок, соединяющий центр с какой-либо точкой окружности отрезок, соединяющий две точки окружности. Хорда хорда, проходящая через центр окружности Диаметр Кластер
Cлайд 3
 Анализ. Нарисовать фигуру, установить связь между данными задачи и искомыми элементами, составить план решения задачи. Построение. Выполняется по намеченному плану выполняется циркулем и линейкой. Доказательство. Доказать, что построенная фигура удовлетворяет условиям задачи. Исследование. Выяснить при любых ли данных задача имеет решение, и если имеет, то сколько решений. Алгоритм решения задач на построение
Анализ. Нарисовать фигуру, установить связь между данными задачи и искомыми элементами, составить план решения задачи. Построение. Выполняется по намеченному плану выполняется циркулем и линейкой. Доказательство. Доказать, что построенная фигура удовлетворяет условиям задачи. Исследование. Выяснить при любых ли данных задача имеет решение, и если имеет, то сколько решений. Алгоритм решения задач на построение
Cлайд 4
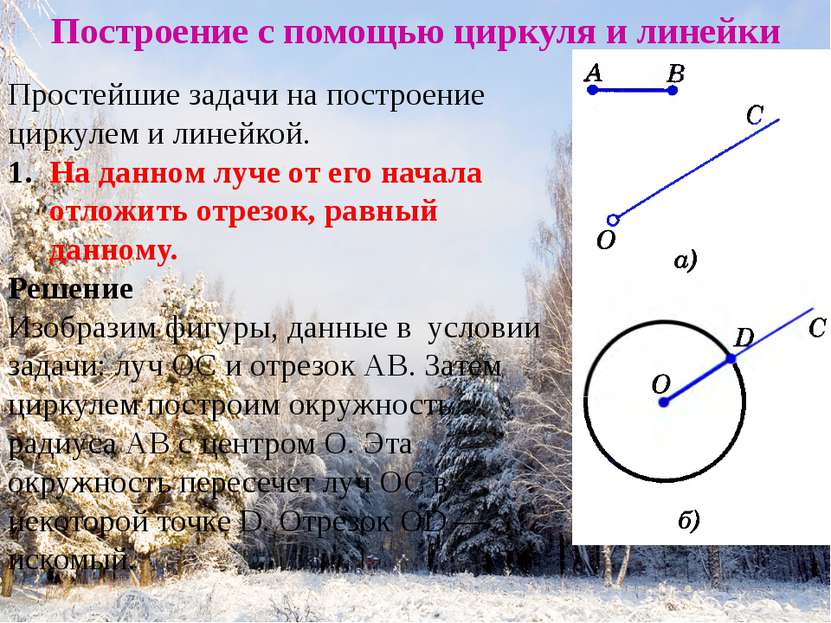
 Построение с помощью циркуля и линейки Простейшие задачи на построение циркулем и линейкой. На данном луче от его начала отложить отрезок, равный данному. Решение Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ. Затем циркулем построим окружность радиуса АВ с центром О. Эта окружность пересечет луч ОС в некоторой точке D. Отрезок OD — искомый.
Построение с помощью циркуля и линейки Простейшие задачи на построение циркулем и линейкой. На данном луче от его начала отложить отрезок, равный данному. Решение Изобразим фигуры, данные в условии задачи: луч ОС и отрезок АВ. Затем циркулем построим окружность радиуса АВ с центром О. Эта окружность пересечет луч ОС в некоторой точке D. Отрезок OD — искомый.
Cлайд 5
 Построение с помощью циркуля и линейки 2. Отложить от данного луча угол, равный данному. Решение Данный угол с вершиной А и луч ОМ изображены на рисунке. Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ. Проведем окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С (рис. а). Затем проведем окружность того же радиуса с центром в начале данного луча ОМ. Она пересекает луч в точке D (рис. б). После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е.
Построение с помощью циркуля и линейки 2. Отложить от данного луча угол, равный данному. Решение Данный угол с вершиной А и луч ОМ изображены на рисунке. Требуется построить угол, равный углу А, так, чтобы одна из его сторон совпала с лучом ОМ. Проведем окружность произвольного радиуса с центром в вершине А данного угла. Эта окружность пересекает стороны угла в точках В и С (рис. а). Затем проведем окружность того же радиуса с центром в начале данного луча ОМ. Она пересекает луч в точке D (рис. б). После этого построим окружность с центром D, радиус которой равен ВС. Окружности с центрами О и D пересекаются в двух точках. Одну из этих точек обозначим буквой Е.
Cлайд 6
 Построение с помощью циркуля и линейки 2. Отложить от данного луча угол, равный данному. Докажем, что угол МОЕ — искомый. Рассмотрим треугольники ABC и ODE. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки OD и ОЕ — радиусами окружности с центром О (см. рис. б). Так как по построению эти окружности имеют равные радиусы, то AB = OD, АС = ОЕ. Также по построению ВС = DE. Следовательно, ABC = ODE по трем сторонам. Поэтому DOE = BAC, т. е. построенный угол МОЕ равен данному углу А.
Построение с помощью циркуля и линейки 2. Отложить от данного луча угол, равный данному. Докажем, что угол МОЕ — искомый. Рассмотрим треугольники ABC и ODE. Отрезки АВ и АС являются радиусами окружности с центром А, а отрезки OD и ОЕ — радиусами окружности с центром О (см. рис. б). Так как по построению эти окружности имеют равные радиусы, то AB = OD, АС = ОЕ. Также по построению ВС = DE. Следовательно, ABC = ODE по трем сторонам. Поэтому DOE = BAC, т. е. построенный угол МОЕ равен данному углу А.
Cлайд 11
 Синквейн Окружность Круглая, имеющая центр, радиус, диаметр, хорду, Берем циркуль, чертим, отмечаем центр все точки равноудаленные от данной точки плоскости Похожа на обруч!
Синквейн Окружность Круглая, имеющая центр, радиус, диаметр, хорду, Берем циркуль, чертим, отмечаем центр все точки равноудаленные от данной точки плоскости Похожа на обруч!
Cлайд 12
 Построение с помощью циркуля и линейки Решение простейших задач на построение циркулем и линейкой. 1. На данном луче от его начала отложить отрезок, равный данному. 2. Отложить от данного луча угол, равный данному. 3. Построить биссектрису данного неразвернутого угла. 4. Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка. 5. Построить середину данного отрезка. 6. Даны прямая и точка, не лежащая на ней. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой (решение в учебнике задачи № 153). 7. Решить задачи №№ 148, 150, 155.
Построение с помощью циркуля и линейки Решение простейших задач на построение циркулем и линейкой. 1. На данном луче от его начала отложить отрезок, равный данному. 2. Отложить от данного луча угол, равный данному. 3. Построить биссектрису данного неразвернутого угла. 4. Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка. 5. Построить середину данного отрезка. 6. Даны прямая и точка, не лежащая на ней. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой (решение в учебнике задачи № 153). 7. Решить задачи №№ 148, 150, 155.