X
Код презентации скопируйте его
Правильный многоугольник
Скачать эту презентацию
Презентация на тему Правильный многоугольник
Скачать эту презентациюCлайд 1
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ Работу выполнила учитель математики МОУ СОШ № 5 г. Кстово Нижегородской области Гущина Татьяна Леонидовна 2012 г.
Cлайд 2
СОДЕРЖАНИЕ Из истории Общие сведения Правильные многогранники Паркеты из правильных многоугольников Правильные многоугольники в природе Симметрия правильных многоугольников выход
Cлайд 3
Из истории Правильные многоугольники были известны еще в глубокой древности. В египетских и вавилонских старинных памятниках встречаются правильные четырехугольники, шестиугольники и восьмиугольники в виде изображений на стенах и украшений, высеченных их камня. Древнегреческие ученые стали проявлять большой интерес к правильным многоугольникам еще со времен Пифагора. Учение о правильных многоугольниках было систематизировано и изложено в 4 книге «Начал» Евклида.
Cлайд 4
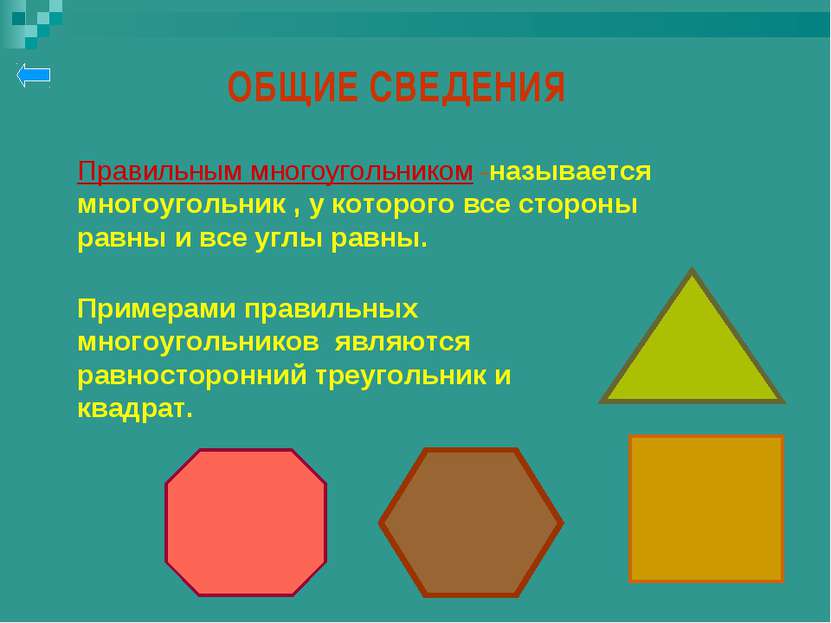
ОБЩИЕ СВЕДЕНИЯ Правильным многоугольником -называется многоугольник , у которого все стороны равны и все углы равны. Примерами правильных многоугольников являются равносторонний треугольник и квадрат.
Cлайд 5
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ ПЛАТОНОВЫ тела: Тетраэдр – «огонь» Куб– «земля» Октаэдр – «воздух» Додекаэдр – «весь мир» Икосаэдр – «вода» 4 6 8 12 20
Cлайд 6
РАЗВЕРТКИ ПРАВИЛЬНЫХ МНОГОГРАННИКОВ Можно сделать модель правильного многогранника, используя его развертку.
Cлайд 7
ПАРКЕТЫ ИЗ ПРАВИЛЬНЫХ МНОГОУГОЛЬНИКОВ Паркеты из одинаковых правильных многоугольников Паркеты из разных правильных многоугольников
Cлайд 8
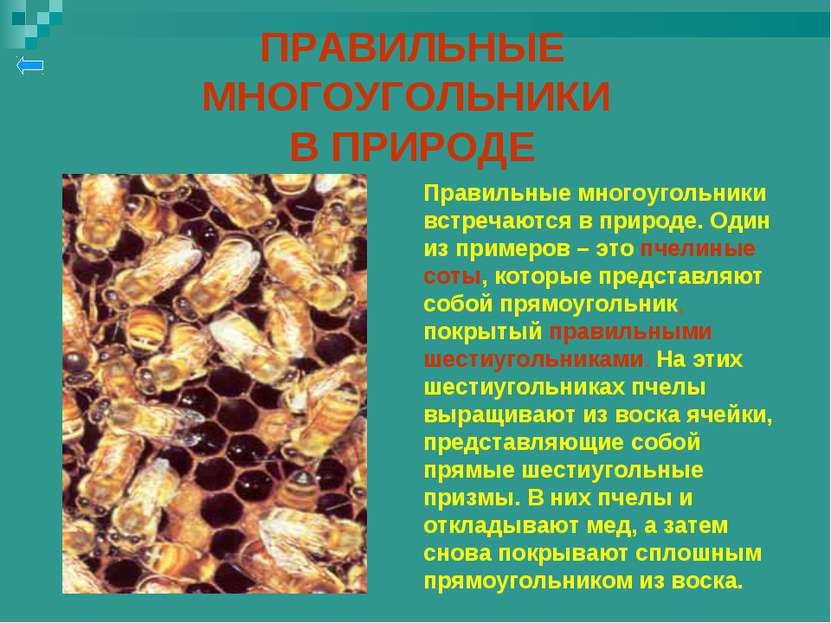
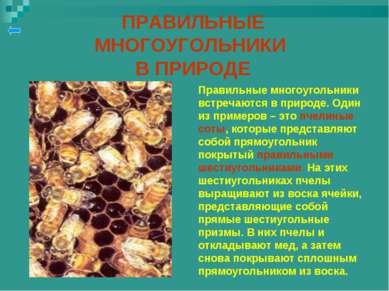ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ Правильные многоугольники встречаются в природе. Один из примеров – это пчелиные соты, которые представляют собой прямоугольник, покрытый правильными шестиугольниками. На этих шестиугольниках пчелы выращивают из воска ячейки, представляющие собой прямые шестиугольные призмы. В них пчелы и откладывают мед, а затем снова покрывают сплошным прямоугольником из воска.
Cлайд 9
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ Снежинки имеют форму правильных многоугольников
Cлайд 10
ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ В ПРИРОДЕ Многие простейшие морские организмы ( радиолярии ) имеют форму правильных многоугольников
Cлайд 11
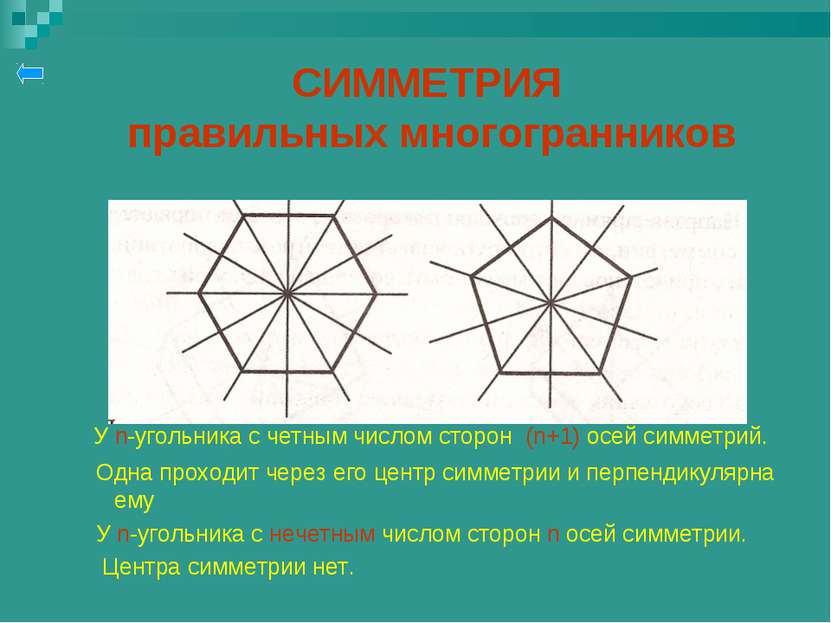
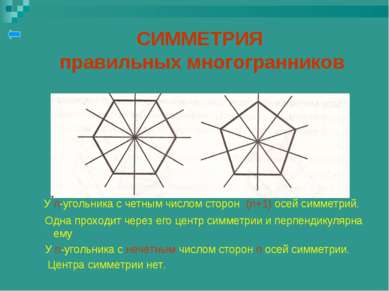СИММЕТРИЯ правильных многогранников У n-угольника с четным числом сторон (n+1) осей симметрий. Одна проходит через его центр симметрии и перпендикулярна ему У n-угольника с нечетным числом сторон n осей симметрии. Центра симметрии нет.
Cлайд 12
ЗВЕЗЧАТЫЕ МНОГОУГОЛЬНИКИ 5-угольник 8-угольник
Cлайд 13
МАТЕМАТИКА…выявляет порядок, симметрию и определенность, а это важнейшие виды прекрасного. Аристотель
Cлайд 14
Источники информации: Детская энциклопедия "Я познаю мир" Математика, Москва, АСТ,1998. ru.wikipedia.org/wiki/История математики А..И.Азевич Двадцатьуроков гармонии: Гуманитарно-математический курс.-М.: Школа-Пресс,1998.
