X
Код презентации скопируйте его
Призма. Построение сечений призмы плоскостями
Скачать эту презентацию
Презентация на тему Призма. Построение сечений призмы плоскостями
Скачать эту презентациюCлайд 1
Призма. Построение сечений призмы плоскостями. Урок изучения нового материала. Геометрия 10 класс. Учебник: Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Л.С. Киселёва, Э.Г. Позняк «Геометрия «10-11» Автор: Кузнецова Валентина Ивановна, учитель математики, высшая квалификационная категория. Место работы: МОУ «Покровская средняя общеобразовательная школа» Красногородский район Псковская область
Cлайд 2
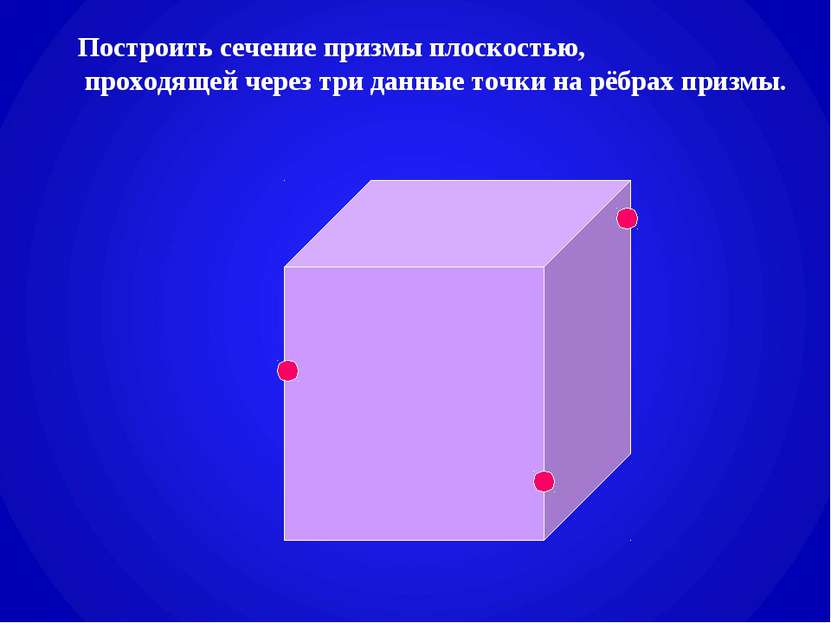
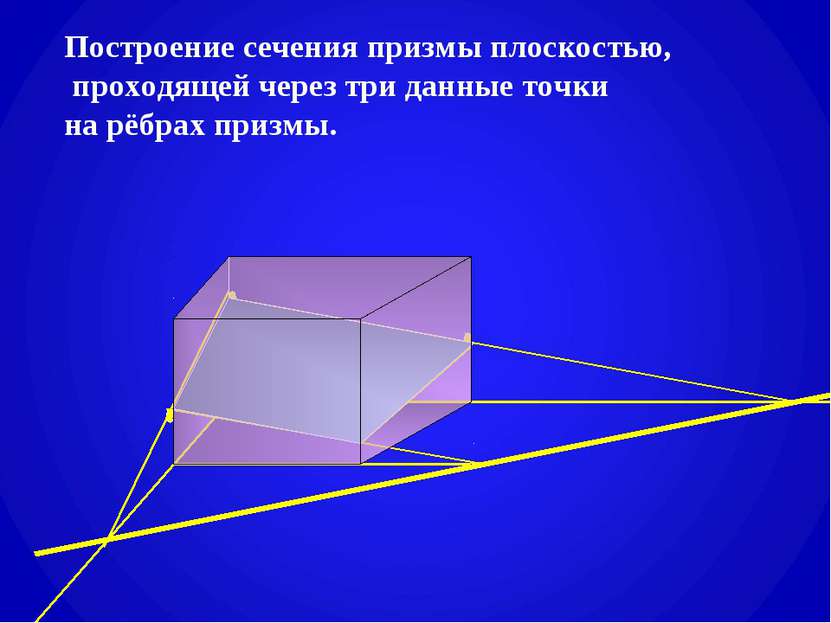
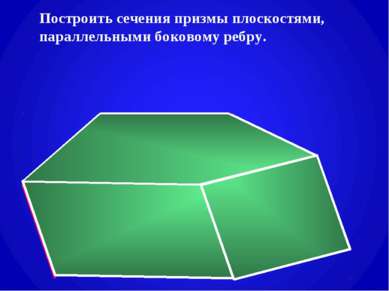
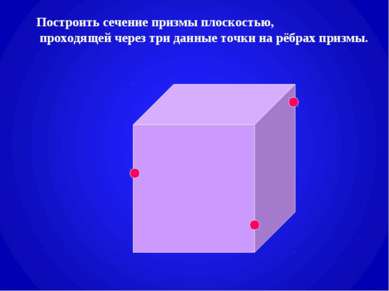
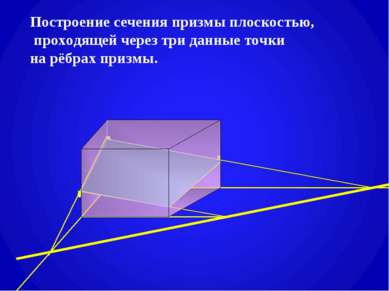
План урока. Тема: Призма. Построение сечений призмы плоскостями. Цель: Дать определение призмы. Научить строить сечения призмы плоскостями. Оборудование: мультимедийный проектор. Ход урока: 1. Изучение нового материала. 1). Определение призмы и ей изображение. Различные виды призм (слайды №3,4). 2). Построение сечений призмы плоскостью, а) проходящей через два боковых ребра, не принадлежащих одной грани (слайд №5), б) параллельной боковому ребру (самостоятельно с последующей проверкой) (слайд №6), в) проходящей через след секущей плоскости (слайды № 7,8,9), г) проходящей через три данные точки на рёбрах призмы (слайды №10,11). 2. Закрепление изученного. Самостоятельная работа по карточке с последующей проверкой : построить сечение призмы плоскостью, проходящей через данную точку м след секущей плоскости (слайд №12). 3. Итог урока. 4. Домашнее задние. Построить сечение призмы (карточки с заданием).
Cлайд 3
Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников. Многоугольники – основания призмы; Отрезки, соединяющие соответствующие вершины – боковые рёбра призмы.
Cлайд 4
Различные виды призм.
Cлайд 5
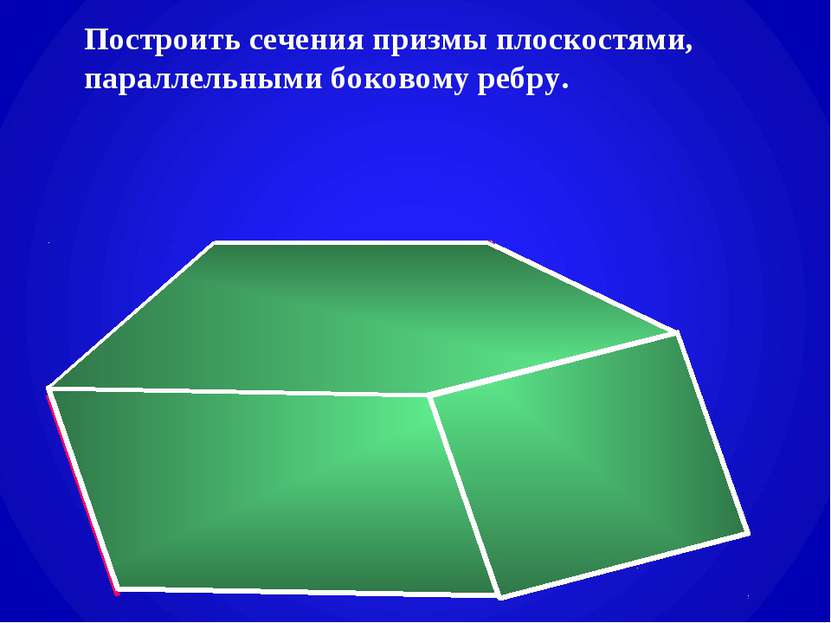
Сечения призмы плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани.
Cлайд 6
Построить сечения призмы плоскостями, параллельными боковому ребру.
Cлайд 7
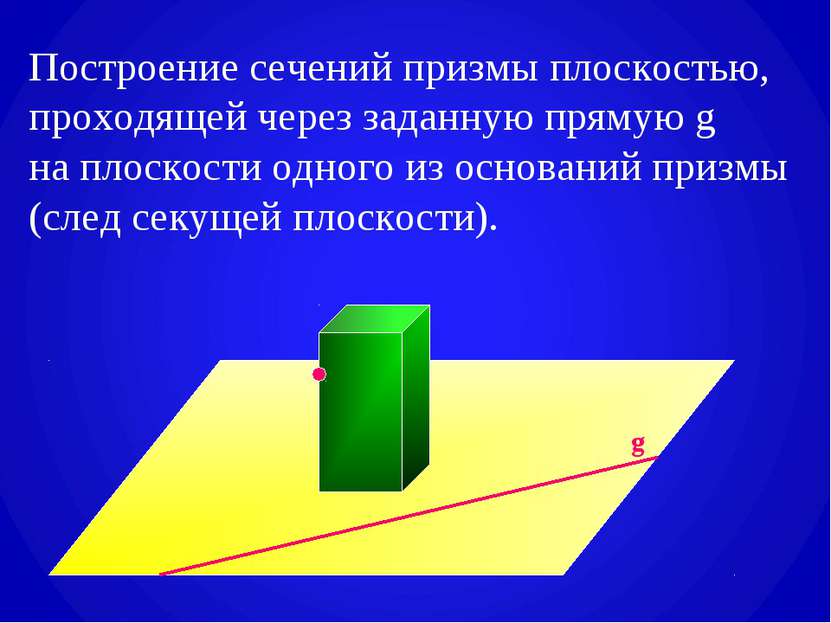
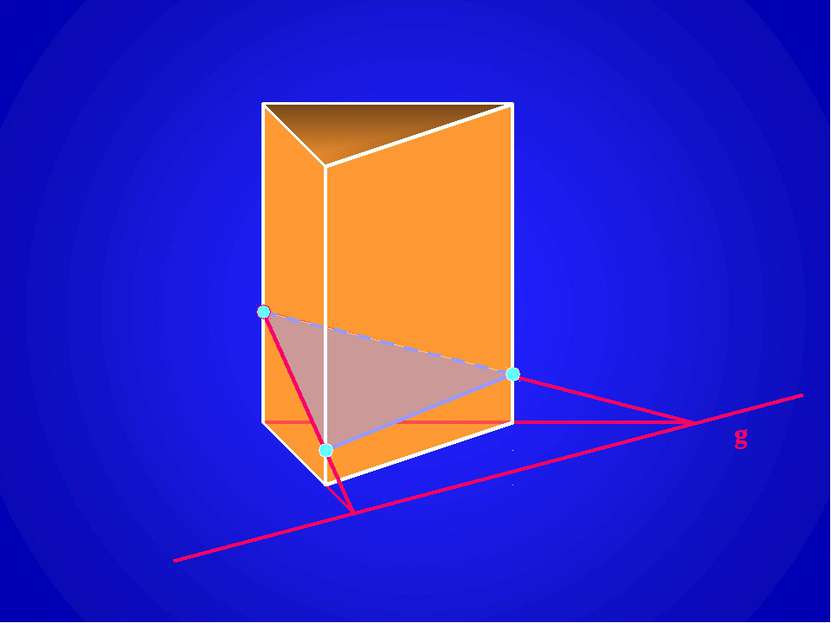
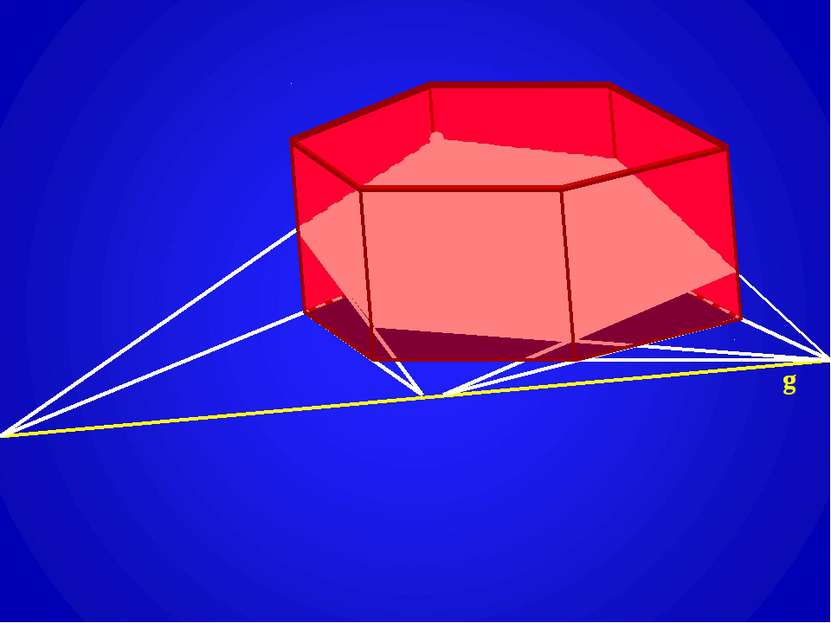
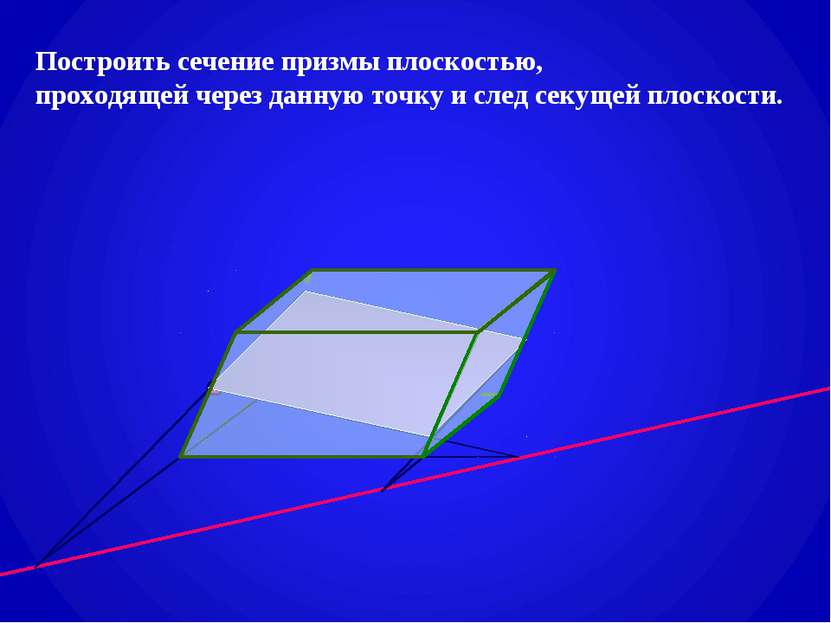
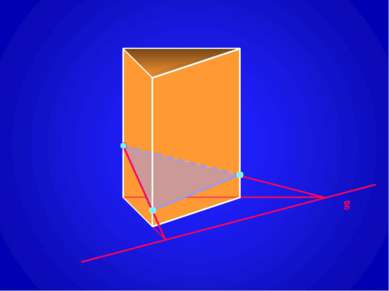
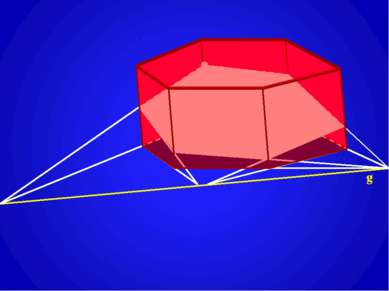
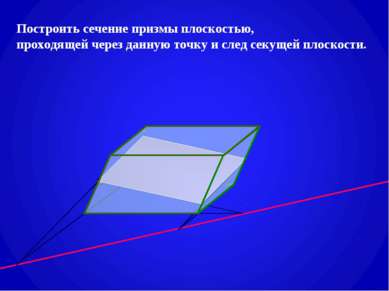
Построение сечений призмы плоскостью, проходящей через заданную прямую g на плоскости одного из оснований призмы (след секущей плоскости). g
Cлайд 8
g
Cлайд 9
g
Cлайд 10
Построить сечение призмы плоскостью, проходящей через три данные точки на рёбрах призмы.
Cлайд 11
Построение сечения призмы плоскостью, проходящей через три данные точки на рёбрах призмы.
Cлайд 12
Построить сечение призмы плоскостью, проходящей через данную точку и след секущей плоскости.
Cлайд 13
