X
Код презентации скопируйте его
Повторение геометрии при подготовке к итоговой аттестации
Скачать эту презентацию
Презентация на тему Повторение геометрии при подготовке к итоговой аттестации
Скачать эту презентациюCлайд 1
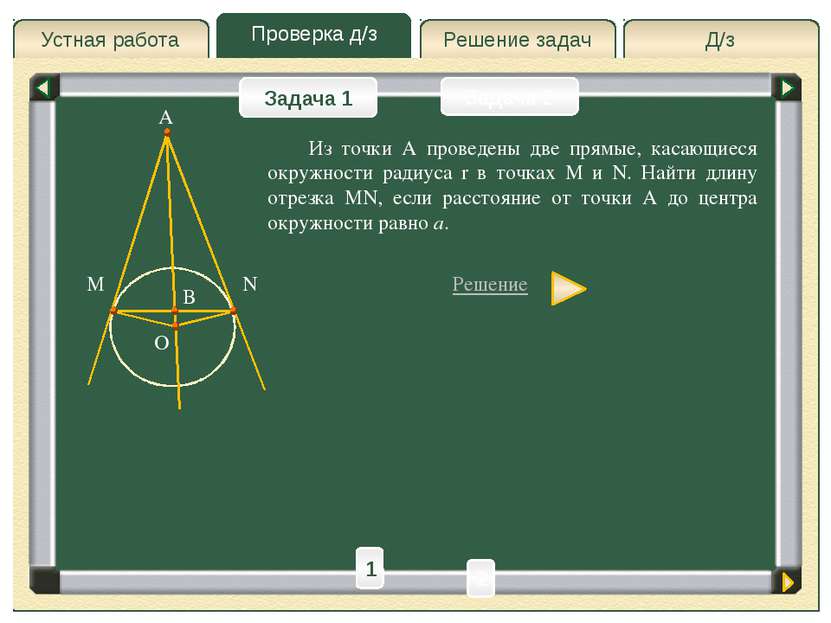
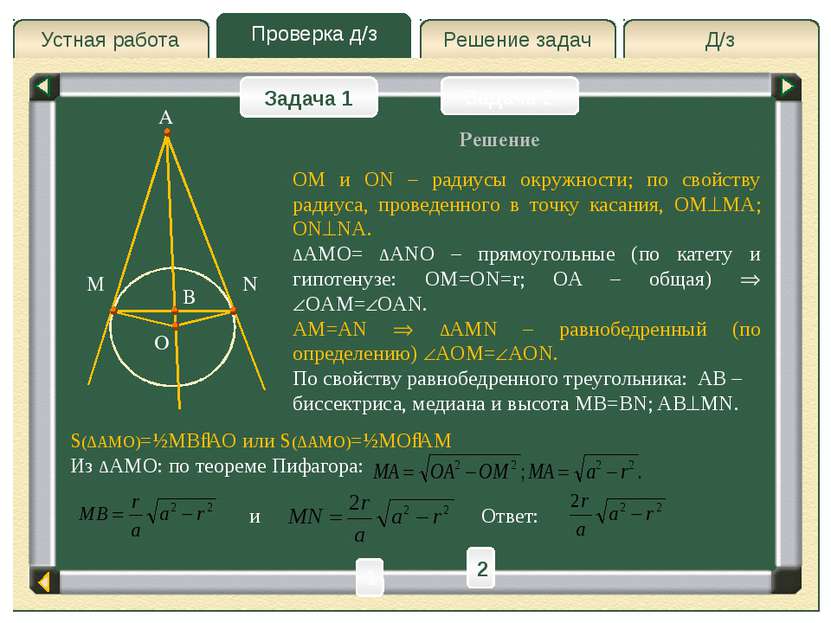
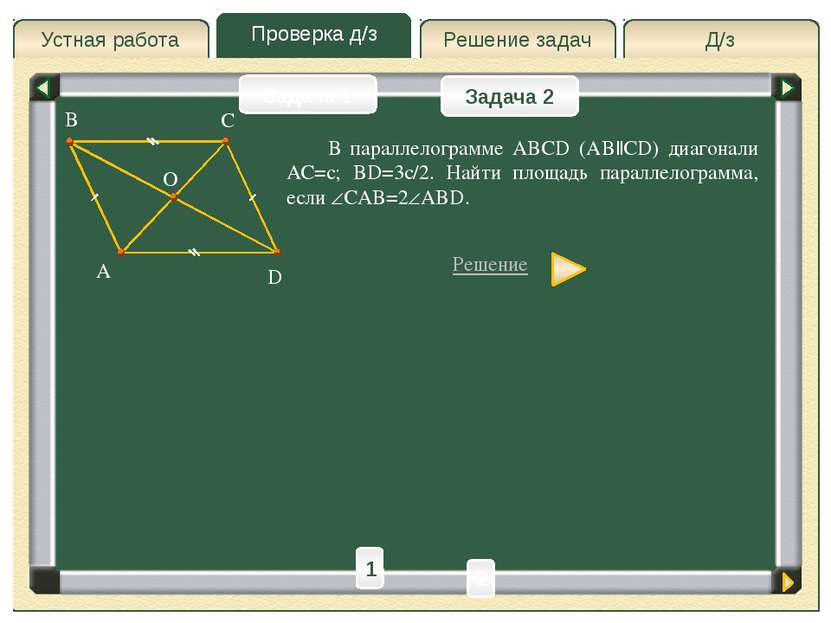
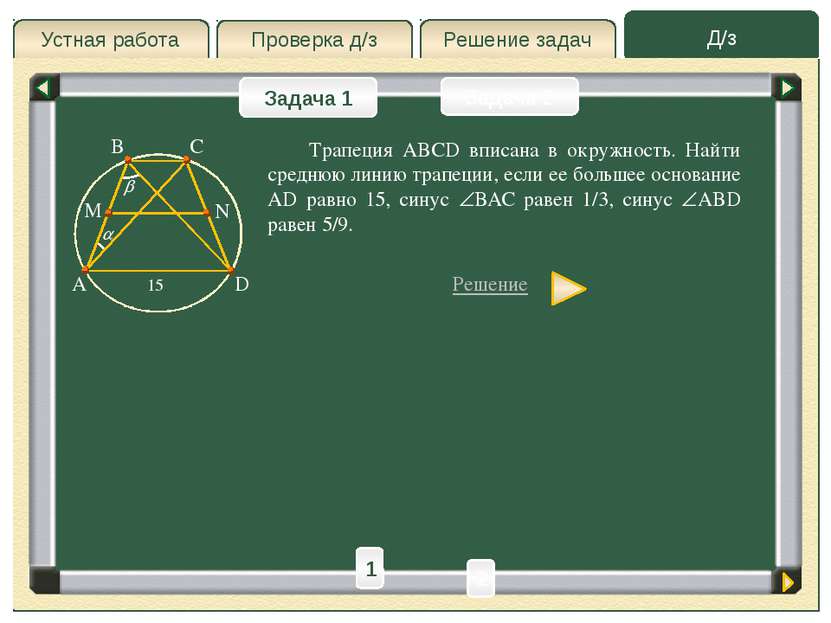
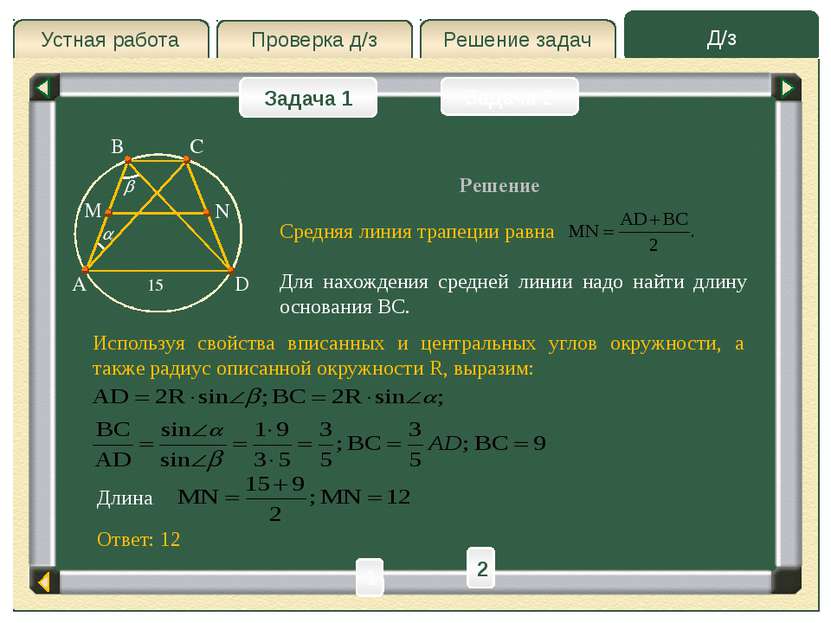
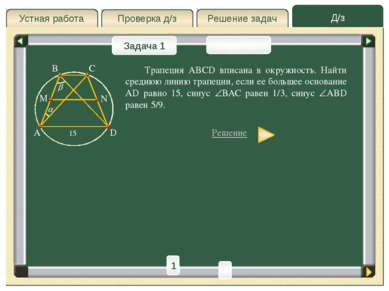
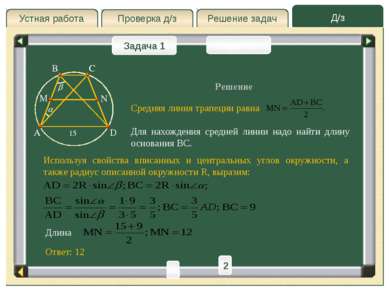
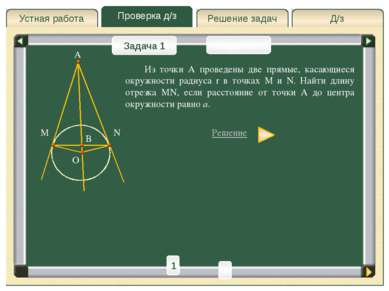
Д/з Решение задач Проверка д/з Устная работа Проверка д/з Задача 1 Задача 2 Из точки А проведены две прямые, касающиеся окружности радиуса r в точках M и N. Найти длину отрезка MN, если расстояние от точки A до центра окружности равно a. Решение A M N O B 1 2
Cлайд 2
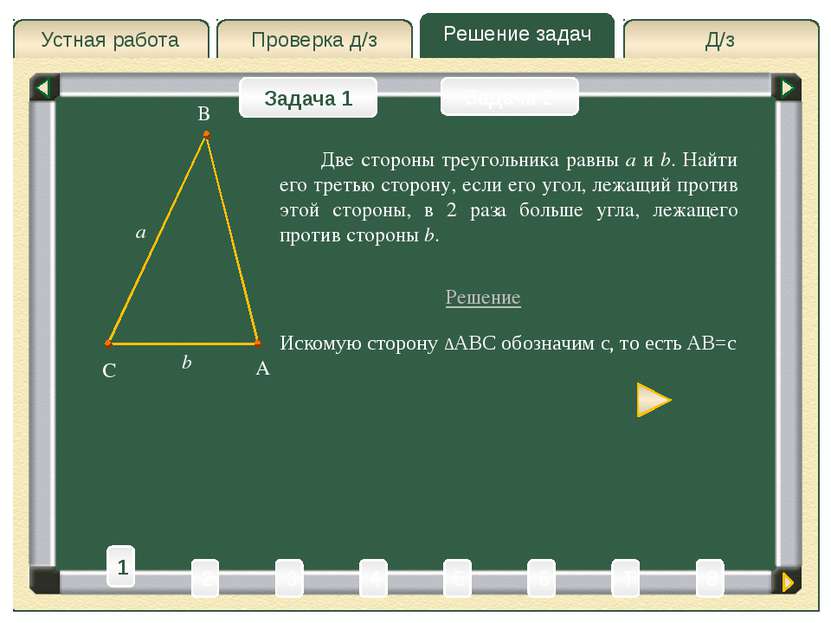
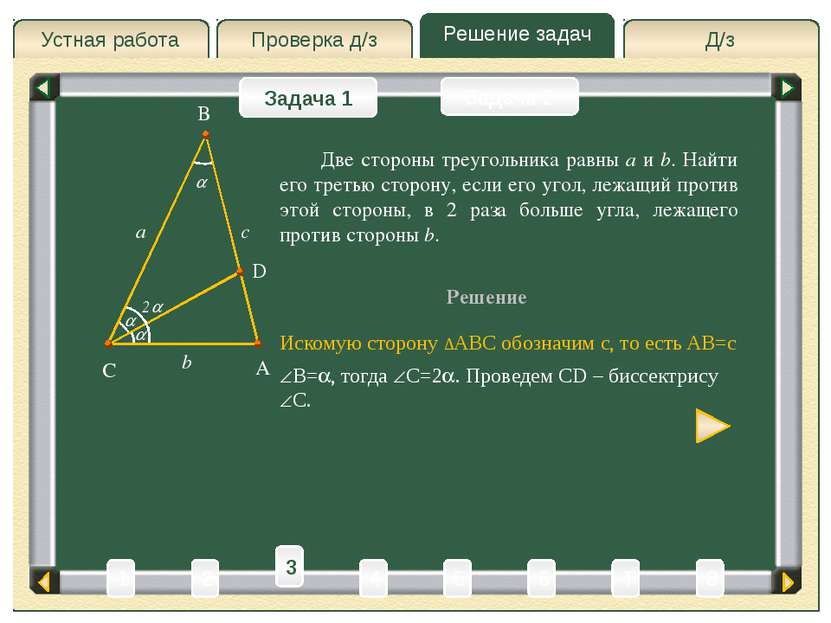
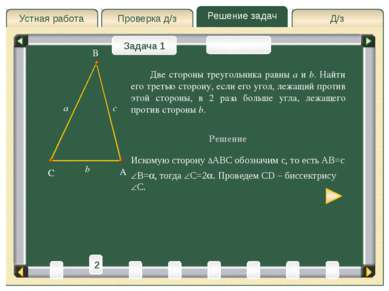
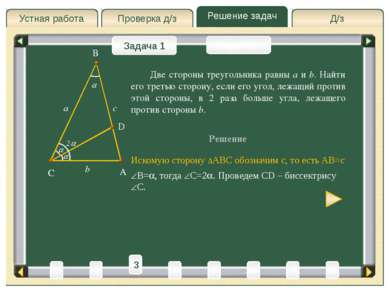
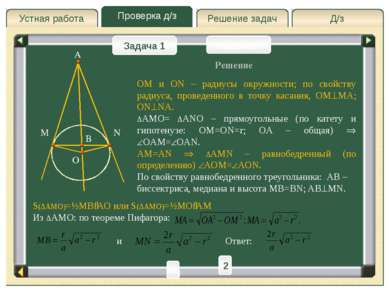
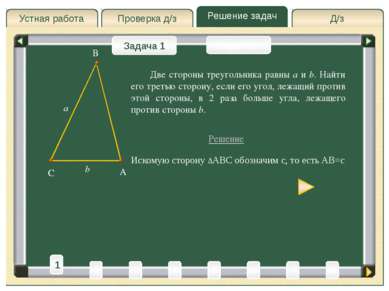
Д/з Проверка д/з Решение задач Устная работа Проверка д/з Задача 1 Задача 2 Две стороны треугольника равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b. Решение A C B a b Искомую сторону ∆ABC обозначим c, то есть AB=c 3 4 5 2 6 8 T 1
Cлайд 3
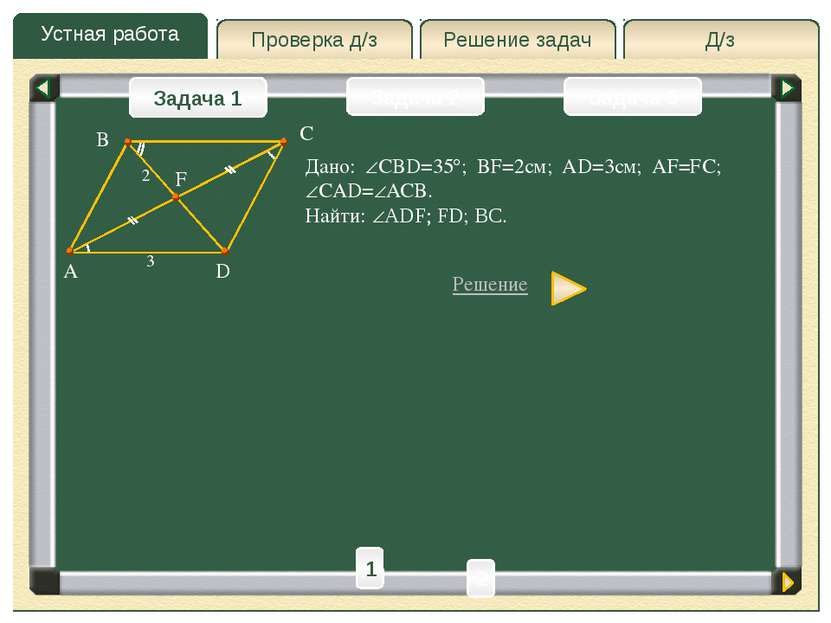
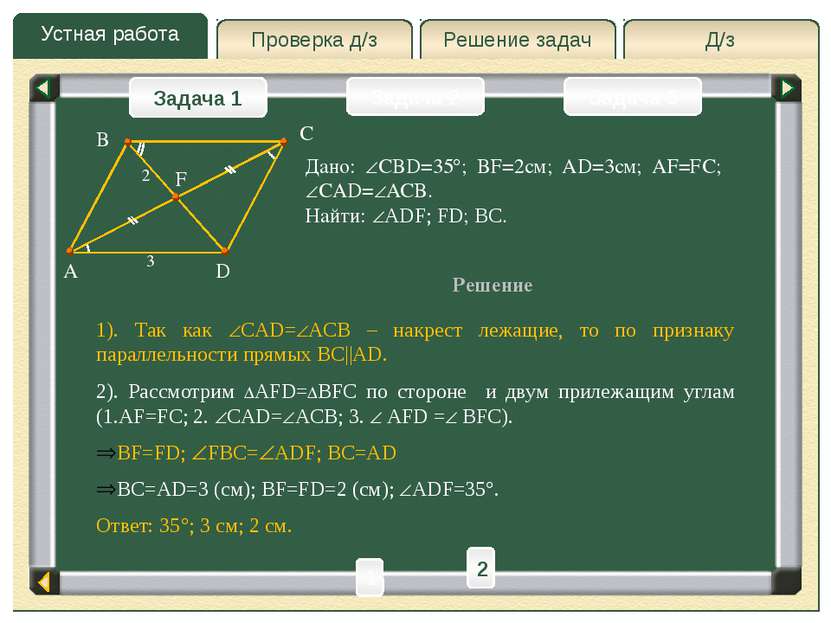
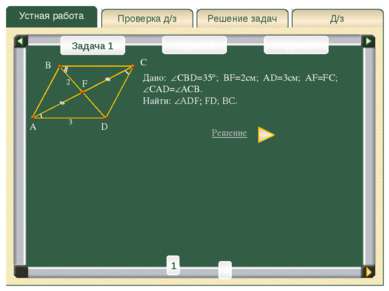
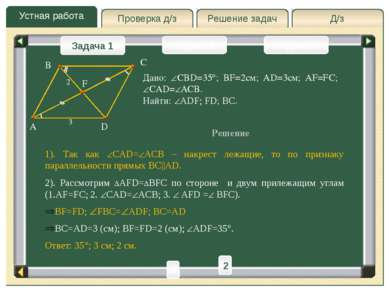Устная работа Д/з Решение задач Проверка д/з Задача 1 Задача 2 Задача 3 Дано: CBD=35 ; BF=2см; AD=3см; AF=FC; CAD= ACB. Найти: ADF; FD; BC. Решение A C D F B 3 2 1 2
Cлайд 4
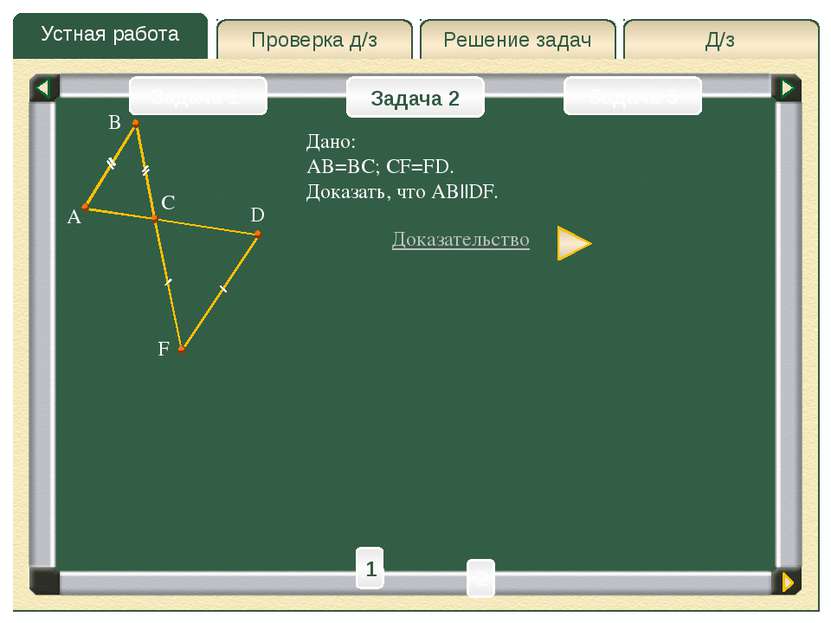
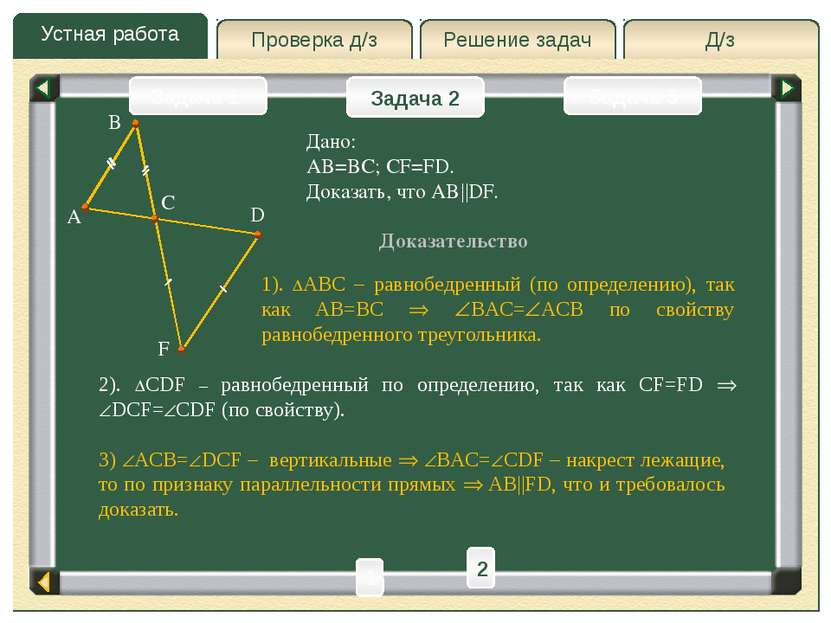
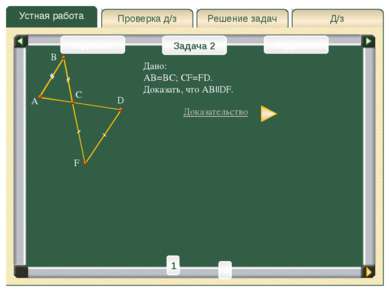Д/з Решение задач Устная работа Проверка д/з Задача 2 Задача 1 Задача 3 A D F B Дано: AB=BC; CF=FD. Доказать, что AB||DF. Доказательство C 1 2
Cлайд 5
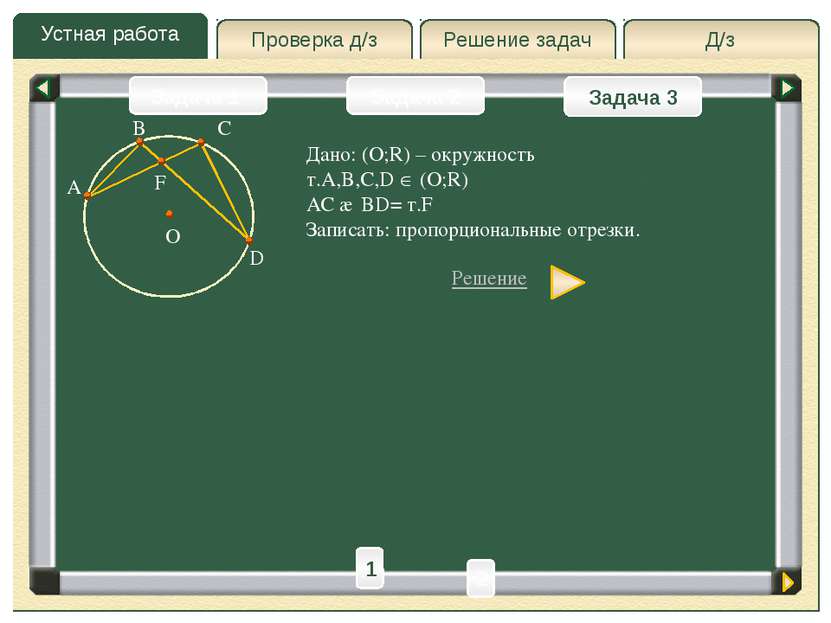
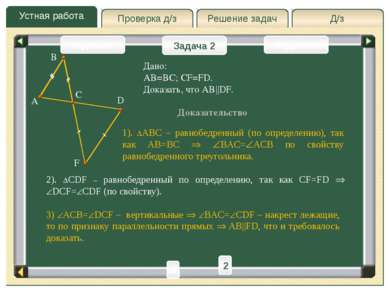Д/з Решение задач Устная работа Проверка д/з Задача 2 Задача 3 Задача 1 B A C O D F Дано: (O;R) – окружность т.A,B,C,D (O;R) AC ∩ BD= т.F Записать: пропорциональные отрезки. Решение 1 2
Cлайд 6
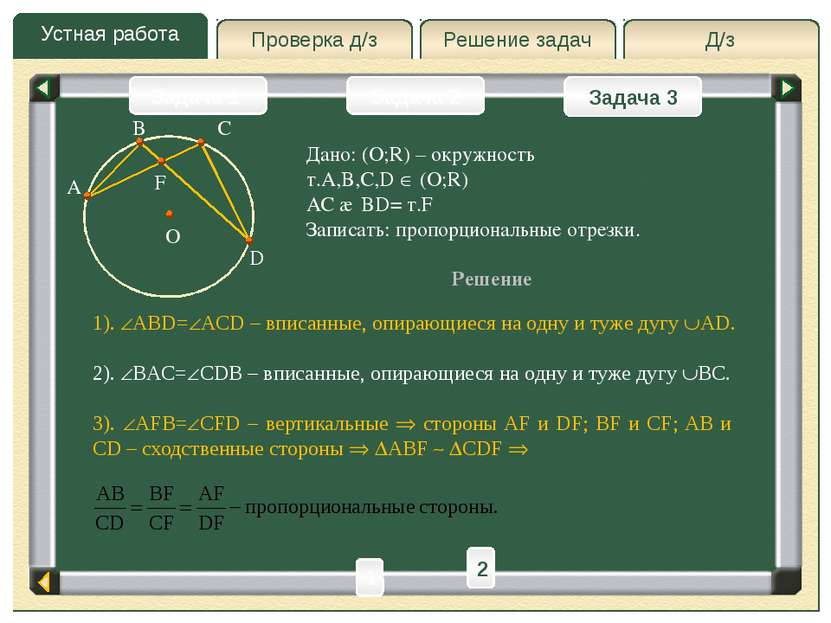
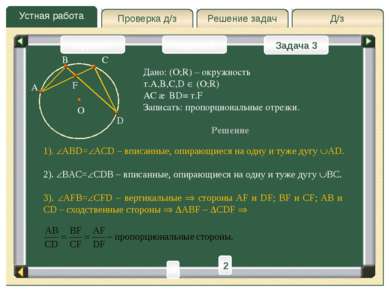
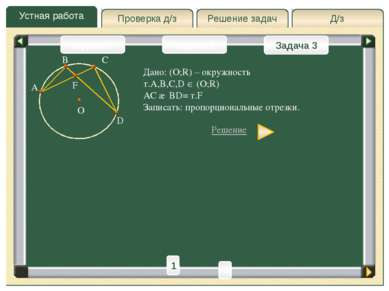Д/з Решение задач Устная работа Проверка д/з Задача 2 Задача 3 Задача 1 B A C O D F Дано: (O;R) – окружность т.A,B,C,D (O;R) AC ∩ BD= т.F Записать: пропорциональные отрезки. Решение 1). ABD= ACD – вписанные, опирающиеся на одну и туже дугу AD. 2). BAC= CDB – вписанные, опирающиеся на одну и туже дугу BC. 3). AFB= CFD – вертикальные стороны AF и DF; BF и CF; AB и CD – сходственные стороны ABF CDF 2 1
Cлайд 7
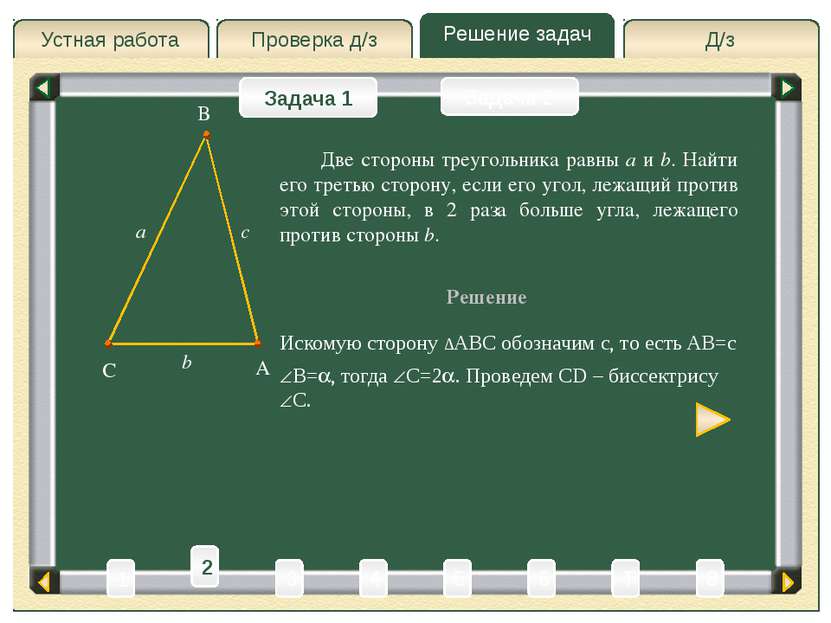
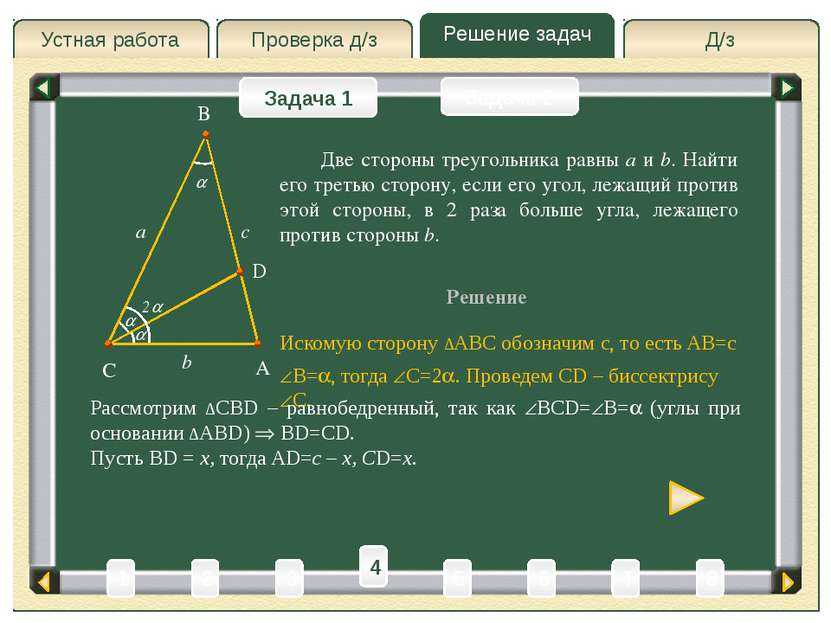
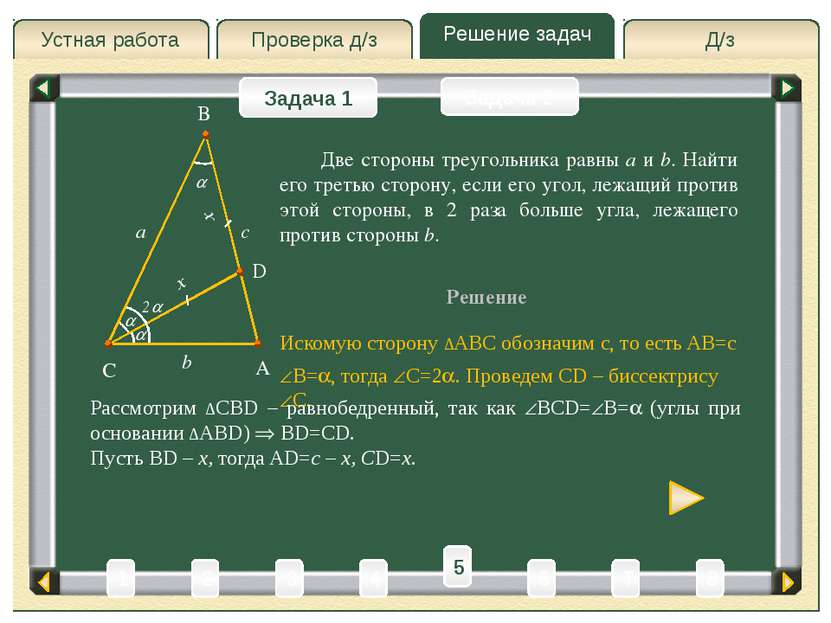
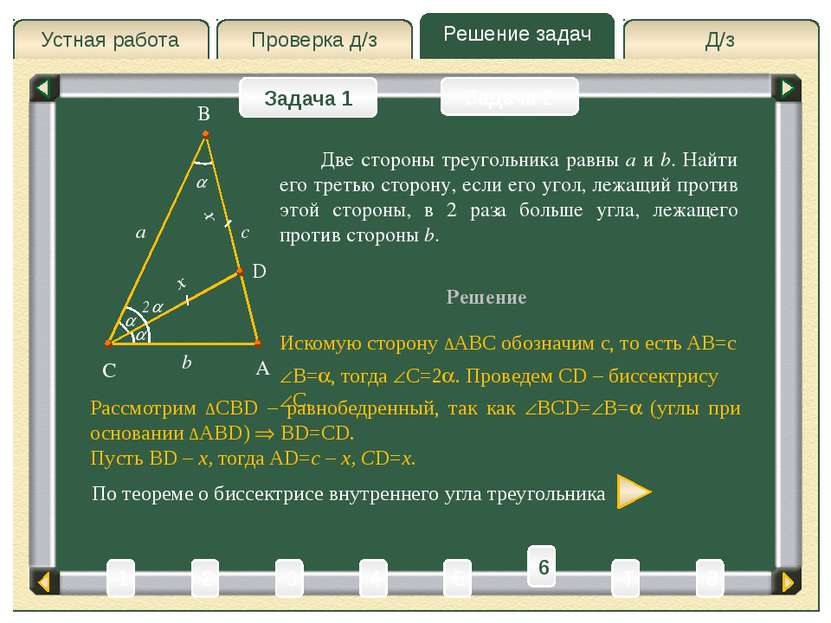
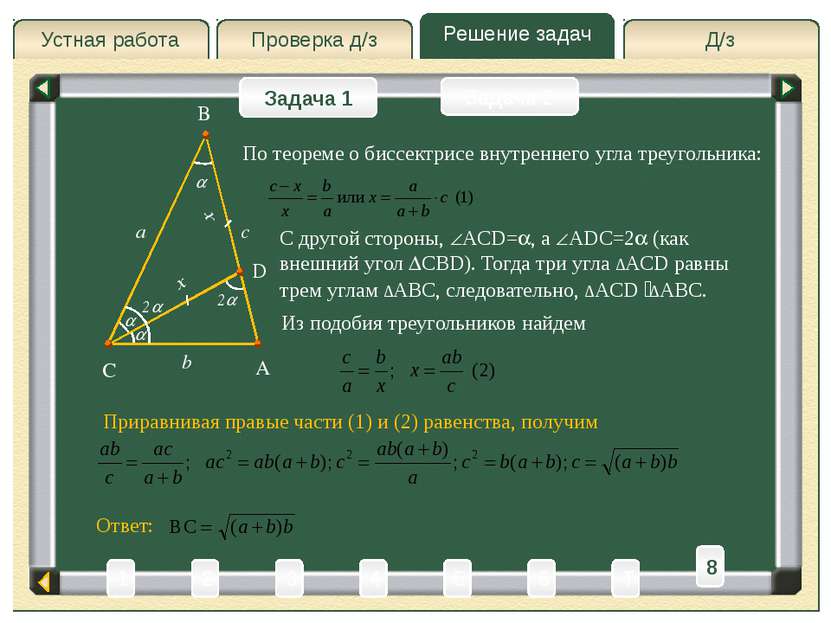
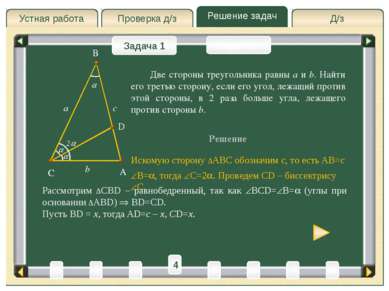
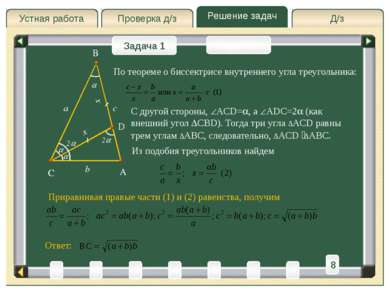
Д/з Проверка д/з Решение задач Устная работа Проверка д/з Задача 1 Задача 2 Решение A C B a b Искомую сторону ∆ABC обозначим c, то есть AB=c Две стороны треугольника равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b. c B= , тогда C=2 . Проведем CD – биссектрису C. 2 D Рассмотрим ∆CBD – равнобедренный, так как BCD= B= (углы при основании ∆ABD) BD=CD. Пусть BD – x, тогда AD=c – x, CD=x. x x 3 4 2 6 1 8 T 5
Cлайд 8
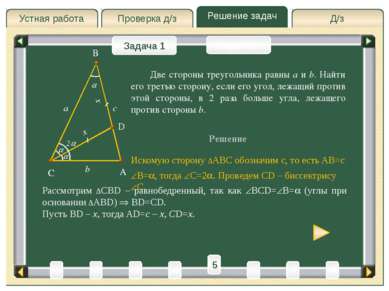
Д/з Проверка д/з Решение задач Устная работа Проверка д/з Задача 1 Задача 2 Решение A C B a b Искомую сторону ∆ABC обозначим c, то есть AB=c c B= , тогда C=2 . Проведем CD – биссектрису C. Две стороны треугольника равны a и b. Найти его третью сторону, если его угол, лежащий против этой стороны, в 2 раза больше угла, лежащего против стороны b. 3 4 5 6 1 8 T 2
Cлайд 9
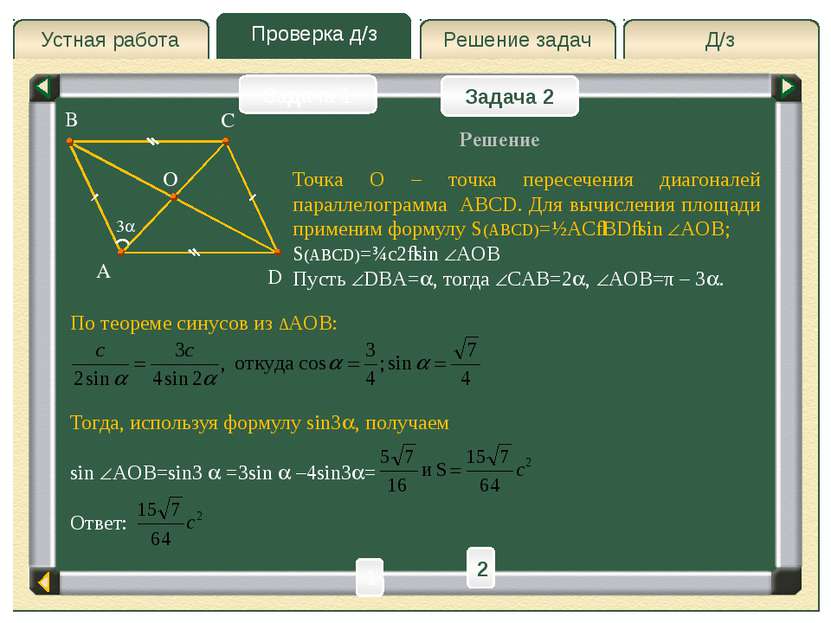
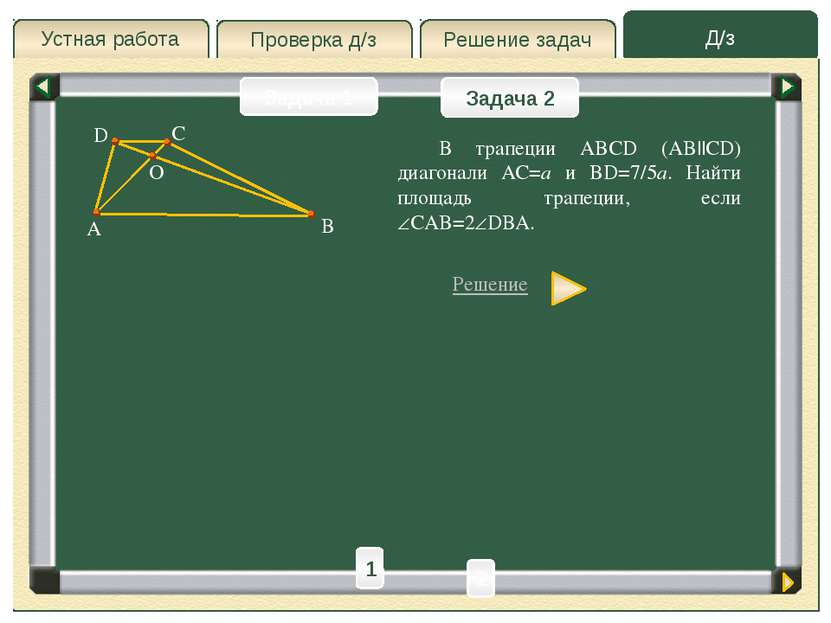
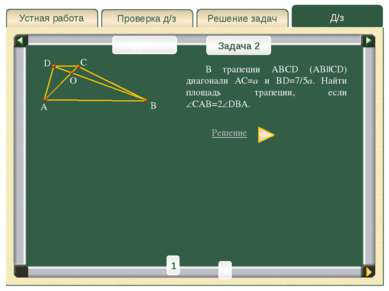
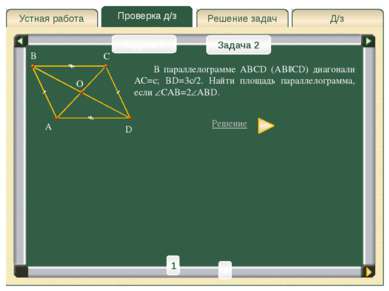
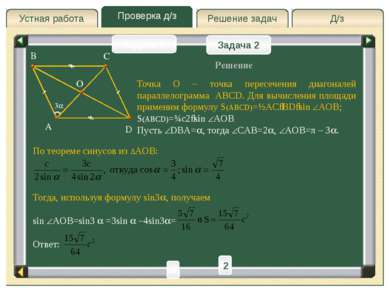
Проверка д/з Д/з Решение задач Устная работа Проверка д/з Задача 2 Задача 2 Задача 1 A D B C О E Решение Пусть DBA= , тогда CAB=2 . BE=CD; CE=BD; CEA= DBA= – соответственные при DB||CE и AE секущая. Ответ: Через вершину C проведем CE||DB до пересечения ее с продолжением основания AB в точке E. 2 h – высота ACE и трапеции ABCD. Для ACE применим теорему синусов: 2 1
Cлайд 10
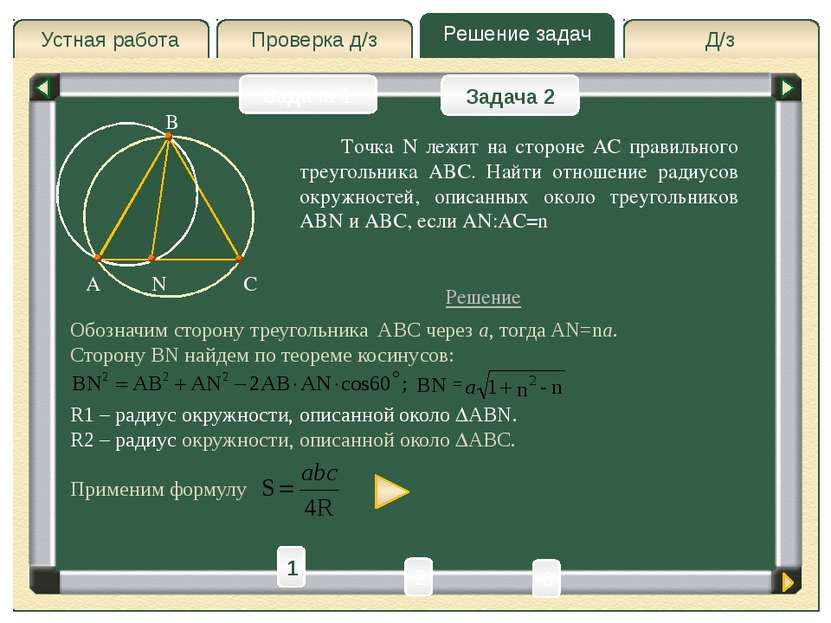
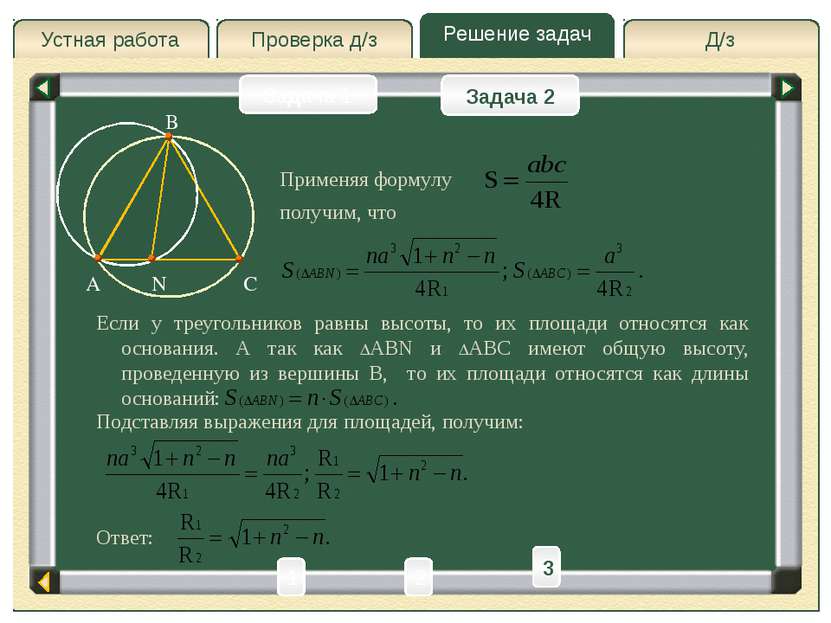
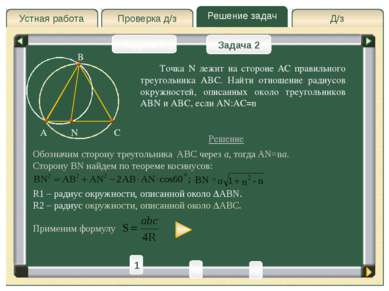
Д/з Проверка д/з Решение задач Устная работа Проверка д/з Задача 1 Задача 2 B A C N Применяя формулу получим, что Если у треугольников равны высоты, то их площади относятся как основания. А так как ABN и ABC имеют общую высоту, проведенную из вершины B, то их площади относятся как длины оснований: Подставляя выражения для площадей, получим: Ответ: 2 1 3
Cлайд 11
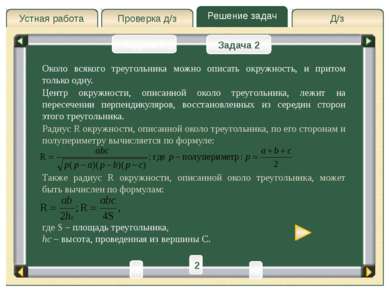
Д/з Проверка д/з Решение задач Устная работа Проверка д/з Около всякого треугольника можно описать окружность, и притом только одну. Задача 1 Задача 2 Центр окружности, описанной около треугольника, лежит на пересечении перпендикуляров, восстановленных из середин сторон этого треугольника. Радиус R окружности, описанной около треугольника, по его сторонам и полупериметру вычисляется по формуле: Также радиус R окружности, описанной около треугольника, может быть вычислен по формулам: где S – площадь треугольника, hc – высота, проведенная из вершины С. 3 2 1
Cлайд 12
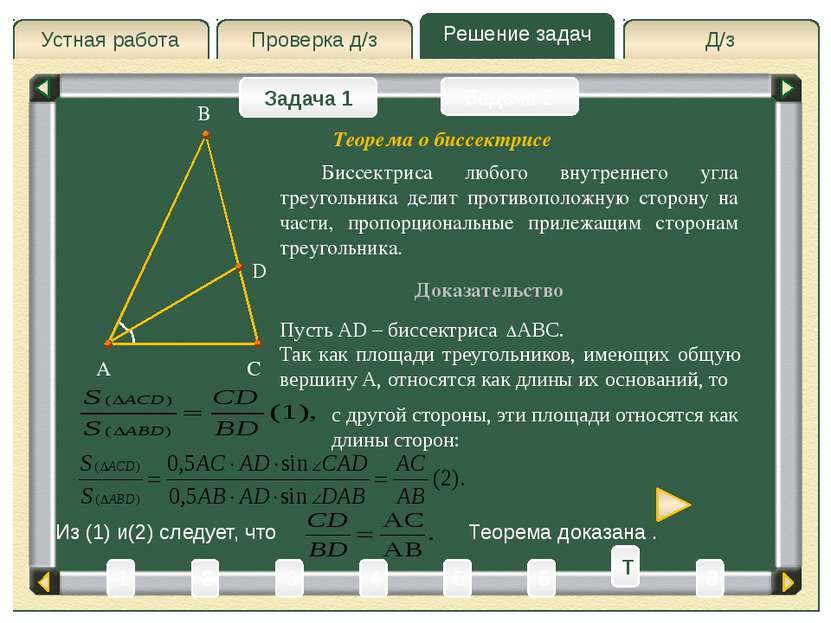
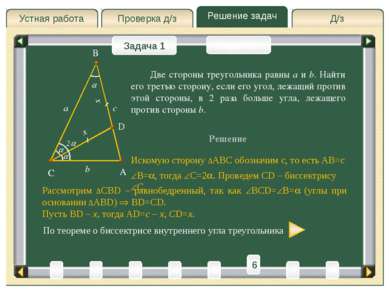
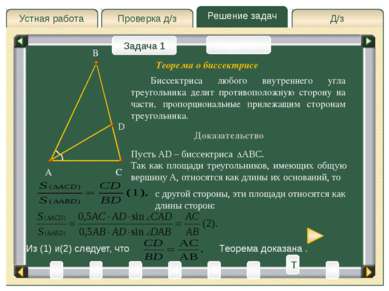
Д/з Проверка д/з Решение задач Устная работа Проверка д/з Задача 1 Задача 2 Доказательство A C B Пусть AD – биссектриса ABC. Так как площади треугольников, имеющих общую вершину A, относятся как длины их оснований, то Биссектриса любого внутреннего угла треугольника делит противоположную сторону на части, пропорциональные прилежащим сторонам треугольника. D Теорема о биссектрисе с другой стороны, эти площади относятся как длины сторон: Из (1) и(2) следует, что Теорема доказана . 3 4 5 2 6 1 8 T
Cлайд 13
Устная работа Д/з Решение задач Проверка д/з Выход Спасибо за внимание
Cлайд 14
Cлайд 15
Cлайд 16
Cлайд 17
Cлайд 18
Cлайд 19
Cлайд 20
Cлайд 21
Cлайд 22
Cлайд 23
Cлайд 24
Cлайд 25
Cлайд 26
Cлайд 27
