X
Код презентации скопируйте его
Расстояние между прямыми в пространстве
Скачать эту презентацию
Презентация на тему Расстояние между прямыми в пространстве
Скачать эту презентациюCлайд 1
РАССТОЯНИЕ МЕЖДУ ПРЯМЫМИ В ПРОСТРАНСТВЕ Расстоянием между двумя непересекающимися прямыми в пространстве называется длина общего перпендикуляра, проведенного к этим прямым.
Cлайд 2
Первый способ сводится к нахождению расстояния от точки до плоскости Идея заключается в построении: а) двух параллельных плоскостей, каждая из которых проходит через одну из скрещивающихся прямых, параллельно другой скрещивающейся прямой. Расстояние между этими плоскостями будет искомым. б) в построении плоскости, проходящей через одну из скрещивающихся прямых, параллельно другой. Расстояние от любой точки второй прямой до построенной плоскости будет искомым.
Cлайд 3
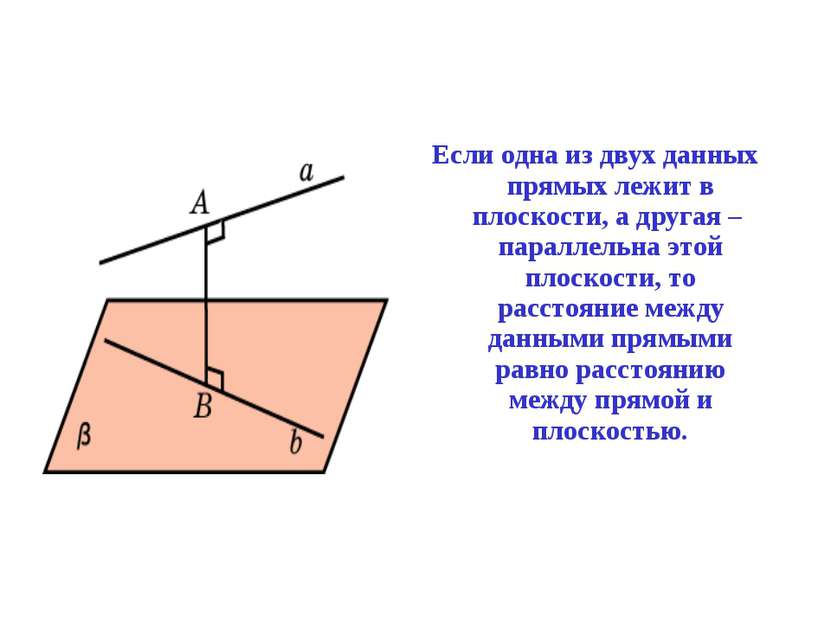
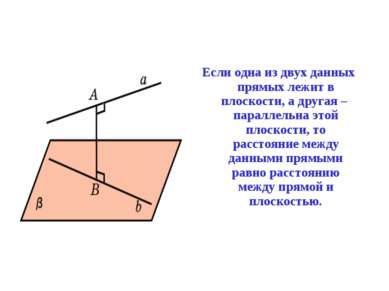Если одна из двух данных прямых лежит в плоскости, а другая – параллельна этой плоскости, то расстояние между данными прямыми равно расстоянию между прямой и плоскостью.
Cлайд 4
Второй способ нахождения расстояния между скрещивающимися прямыми основан на методе ортогонального проектирования. Расстояние между скрещивающимися прямыми от точки, являющейся проекцией одной из данных прямых на перпендикулярную ей плоскость до проекции другой прямой на эту плоскость. Угол между второй прямой и указанной ей проекцией дополняет до 90° угол между данными скрещивающимися прямыми.
Cлайд 5
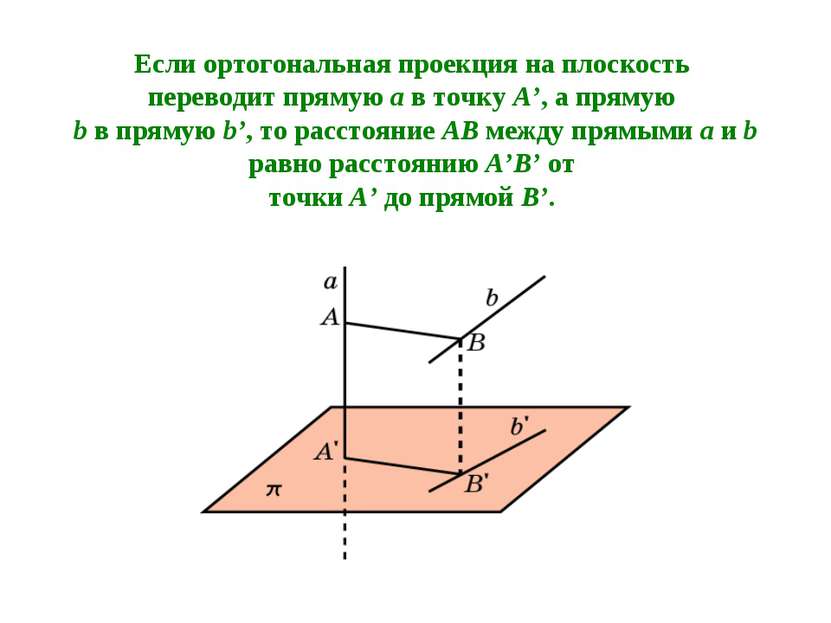
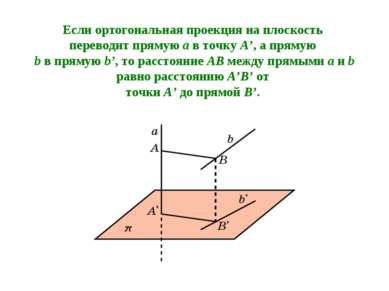Если ортогональная проекция на плоскость переводит прямую a в точку A’, а прямую b в прямую b’, то расстояние AB между прямыми a и b равно расстоянию A’B’ от точки A’ до прямой B’.
Cлайд 6
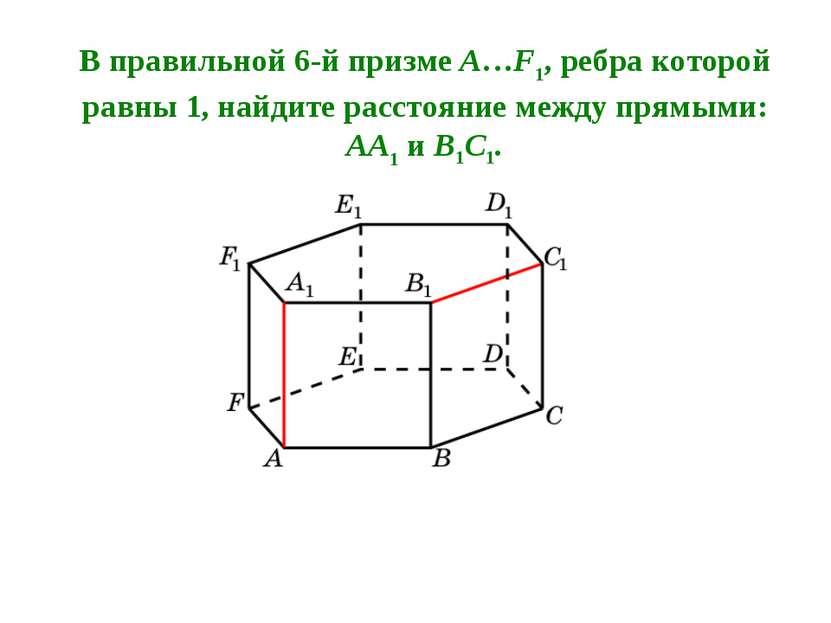
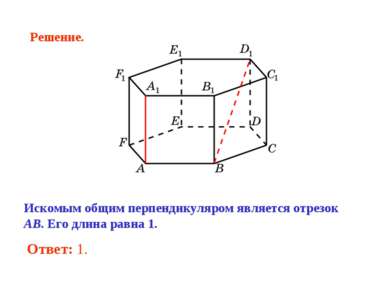
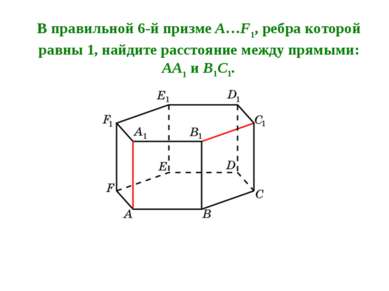В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и B1C1.
Cлайд 7
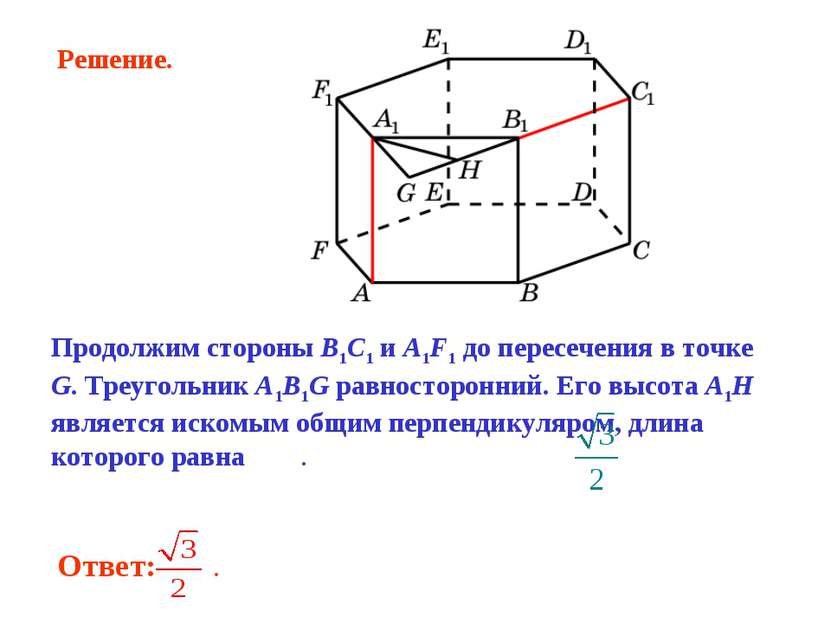
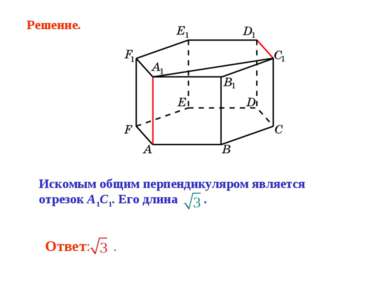
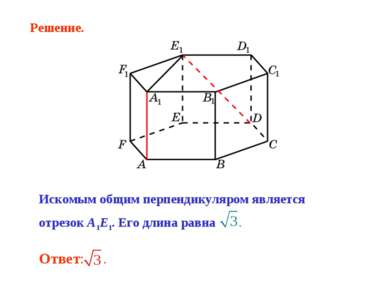
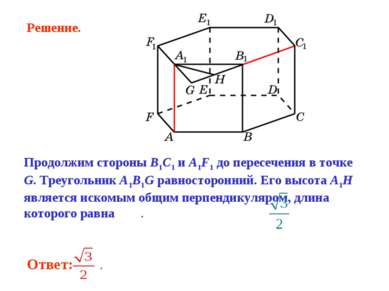Продолжим стороны B1C1 и A1F1 до пересечения в точке G. Треугольник A1B1G равносторонний. Его высота A1H является искомым общим перпендикуляром, длина которого равна . Решение.
Cлайд 8
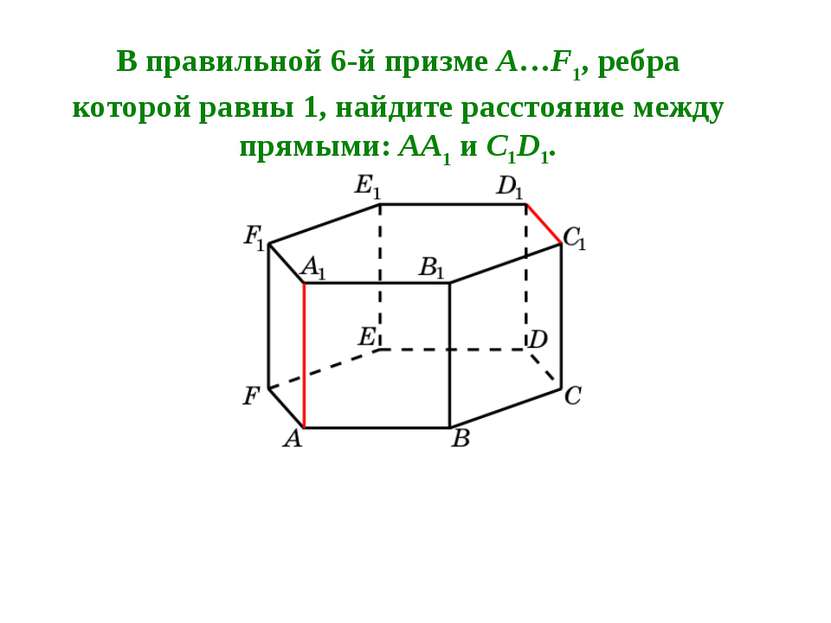
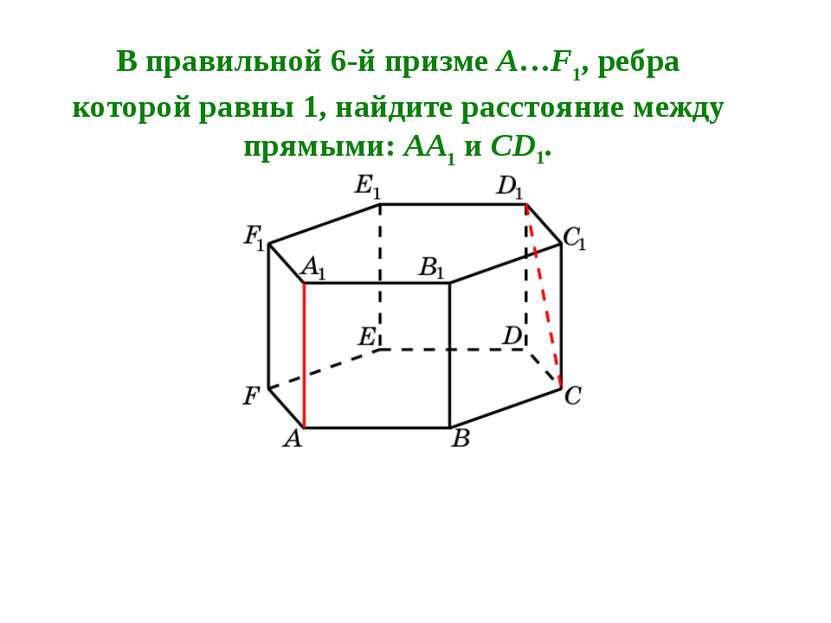
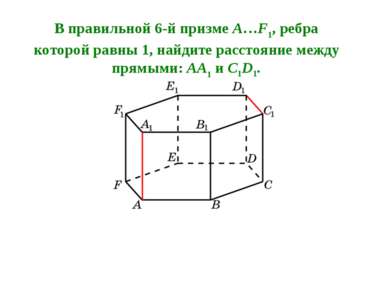В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и C1D1.
Cлайд 9
Искомым общим перпендикуляром является отрезок A1C1. Его длина . Решение.
Cлайд 10
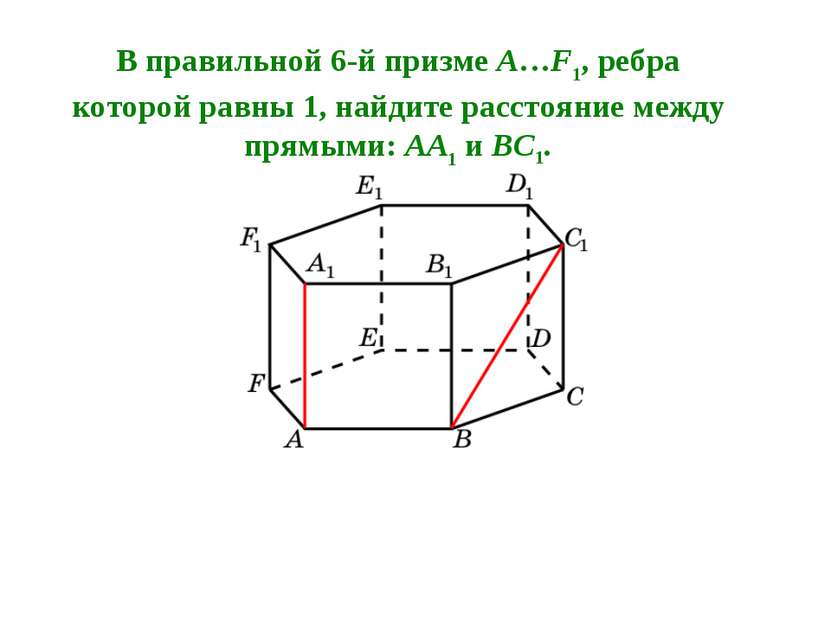
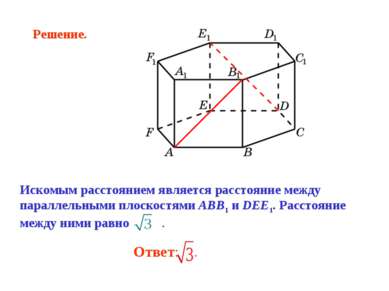
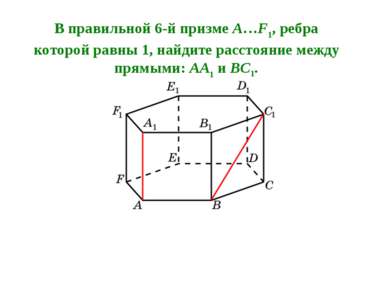В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BC1.
Cлайд 11
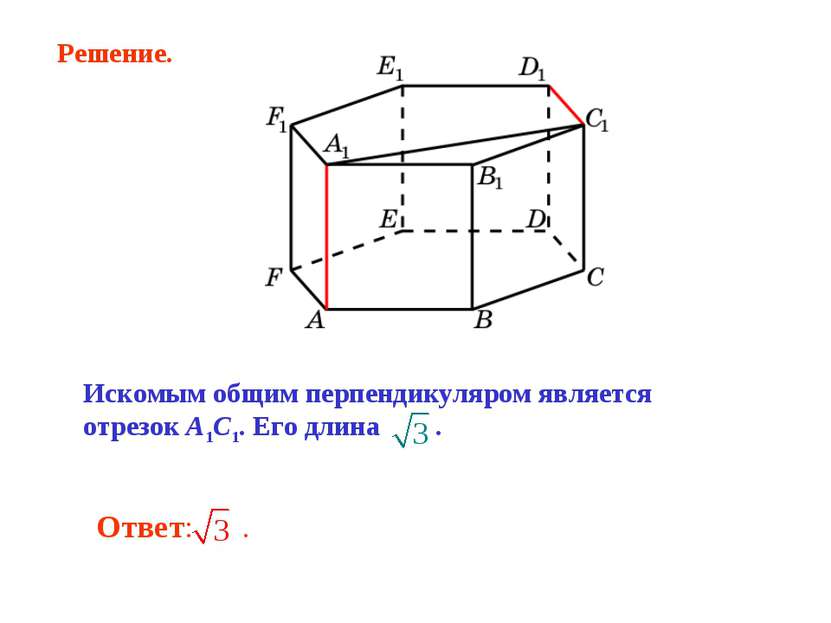
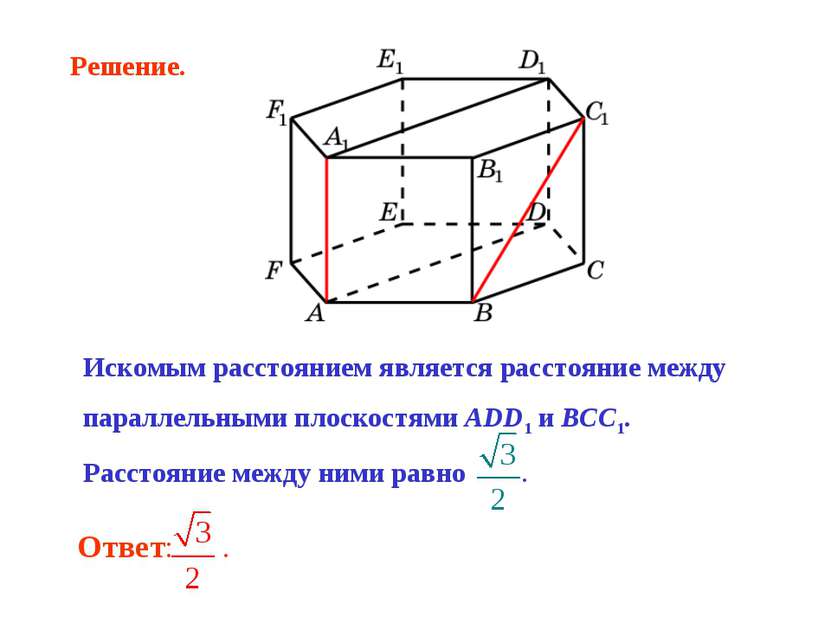
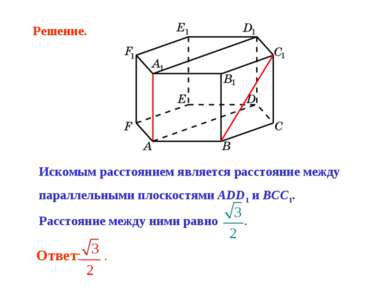Искомым расстоянием является расстояние между параллельными плоскостями ADD1 и BCC1. Расстояние между ними равно . Решение.
Cлайд 12
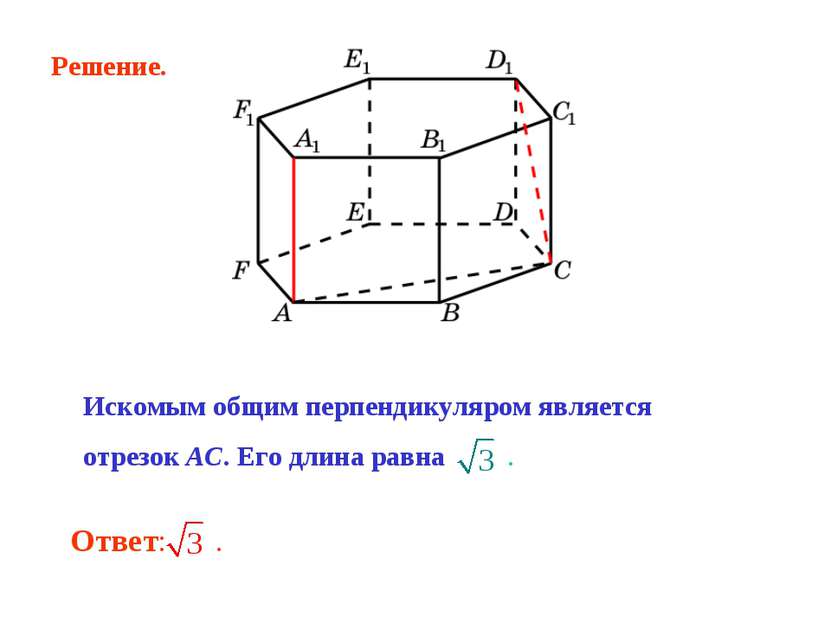
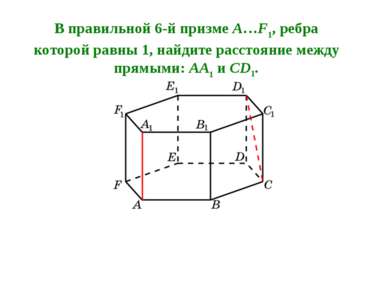В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CD1.
Cлайд 13
Искомым общим перпендикуляром является отрезок AC. Его длина равна . Решение.
Cлайд 14
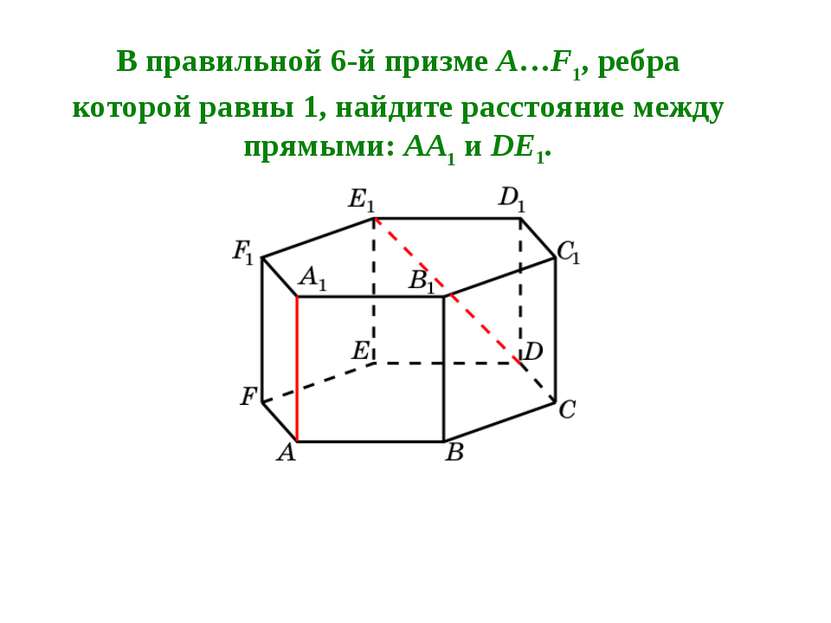
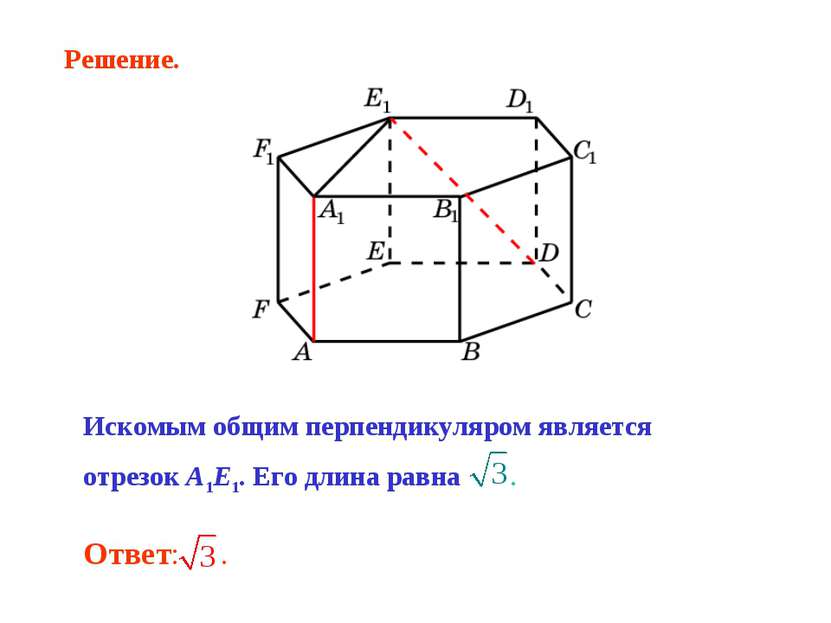
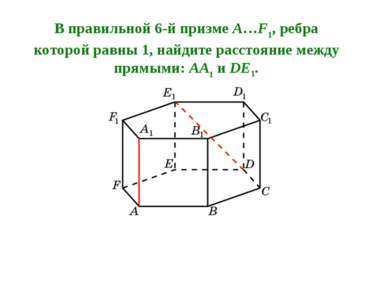В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и DE1.
Cлайд 15
Искомым общим перпендикуляром является отрезок A1E1. Его длина равна . Решение.
Cлайд 16
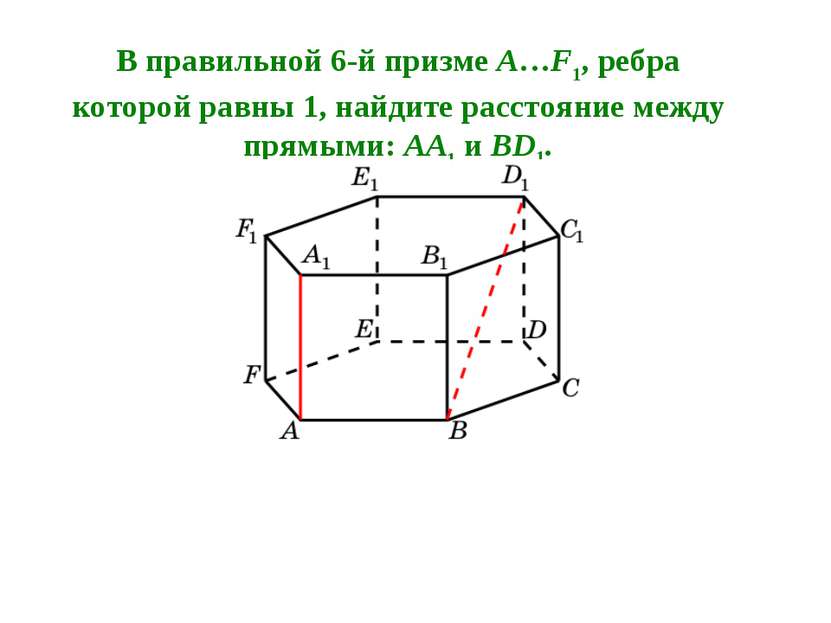
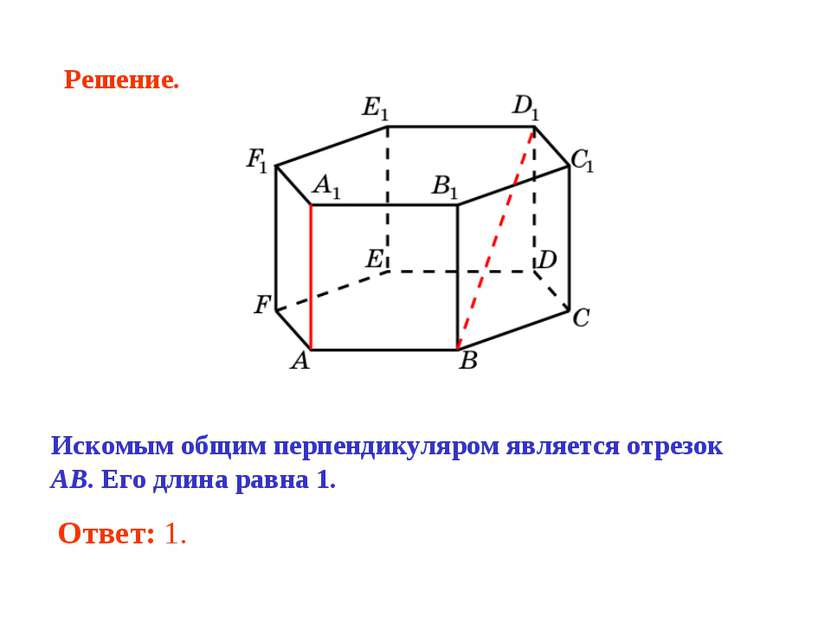
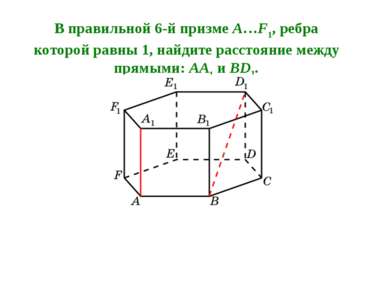В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BD1.
Cлайд 17
Решение.
Cлайд 18
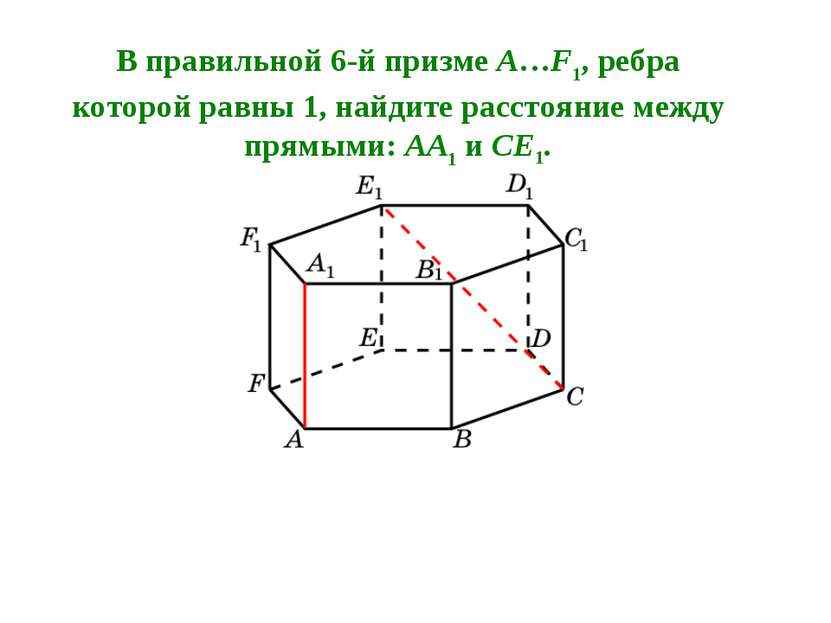
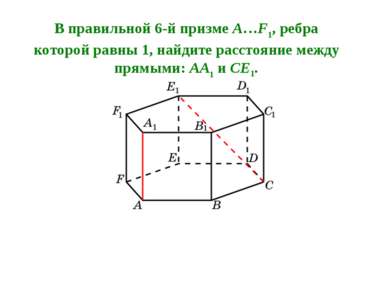В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CE1.
Cлайд 19
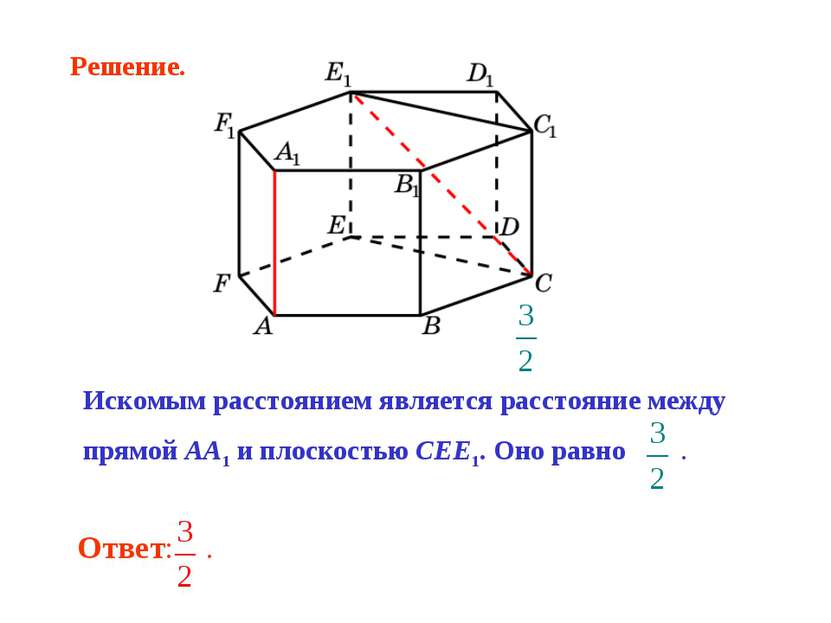
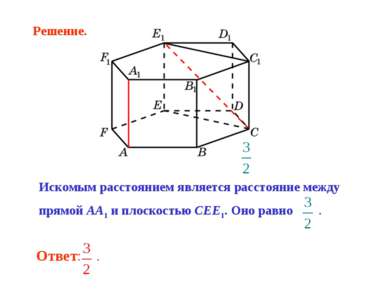Искомым расстоянием является расстояние между прямой AA1 и плоскостью CEE1. Оно равно . Решение.
Cлайд 20
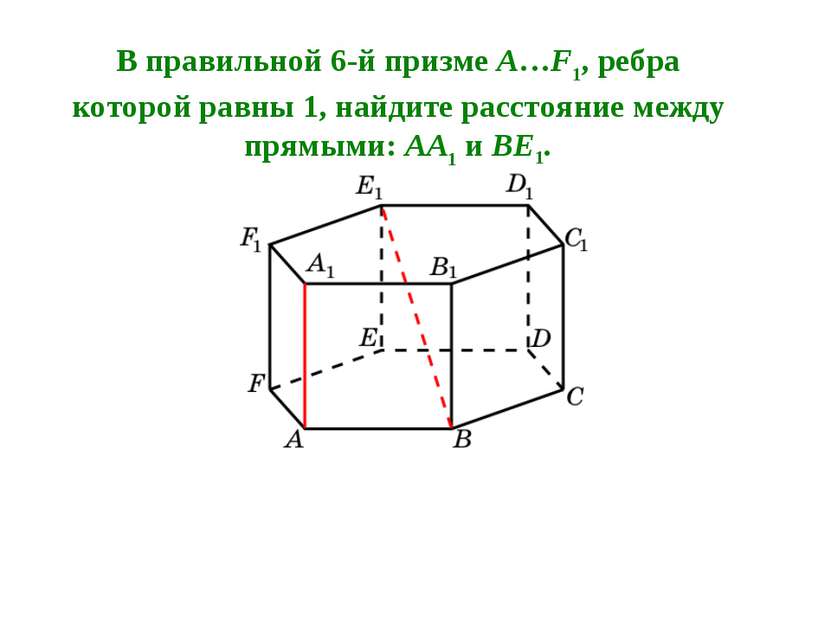
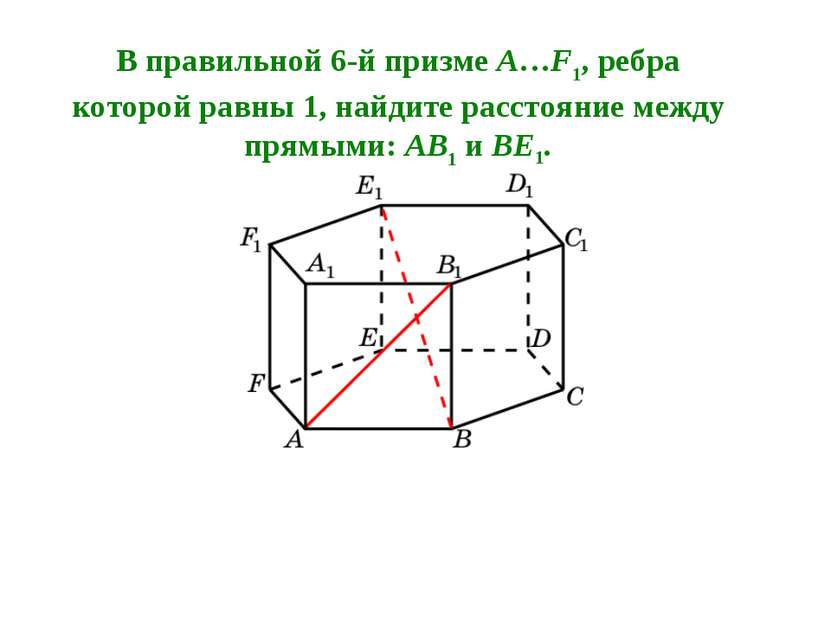
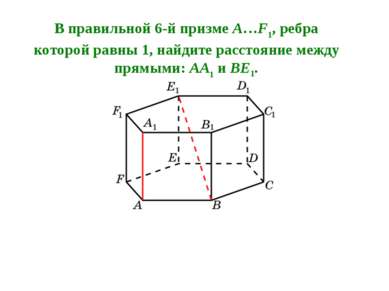В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и BE1.
Cлайд 21
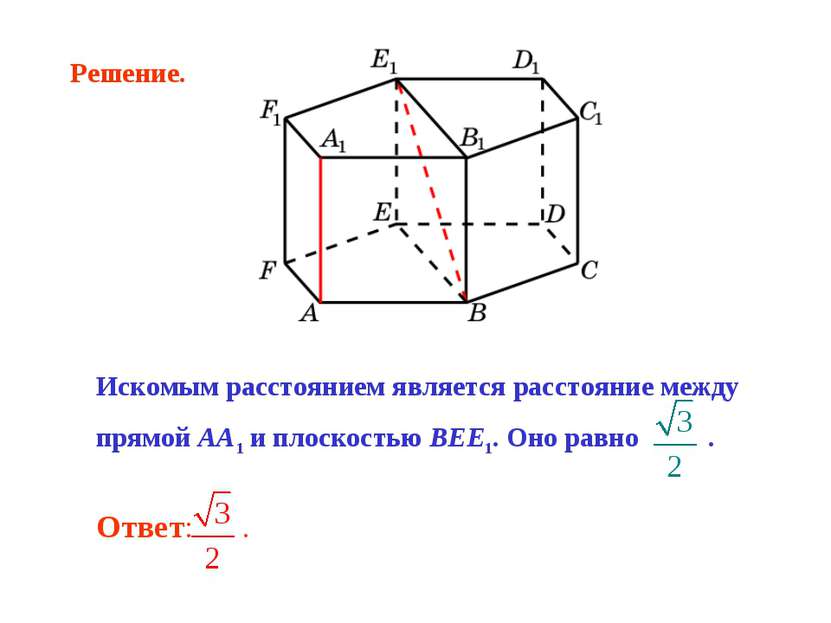
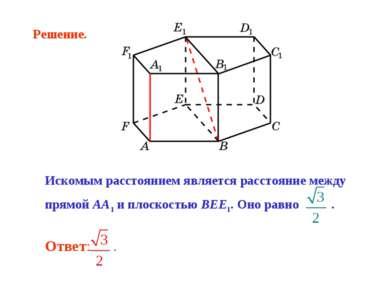Искомым расстоянием является расстояние между прямой AA1 и плоскостью BEE1. Оно равно . Решение.
Cлайд 22
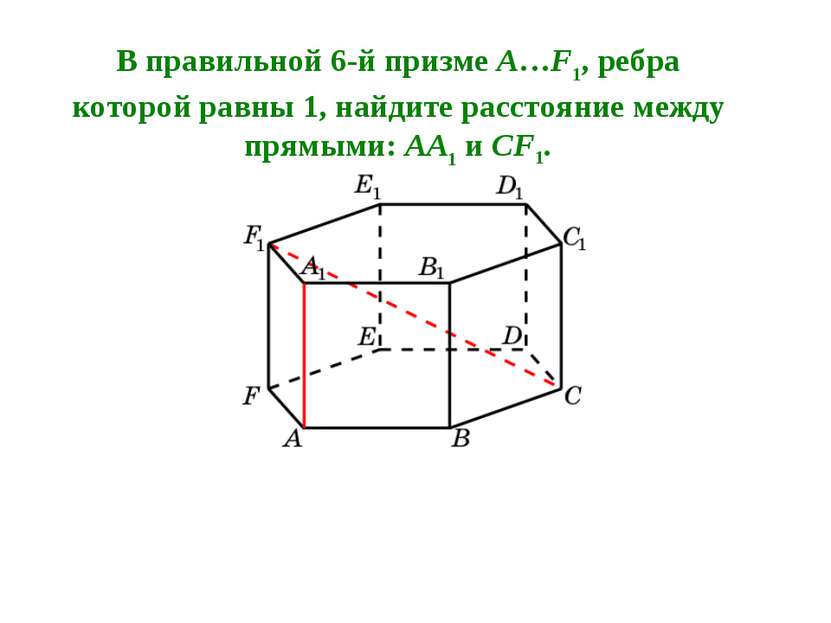
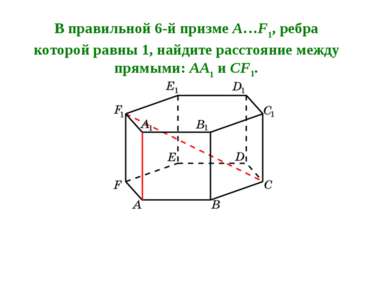В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AA1 и CF1.
Cлайд 23
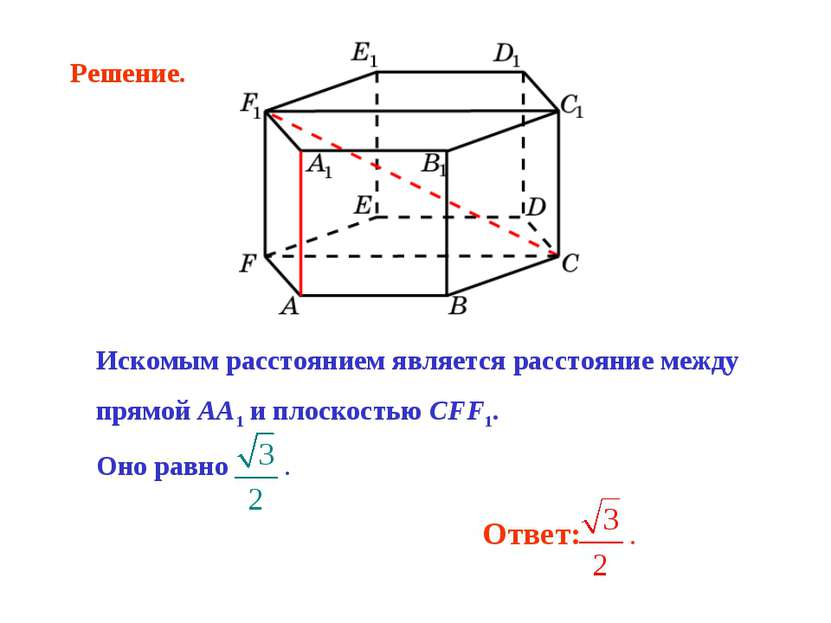
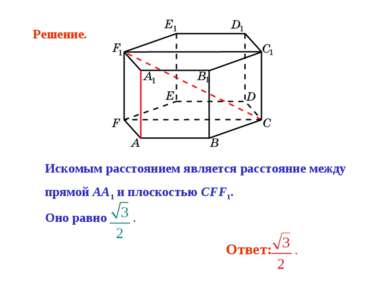Искомым расстоянием является расстояние между прямой AA1 и плоскостью CFF1. Оно равно . Решение.
Cлайд 24
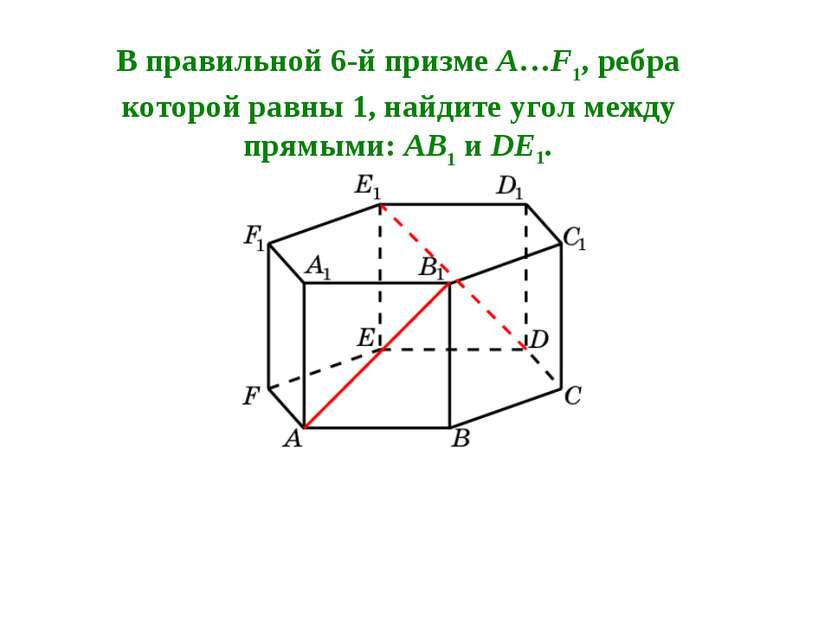
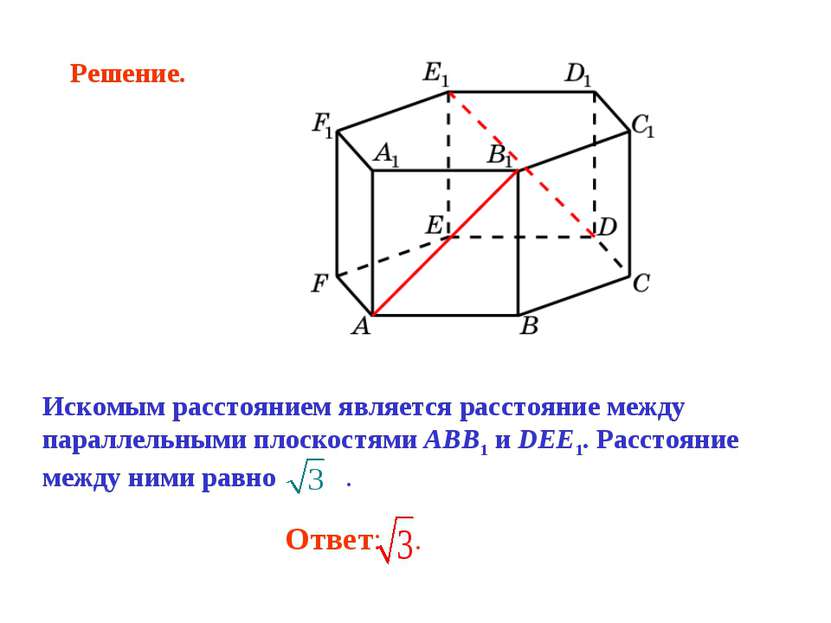
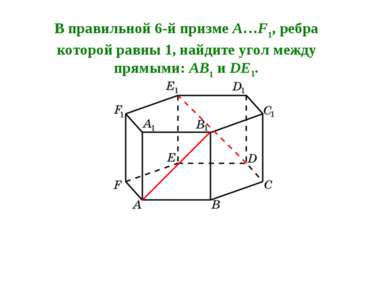В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и DE1.
Cлайд 25
Решение.
Cлайд 26
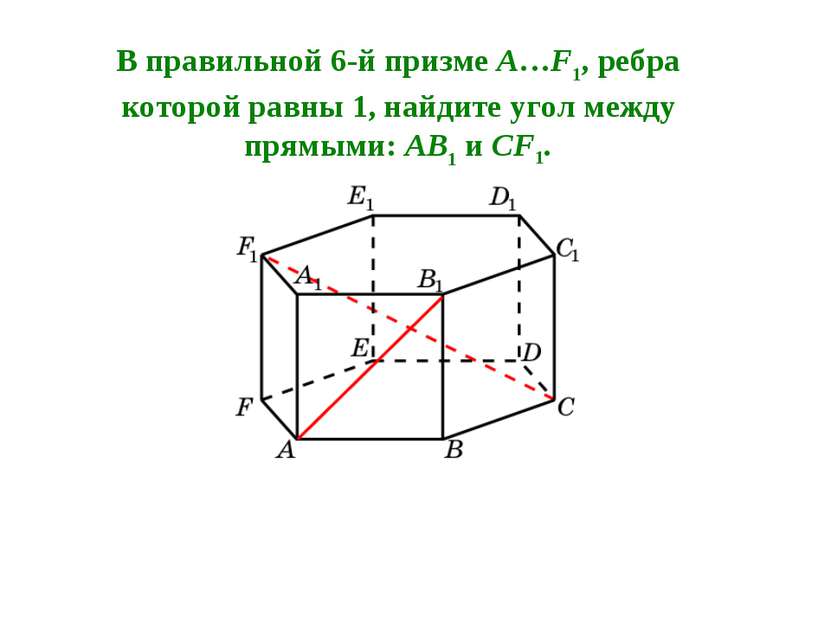
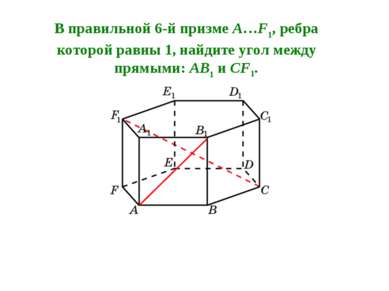В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и CF1.
Cлайд 27
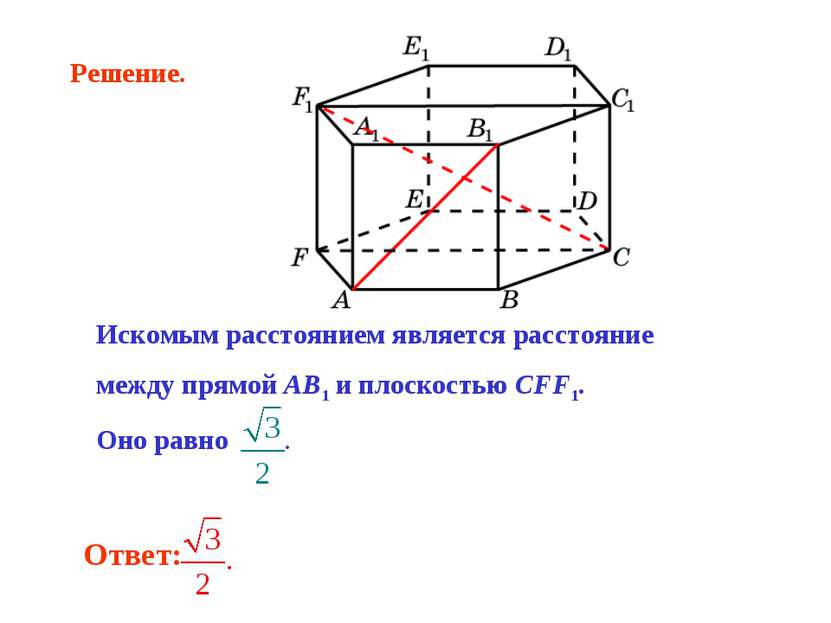
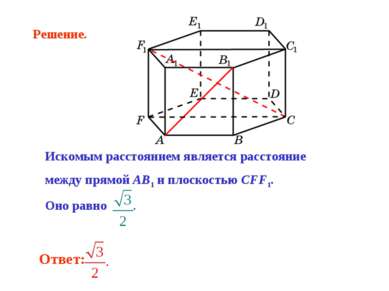Искомым расстоянием является расстояние между прямой AB1 и плоскостью CFF1. Оно равно . Решение.
Cлайд 28
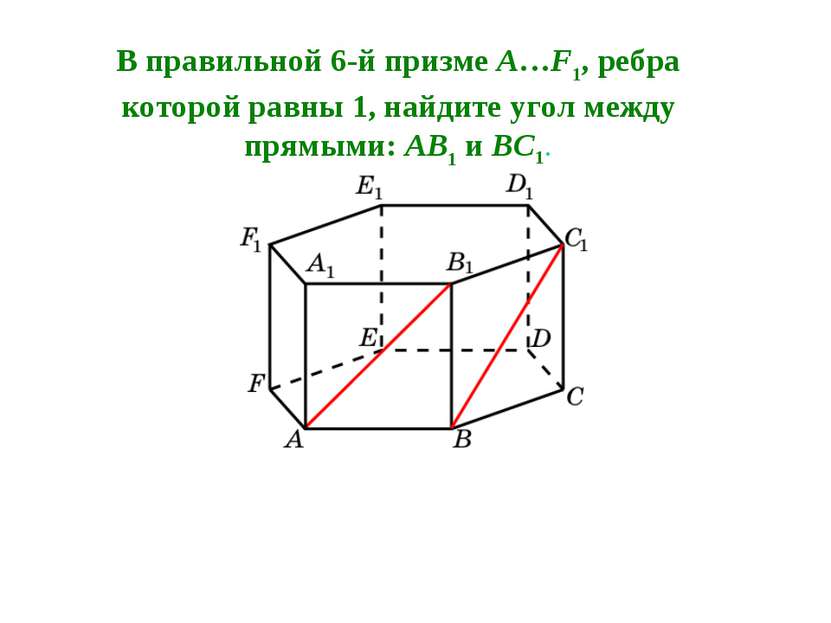
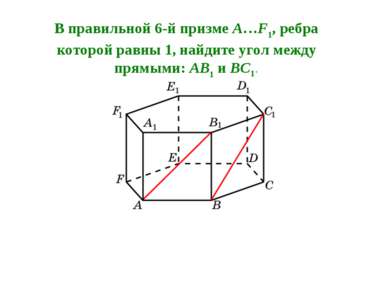В правильной 6-й призме A…F1, ребра которой равны 1, найдите угол между прямыми: AB1 и BC1.
Cлайд 29
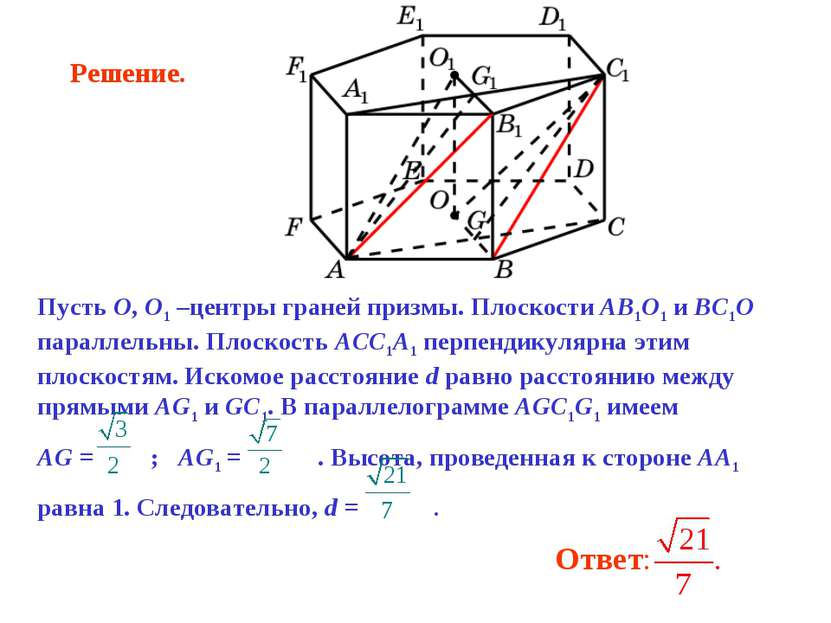
Пусть O, O1 –центры граней призмы. Плоскости AB1O1 и BC1O параллельны. Плоскость ACC1A1 перпендикулярна этим плоскостям. Искомое расстояние d равно расстоянию между прямыми AG1 и GC1. В параллелограмме AGC1G1 имеем AG = ; AG1 = . Высота, проведенная к стороне AA1 равна 1. Следовательно, d = . Решение.
Cлайд 30
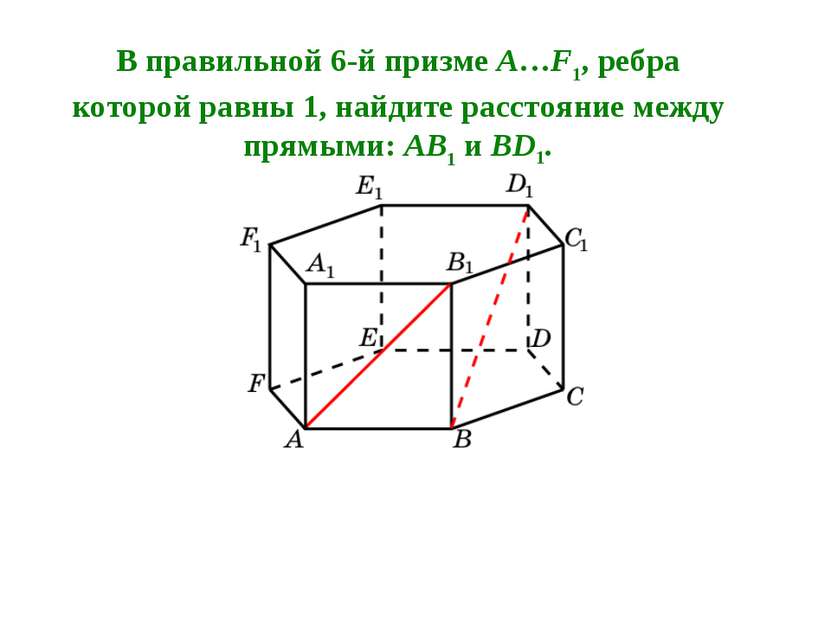
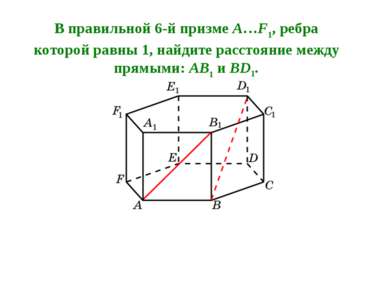В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB1 и BD1.
Cлайд 31
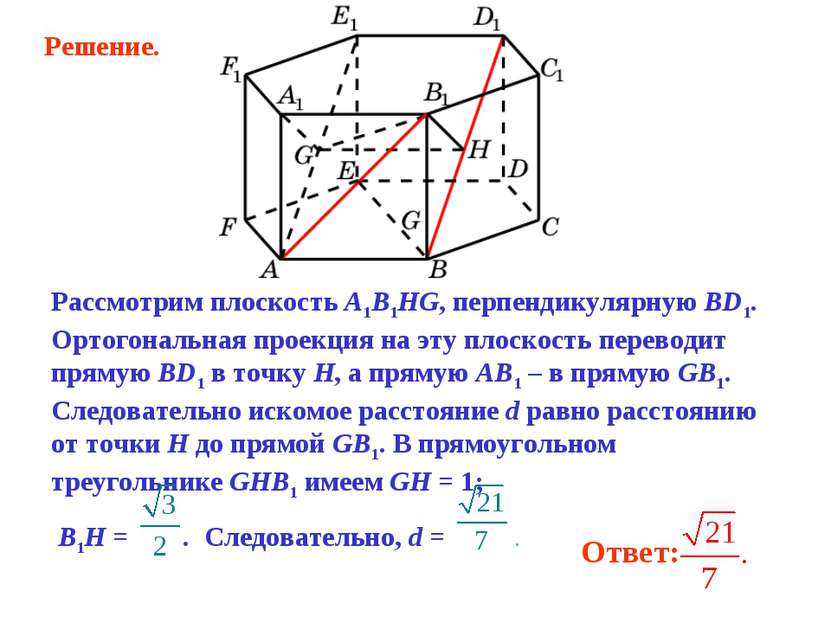
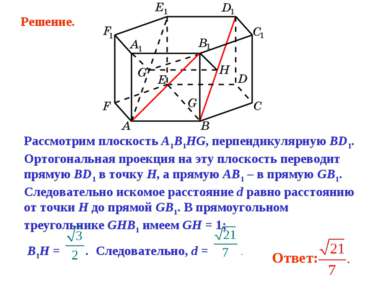Рассмотрим плоскость A1B1HG, перпендикулярную BD1. Ортогональная проекция на эту плоскость переводит прямую BD1 в точку H, а прямую AB1 – в прямую GB1. Следовательно искомое расстояние d равно расстоянию от точки H до прямой GB1. В прямоугольном треугольнике GHB1 имеем GH = 1; B1H = . Следовательно, d = . Решение.
Cлайд 32
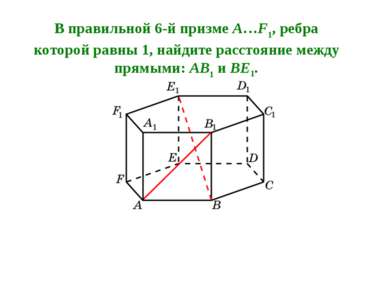В правильной 6-й призме A…F1, ребра которой равны 1, найдите расстояние между прямыми: AB1 и BE1.
Cлайд 33
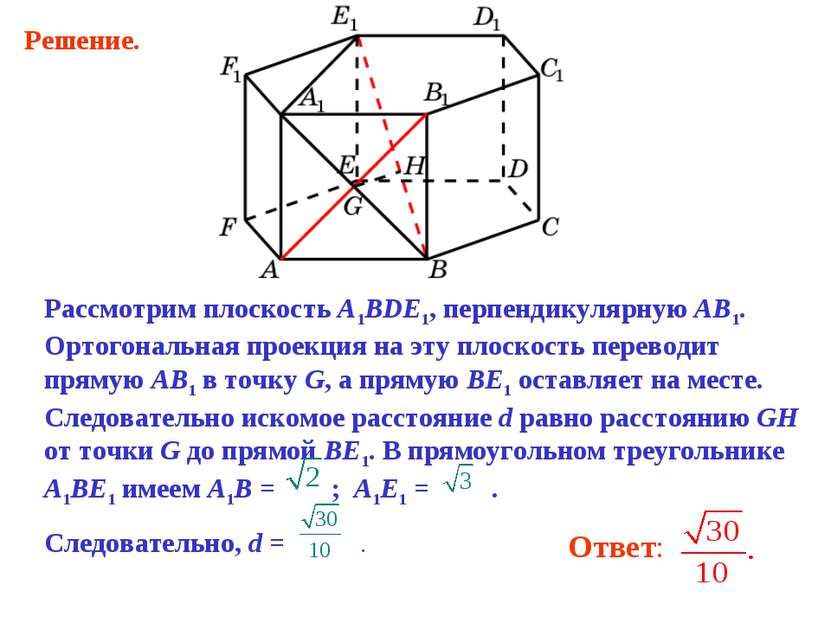
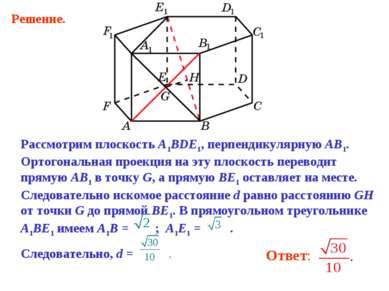Рассмотрим плоскость A1BDE1, перпендикулярную AB1. Ортогональная проекция на эту плоскость переводит прямую AB1 в точку G, а прямую BE1 оставляет на месте. Следовательно искомое расстояние d равно расстоянию GH от точки G до прямой BE1. В прямоугольном треугольнике A1BE1 имеем A1B = ; A1E1 = . Следовательно, d = . Решение.
