X
Код презентации скопируйте его
Полуправильные и звездчатые многогранники. Кристаллы
Скачать эту презентацию
Презентация на тему Полуправильные и звездчатые многогранники. Кристаллы
Скачать эту презентациюCлайд 1
Полуправильные и звездчатые многогранники. Кристаллы. Бурак Анастасия 10 В
Cлайд 2
Полуправильные многогранники Архимедовы тела Архимедовы тела — выпуклые многогранники, обладающие двумя свойствами: Все грани являются правильными многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник); Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности, все многогранные углы при вершинах конгруэнтны.
Cлайд 3
Полуправильные многогранники Каталановы тела Двойственные архимедовым телам, так называемые Каталановы тела, имеют конгруэнтные грани, равные двугранные углы и правильные многогранные углы. Каталановы тела тоже иногда называют полуправильными многогранниками. В этом случае полуправильными многогранниками считается совокупность архимедовых и каталановых тел. Архимедовы тела являются полуправильными многогранниками в том смысле, что их грани — правильные многоугольники, но они не одинаковы, а каталановы — в том смысле, что их грани одинаковы, но не являются правильными многоугольниками; при этом для тех и других сохраняется условие одного из типов пространственной симметрии: тетраэдрического, октаэдрического или икосаэдрического. То есть, полуправильными в этом случае называются тела, у которых отсутствует только одно из первых двух из следующих свойств правильных тел: Все грани являются правильными многоугольниками; Все грани одинаковы; Тело относится к одному из трёх существующих типов пространственной симметрии.
Cлайд 4
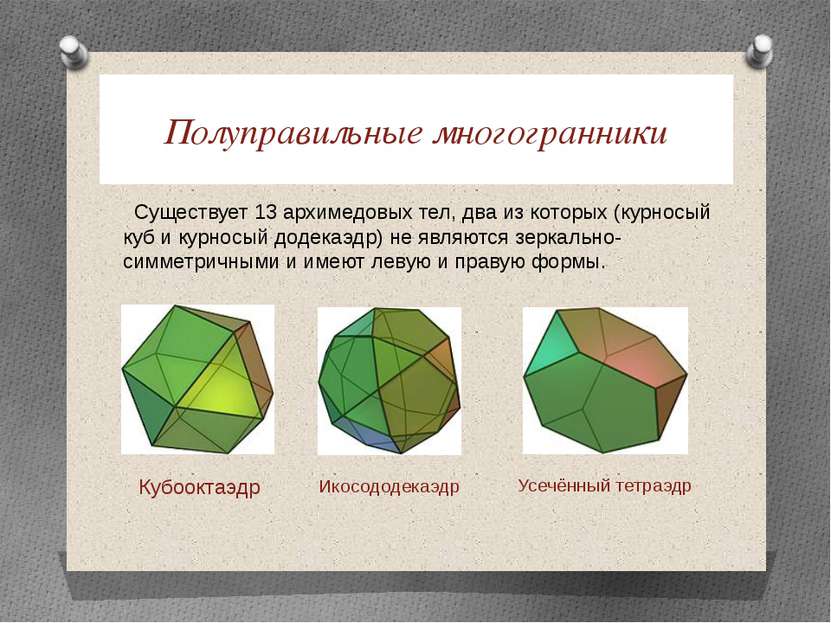
Полуправильные многогранники Существует 13 архимедовых тел, два из которых (курносый куб и курносый додекаэдр) не являются зеркально-симметричными и имеют левую и правую формы. Кубооктаэдр Икосододекаэдр Усечённый тетраэдр
Cлайд 5
Полуправильные многогранники Усечённый октаэдр Усечённый икосаэдр Усечённый куб Усечённый додекаэдр Ромбокубооктаэдр Ромбоикосододекаэдр
Cлайд 6
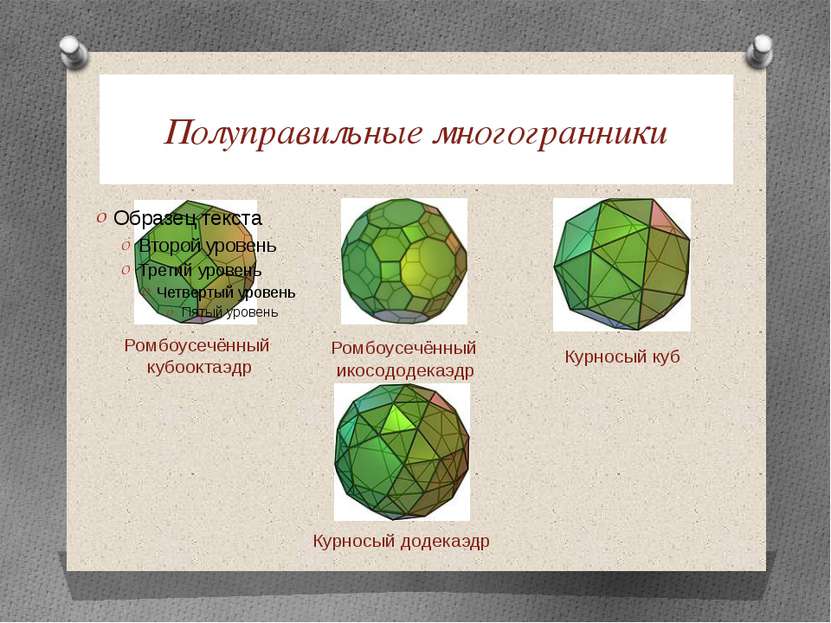
Полуправильные многогранники Ромбоусечённый кубооктаэдр Ромбоусечённый икосододекаэдр Курносый куб Курносый додекаэдр
Cлайд 7
Звездчатые многогранники Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами. Существует только одна звёздчатая форма октаэдра.
Cлайд 8
Звездчатые многогранники Додекаэдр имеет 3 звёздчатые формы: малый звёздчатый додекаэдр, большой додекаэдр, большой звёздчатый додекаэдр
Cлайд 9
Звездчатые многогранники Икосаэдр имеет 59 звёздчатых форм
Cлайд 10
Звездчатые многогранники Кубооктаэдр имеет 4 звёздчатые формы
Cлайд 11
Звездчатые многогранники Икосододекаэдр имеет множество звёздчатых форм, первая из которых есть соединение икосаэдра и додекаэдра
Cлайд 12
Кристаллы Кристаллы — это твёрдые вещества, имеющие естественную внешнюю форму правильных симметричных многогранников, основанную на их внутренней структуре, то есть на одном из нескольких определённых регулярных расположений составляющих вещество частиц (атомов, молекул, ионов).
Cлайд 13
Кристаллы Виды кристаллов Следует разделить идеальный и реальный кристалл. Идеальный кристалл Является, по сути, математическим объектом, имеющим полную, свойственную ему симметрию, идеализированно ровные гладкие грани. Реальный кристалл Всегда содержит различные дефекты внутренней структуры решетки, искажения и неровности на гранях и имеет пониженную симметрию многогранника вследствие специфики условий роста, неоднородности питающей среды, повреждений и деформаций. Реальный кристалл не обязательно обладает кристаллографическими гранями и правильной формой, но у него сохраняется главное свойство — закономерное положение атомов в кристаллической решётке.
Cлайд 14
Кристаллы
