X
Код презентации скопируйте его
Обработка данных статистических наблюдений
Скачать эту презентацию
![Рассчитываем расстояния между объектами*: d = [ (2 – 4)2 + (8 – 10)2 ]1/2 = 8...](https://bigslide.ru/images/51/50560/831/img35.jpg "Рассчитываем расстояния между объектами*: d = [ (2 – 4)2 + (8 – 10)2 ]1/2 = 8...")
Презентация на тему Обработка данных статистических наблюдений
Скачать эту презентациюCлайд 1
СТАТИСТИКА I (теория статистики) Часть 3. Обработка данных статистических наблюдений Кафедра Маркетинга и менеджмента (ММ) Бесплатные презентации http://prezentacija.biz/
Cлайд 2
Обработка данных статистических наблюдений включает: Статистическую сводку; Группировку; Ряды распределения; Кластерный анализ. Обработка данных статистических наблюдений
Cлайд 3
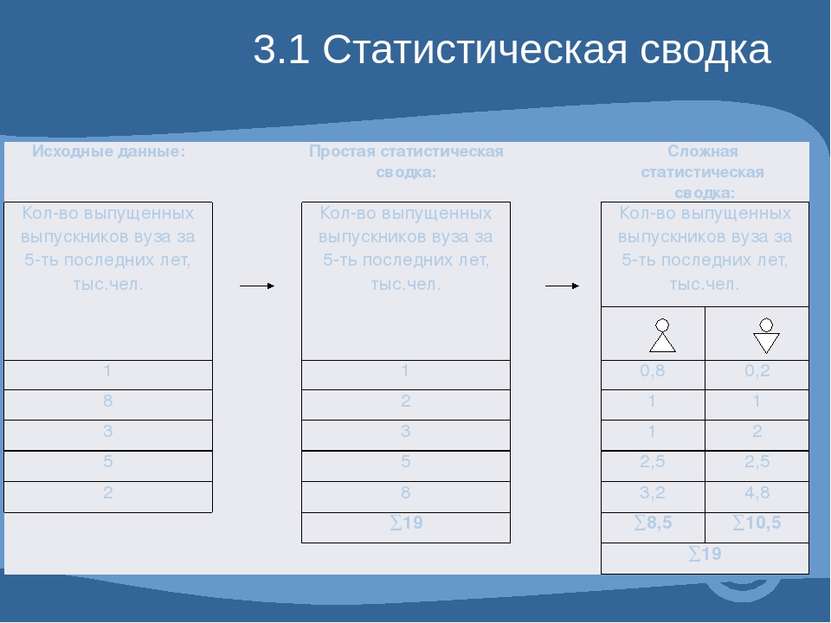
3.1 Статистическая сводка Исходные данные: Простая статистическая сводка: Сложная статистическая сводка: Кол-во выпущенных выпускников вуза за 5-ть последних лет, тыс.чел. Кол-во выпущенных выпускников вуза за 5-ть последних лет, тыс.чел. Кол-во выпущенных выпускников вуза за 5-ть последних лет, тыс.чел. 1 1 0,8 0,2 8 2 1 1 3 3 1 2 5 5 2,5 2,5 2 8 3,2 4,8 ∑19 ∑8,5 ∑10,5 ∑19
Cлайд 4
3.2 Группировка
Cлайд 5
3.2 Группировка Равные Неравные Специализированные Произвольные прогрессивно возрастающие и убывающие
Cлайд 6
3.2 Группировка
Cлайд 7
3.2 Группировка Метод группировки позволяет решить три задачи (разграничение условное, одна группировка может решить все задачи): Разделение всей совокупности на качественно однородные группы – типологические группировки; Характеристика структуры явления и структурных сдвигов – структурные группировки; Изучение взаимосвязей между отдельными признаками изучаемого явления – аналитические группировки.
Cлайд 8
Таблица 1. Типологическая группировка Группировка полиграфических предприятий одного из городов по формам собственности Тип собственности Число предприятий абсолютное в процентах к итогу Федеральная Акционерная Частная Итого 3 7 5 15 20 46,7 33,3 100,0
Cлайд 9
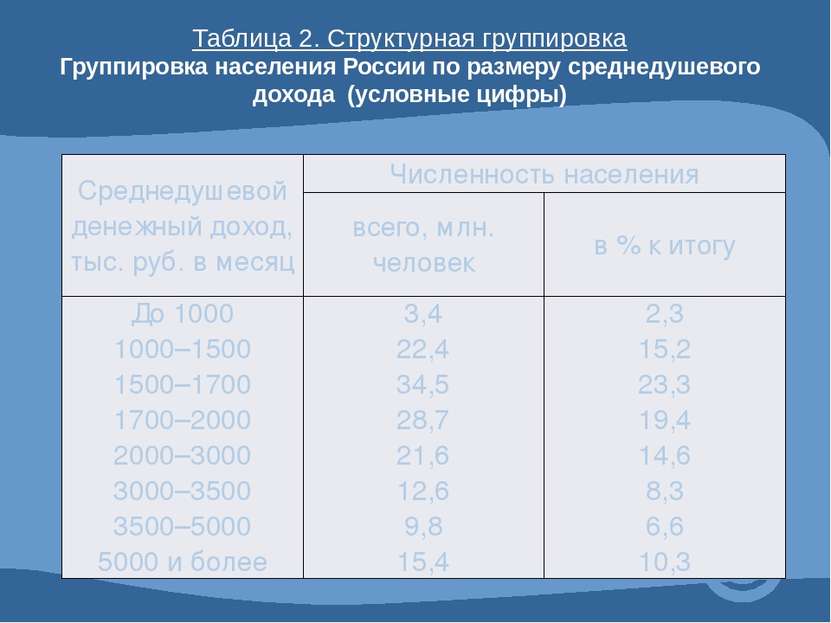
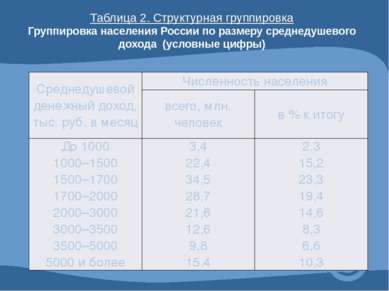Таблица 2. Структурная группировка Группировка населения России по размеру среднедушевого дохода (условные цифры) Среднедушевой денежный доход, тыс. руб. в месяц Численность населения всего, млн. человек в % к итогу До 1000 1000–1500 1500–1700 1700–2000 2000–3000 3000–3500 3500–5000 5000 и более 3,4 22,4 34,5 28,7 21,6 12,6 9,8 15,4 2,3 15,2 23,3 19,4 14,6 8,3 6,6 10,3
Cлайд 10
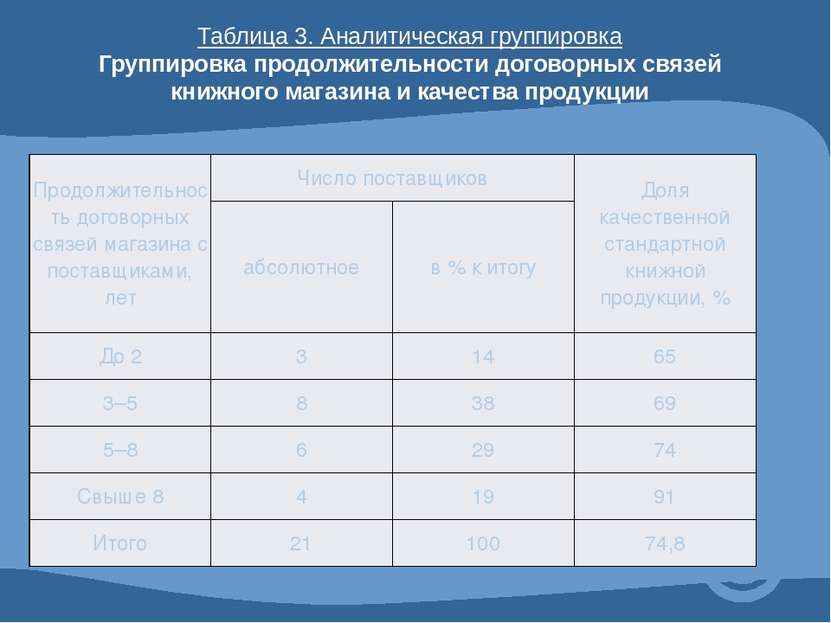
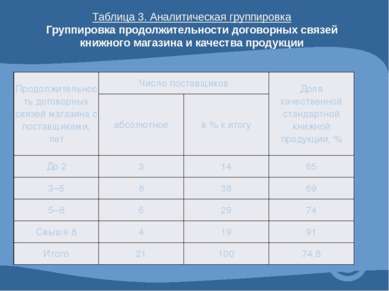Таблица 3. Аналитическая группировка Группировка продолжительности договорных связей книжного магазина и качества продукции Продолжительность договорных связей магазина с поставщиками, лет Число поставщиков Доля качественной стандартной книжной продукции, % абсолютное в % к итогу До 2 3 14 65 3–5 8 38 69 5–8 6 29 74 Свыше 8 4 19 91 Итого 21 100 74,8
Cлайд 11
3.2 Группировка
Cлайд 12
Методы определения числа групп, интервалов группировок После определения основания группировки следует решить вопрос о количестве групп, на которые надо разбить исследуемую совокупность. Число групп зависит от задач исследования, численности совокупности, степени вариации признака. После определения числа групп следует определить интервалы группировки. Интервал – это значения варьирующего признака, лежащие в определённых границах. Нижней границей интервала называется наименьшее значение признака в интервале, а верхней границей – наибольшее значение признака в нём. Величина (ширина) интервала представляет собой разность между верхней и нижней границами интервала.
Cлайд 13
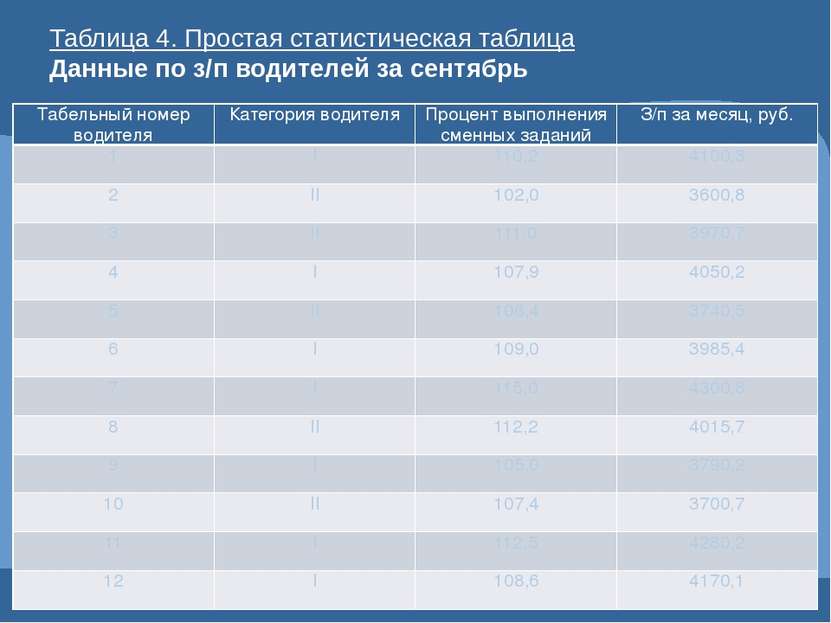
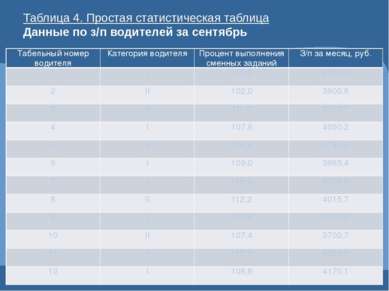Таблица 4. Простая статистическая таблица Данные по з/п водителей за сентябрь Табельный номер водителя Категория водителя Процент выполнения сменных заданий З/п за месяц, руб. 1 I 110,2 4100,3 2 II 102,0 3600,8 3 II 111,0 3970,7 4 I 107,9 4050,2 5 II 106,4 3740,5 6 I 109,0 3985,4 7 I 115,0 4300,8 8 II 112,2 4015,7 9 I 105,0 3790,2 10 II 107,4 3700,7 11 I 112,5 4280,2 12 I 108,6 4170,1
Cлайд 14
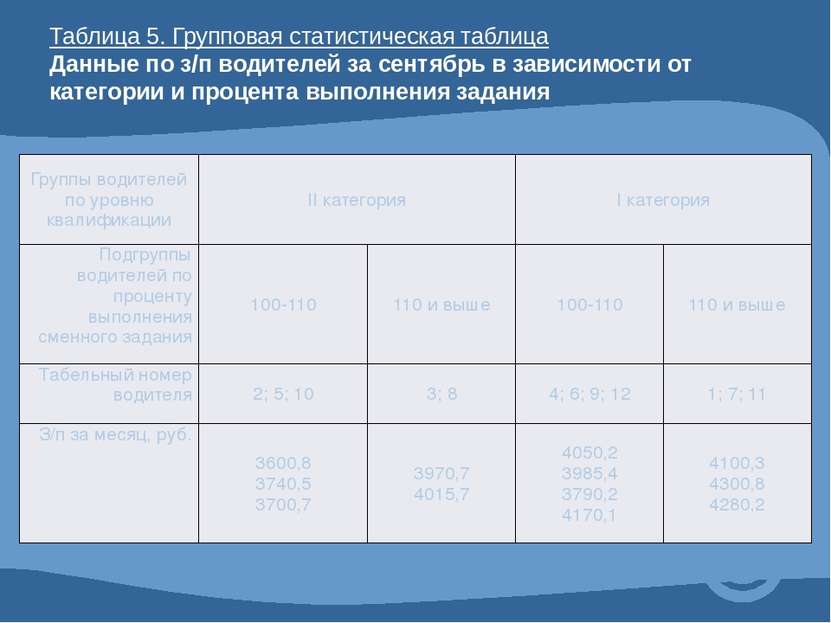
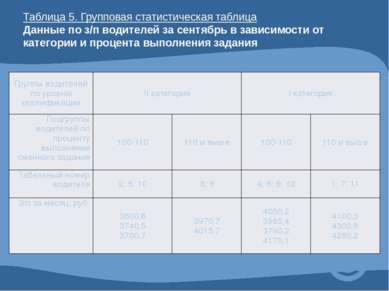Таблица 5. Групповая статистическая таблица Данные по з/п водителей за сентябрь в зависимости от категории и процента выполнения задания Группы водителей по уровню квалификации IIкатегория Iкатегория Подгруппы водителей по проценту выполнения сменного задания 100-110 110 и выше 100-110 110 и выше Табельный номер водителя 2; 5; 10 3; 8 4; 6; 9; 12 1; 7; 11 З/п за месяц, руб. 3600,8 3740,5 3700,7 3970,7 4015,7 4050,2 3985,4 3790,2 4170,1 4100,3 4300,8 4280,2
Cлайд 15
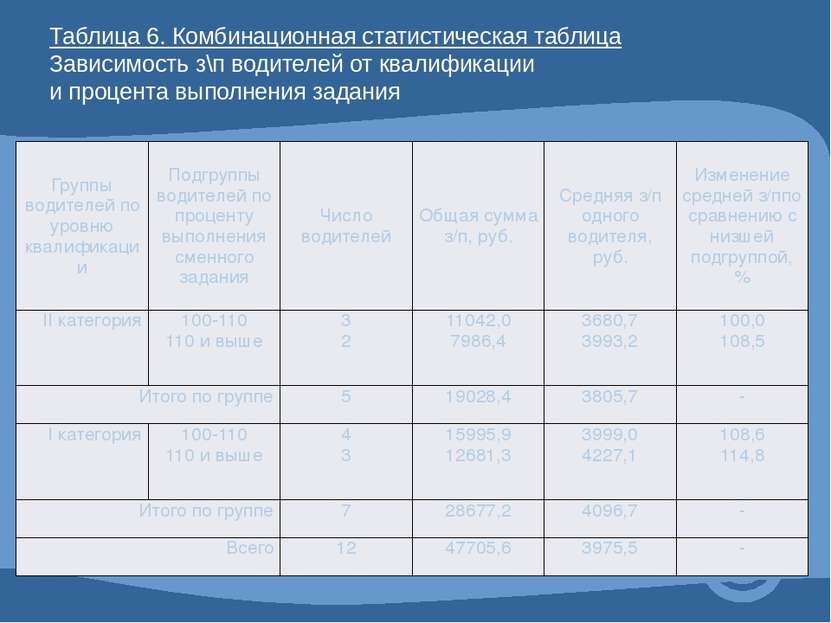
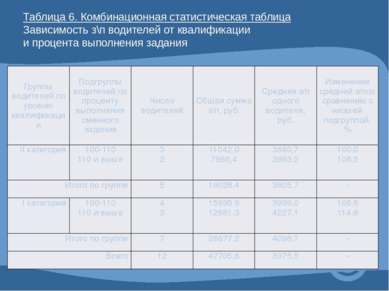Таблица 6. Комбинационная статистическая таблица Зависимость з\п водителей от квалификации и процента выполнения задания Группы водителей по уровню квалификации Подгруппы водителей по проценту выполнения сменного задания Число водителей Общая суммаз/п, руб. Средняя з/п одного водителя, руб. Изменение средней з/ппо сравнению с низшей подгруппой, % IIкатегория 100-110 110 и выше 3 2 11042,0 7986,4 3680,7 3993,2 100,0 108,5 Итого по группе 5 19028,4 3805,7 - Iкатегория 100-110 110 и выше 4 3 15995,9 12681,3 3999,0 4227,1 108,6 114,8 Итого по группе 7 28677,2 4096,7 - Всего 12 47705,6 3975,5 -
Cлайд 16
При составлении таблиц необходимо соблюдать общие правила: таблица должна быть легко обозримой; общий заголовок должен кратко выражать основное содержание; наличие строк «общих итогов»; наличие нумерации строк, которые заполняются данными; соблюдение правила округления чисел.
Cлайд 17
3.3 Ряды распределения
Cлайд 18
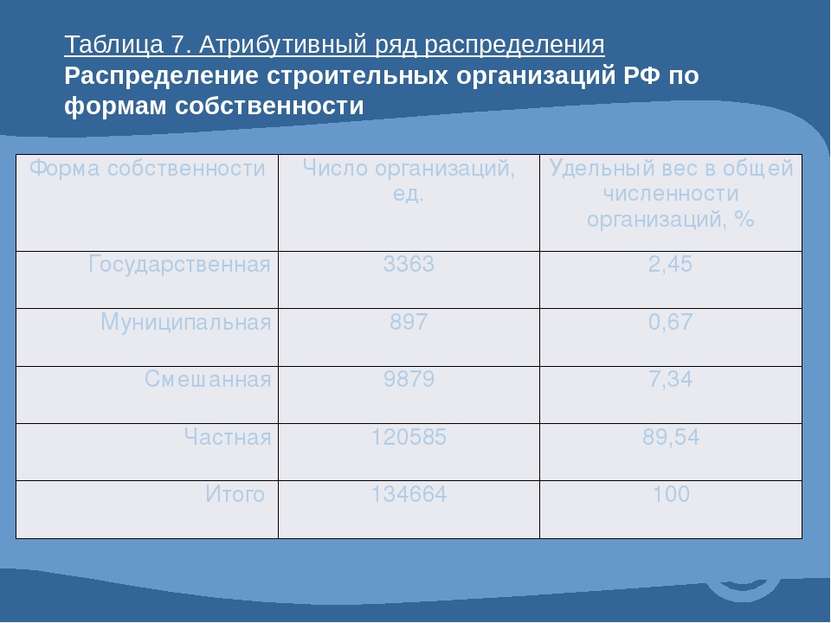
Таблица 7. Атрибутивный ряд распределения Распределение строительных организаций РФ по формам собственности Форма собственности Число организаций, ед. Удельный вес в общей численности организаций, % Государственная 3363 2,45 Муниципальная 897 0,67 Смешанная 9879 7,34 Частная 120585 89,54 Итого 134664 100
Cлайд 19
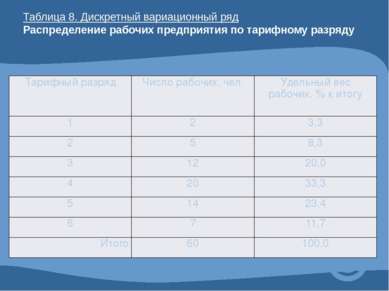Таблица 8. Дискретный вариационный ряд Распределение рабочих предприятия по тарифному разряду Тарифный разряд Число рабочих, чел. Удельный вес рабочих, % к итогу 1 2 3,3 2 5 8,3 3 12 20,0 4 20 33,3 5 14 23,4 6 7 11,7 Итого 60 100,0
Cлайд 20
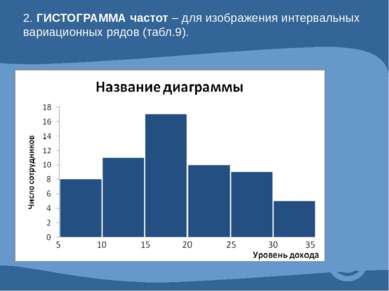
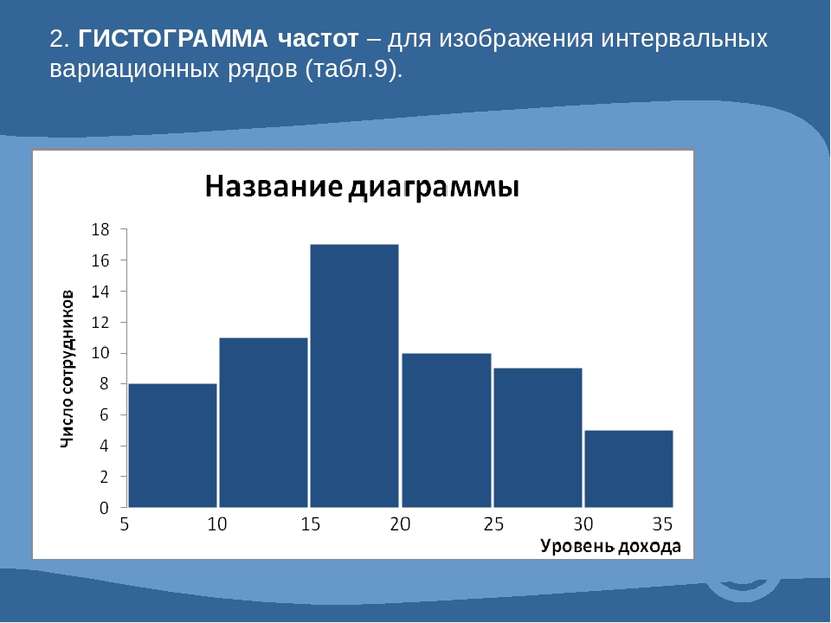
Таблица 9. Интервальный вариационный ряд Распределение сотрудников по уровню доходов Группы сотрудников по уровню дохода, тыс.руб. Число сотрудников Удельный вес сотрудников, % к итогу до 10 8 13,3 10-15 11 18,3 15-20 17 28,3 20-25 10 16,7 25-30 9 15,0 30 и более 5 8,4 Итого 60 100,0
Cлайд 21
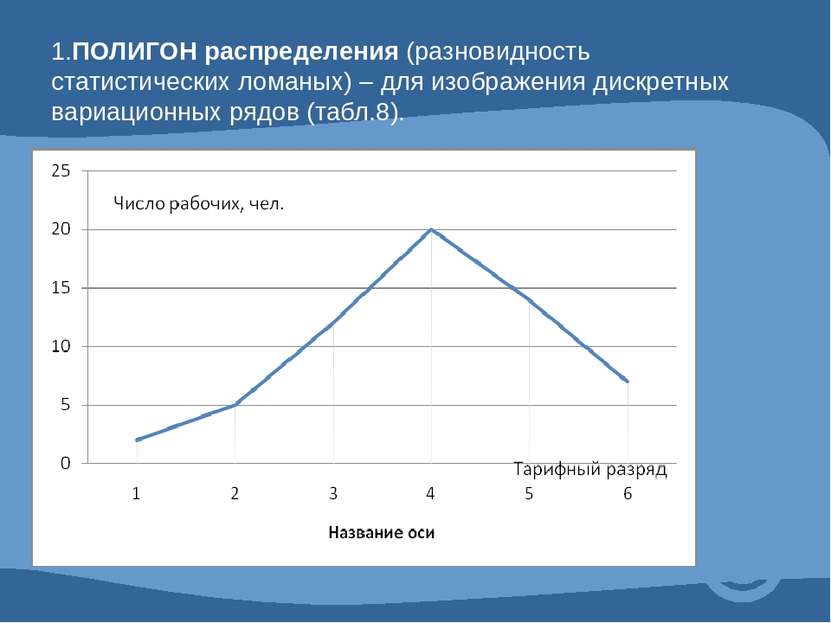
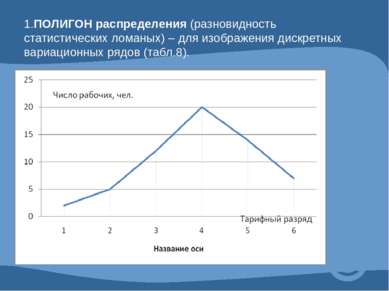1.ПОЛИГОН распределения (разновидность статистических ломаных) – для изображения дискретных вариационных рядов (табл.8).
Cлайд 22
2. ГИСТОГРАММА частот – для изображения интервальных вариационных рядов (табл.9).
Cлайд 23
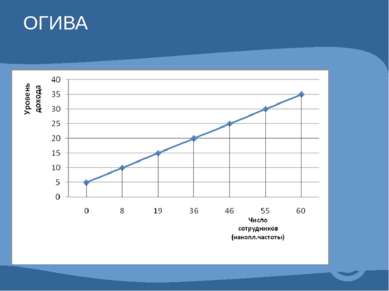
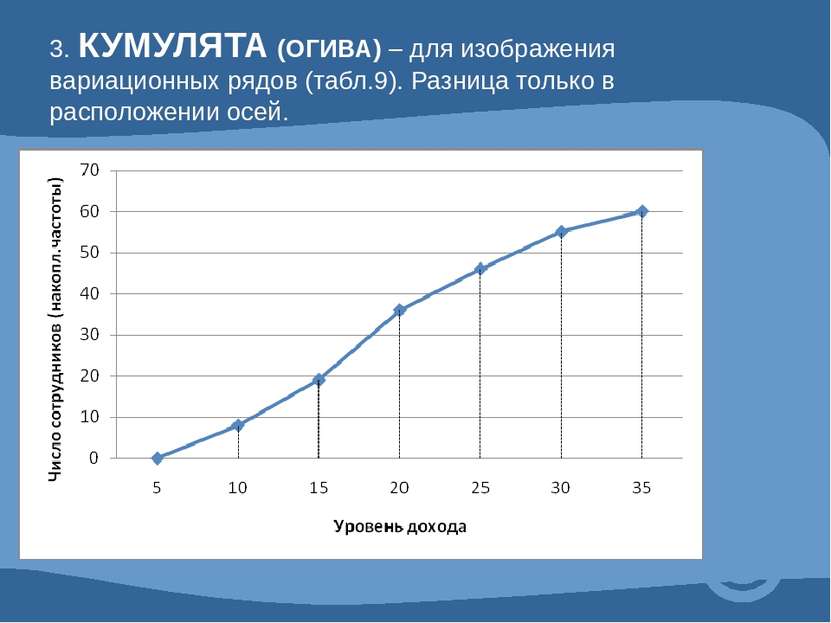
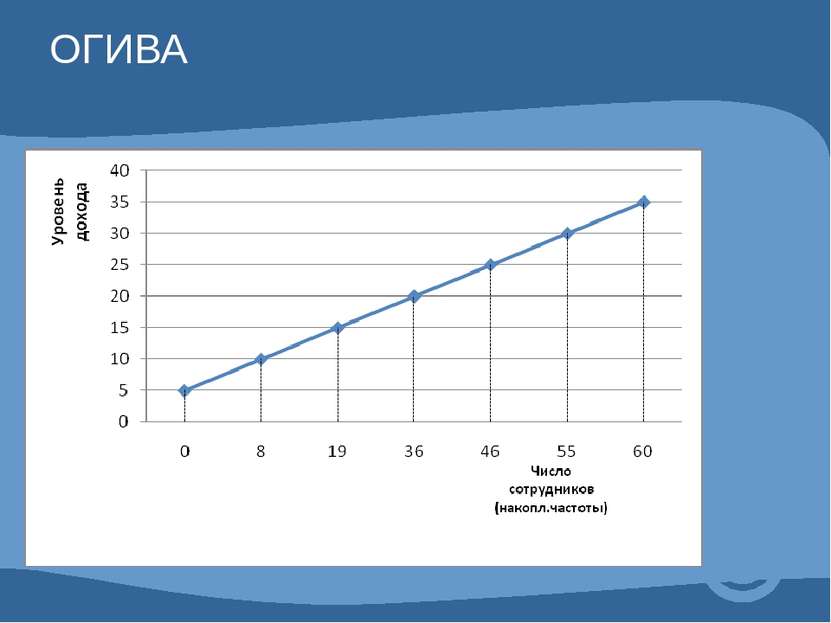
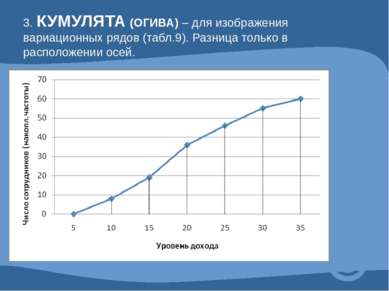3. КУМУЛЯТА (ОГИВА) – для изображения вариационных рядов (табл.9). Разница только в расположении осей.
Cлайд 24
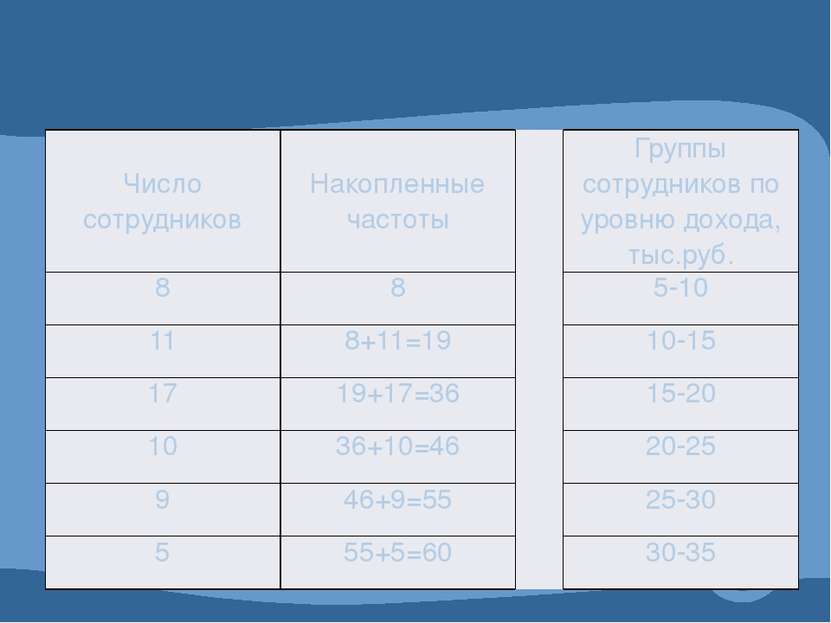
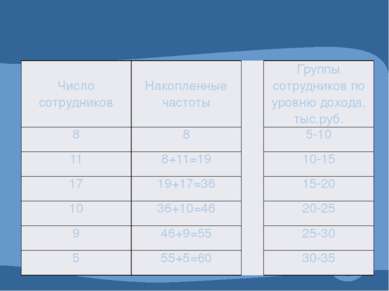Число сотрудников Накопленные частоты Группы сотрудников по уровню дохода, тыс.руб. 8 8 5-10 11 8+11=19 10-15 17 19+17=36 15-20 10 36+10=46 20-25 9 46+9=55 25-30 5 55+5=60 30-35
Cлайд 25
ОГИВА
Cлайд 26
3.4 Кластерный анализ cluster – означает скопление, группу элементов, обладающих общими свойствами. Кластерный анализ — это совокупность методов, позволяющих классифицировать многомерные наблюдения, каждое из которых описывается набором исходных переменных Х1, Х2, ..., Хm. Целью кластерного анализа является образование групп схожих между собой объектов. В отличие от комбинационных группировок кластерный анализ приводит к разбиению на группы с учетом всех групировочных признаков одновременно.
Cлайд 27
Кластеризация – это процесс разбиения множества объектов на кластеры. Слева изображены объекты до кластеризации, а справа – после. Каждый кластер имеет свой цвет.
Cлайд 28
Критерий кластеризации в той или иной мере отражает следующие неформальные требования: • внутри групп объекты должны быть похожи близки друг к другу; • объекты разных групп должны быть далеки друг от друга; • при прочих равных условиях распределения объектов по группам должны быть равномерными.
Cлайд 29
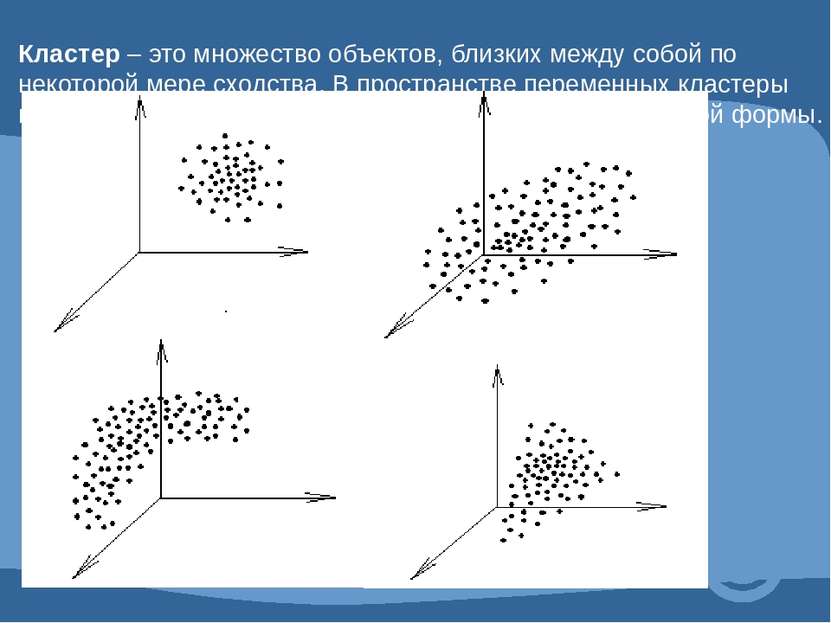
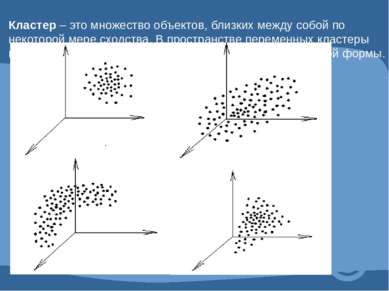Кластер – это множество объектов, близких между собой по некоторой мере сходства. В пространстве переменных кластеры представляют собой скопления точек (объектов) различной формы. 1.Шарообразная форма 2.Эллипсоидная форма 3.Бананообразная форма 4.Конусообразная форма
Cлайд 30
Cлайд 31
Cлайд 32
Наиболее доступно для восприятия и понимания в случае количественных признаков так называемое «евклидово расстояние» или «евклидова метрика». m dij = (Σ (Xik – Xjk)2)1/2 k=1 dij - расстояние между объектами Xik - численное значение i-ой переменной для k-того объекта Xjk - численное значение j-ой переменной для k-того объекта m – количество переменных, которыми описываются объекты *Если имеется два количественных признака, то искомое расстояние будет равно длине гипотенузы прямоугольного треугольника, которая соединяет между собой две точки в прямоугольной системе координат.
Cлайд 33
правила объединения или связи
Cлайд 34
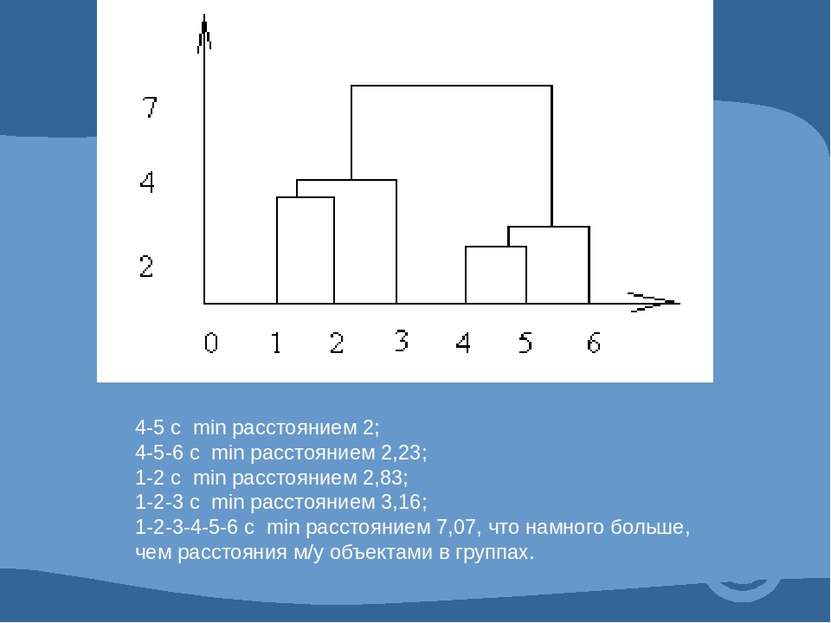
Дендрограмма – графическое изображение результатов процесса последовательной кластеризации, которая осуществляется в терминах матрицы расстояний. С помощью дендрограммы можно графически или геометрически изобразить процедуру кластеризации при условии, что эта процедура оперирует только с элементами матрицы расстояний или сходства. На рисунке показан один из примеров дендрограммы. Он соответствует случаю шести объектов (n=6) и k характеристик (признаков). Объекты А и С наиболее близки и поэтому объединяются в один кластер на уровне близости, равном 0,9. Объекты D и Е объединяются при уровне 0,8. Теперь имеем 4 кластера: (А, С), (F), (D, E), (B). Далее образуются кластеры (А, С, F) и (E, D, B), соответствующие уровню близости, равному 0,7 и 0,6. Окончательно все объекты группируются в один кластер при уровне 0,5.
Cлайд 35
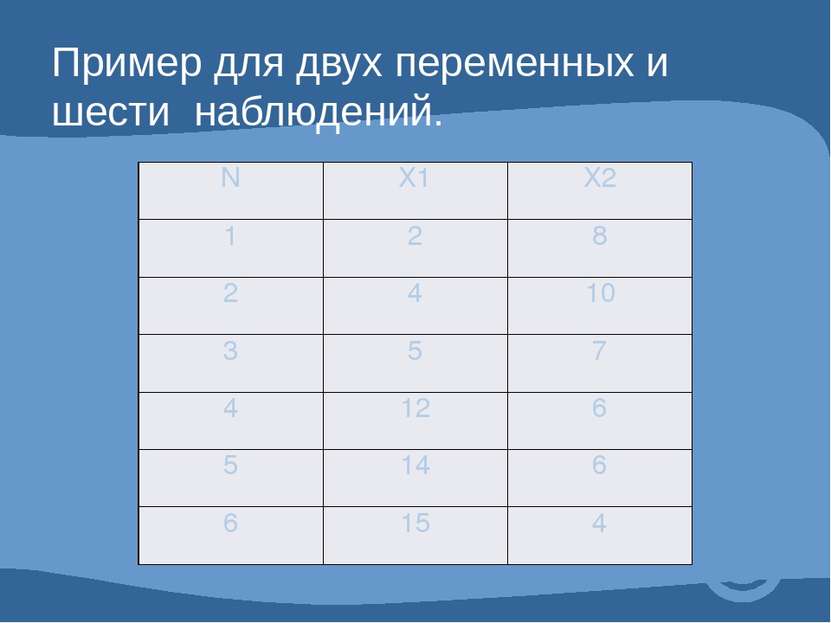
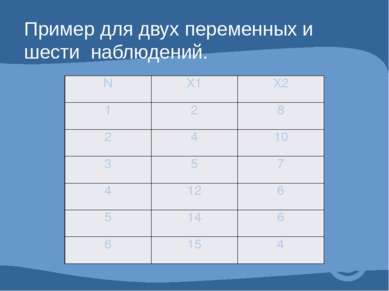Пример для двух переменных и шести наблюдений. N Х1 Х2 1 2 8 2 4 10 3 5 7 4 12 6 5 14 6 6 15 4
Cлайд 36
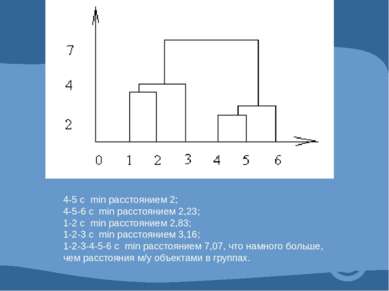
![Рассчитываем расстояния между объектами*: d = [ (2 – 4)2 + (8 – 10)2 ]1/2 = 8...](https://bigslide.ru/images/51/50560/960/img35.jpg "Рассчитываем расстояния между объектами*: d = [ (2 – 4)2 + (8 – 10)2 ]1/2 = 8...")
Рассчитываем расстояния между объектами*: d = [ (2 – 4)2 + (8 – 10)2 ]1/2 = 81/2 = 2,83 d = [ (2 – 5)2 + (8 – 7)2 ]1/2 = 101/2 = 3,16 d = [ (2 – 12)2 + (8 – 6)2 ]1/2 = 1041/2 = 10,2 d = [ (2 – 14)2 + (8 – 6)2 ]1/2 = 1481/2 = 12,16 d = [ (2 – 15)2 + (8 – 4)2 ]1/2 = 1851/2 = 13,6 d = [ (4 – 5)2 + (10 – 7)2 ]1/2 = 101/2 = 3,16 d = [ (4 – 12)2 + (10 – 6)2 ]1/2 = 801/2 = 8,94 d = [ (4 – 14)2 + (10 – 6)2 ]1/2 = 1161/2 = 10,77 d = [ (4 – 15)2 + (10 – 4)2 ]1/2 = 1571/2 = 12,53 d = [ (5 – 12)2 + (7 – 6)2 ]1/2 = 501/2 = 7,07 d = [ (5 – 14)2 + (7 – 6)2 ]1/2 = 821/2 = 9,05 d = [ (5 – 15)2 + (7 – 4)2 ]1/2 = 1091/2 = 10,44 d = [ (12 – 14)2 + (6 – 6)2 ]1/2 = 41/2 = 2 d = [ (12 – 15)2 + (6 – 4)2 ]1/2 = 131/2 = 3,6 d = [ (14 – 15)2 + (6 – 4)2 ]1/2 = 51/2 = 2,23
Cлайд 37
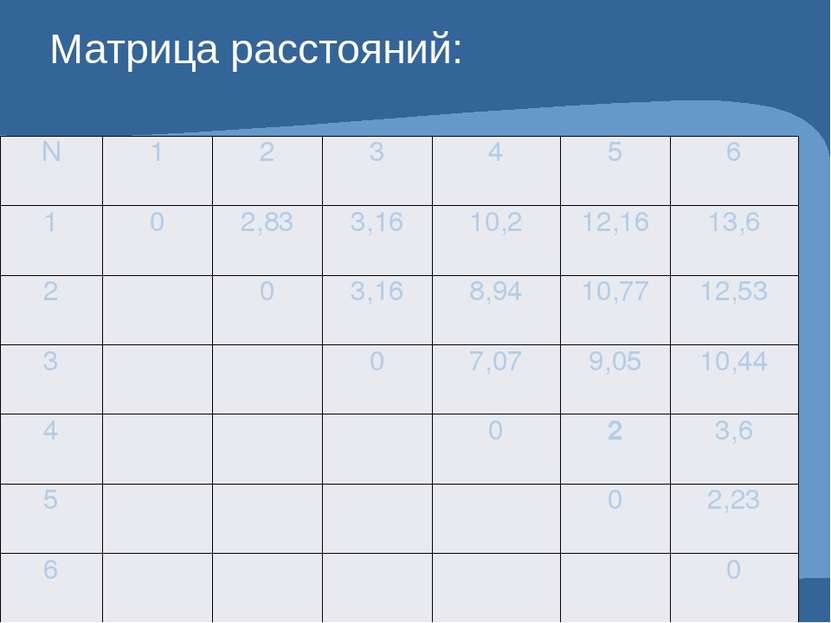
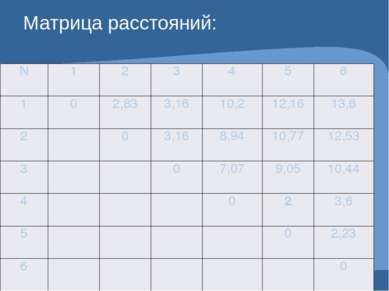Матрица расстояний: N 1 2 3 4 5 6 1 0 2,83 3,16 10,2 12,16 13,6 2 0 3,16 8,94 10,77 12,53 3 0 7,07 9,05 10,44 4 0 2 3,6 5 0 2,23 6 0
Cлайд 38
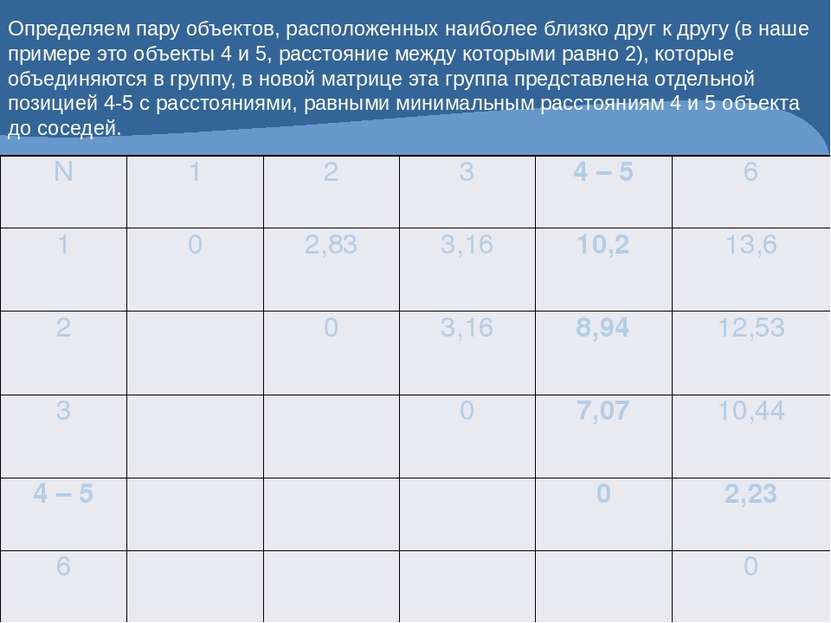
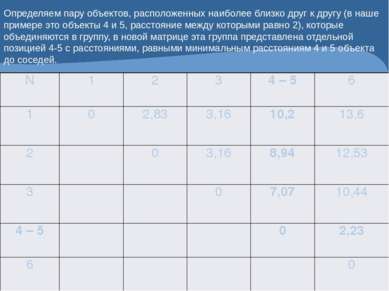Определяем пару объектов, расположенных наиболее близко друг к другу (в наше примере это объекты 4 и 5, расстояние между которыми равно 2), которые объединяются в группу, в новой матрице эта группа представлена отдельной позицией 4-5 с расстояниями, равными минимальным расстояниям 4 и 5 объекта до соседей. N 1 2 3 4 – 5 6 1 0 2,83 3,16 10,2 13,6 2 0 3,16 8,94 12,53 3 0 7,07 10,44 4 – 5 0 2,23 6 0
Cлайд 39
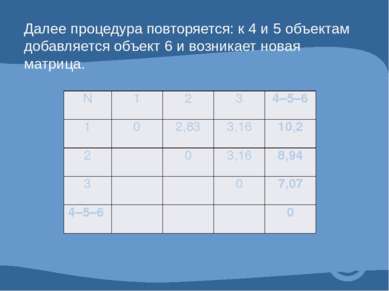Далее процедура повторяется: к 4 и 5 объектам добавляется объект 6 и возникает новая матрица. N 1 2 3 4–5–6 1 0 2,83 3,16 10,2 2 0 3,16 8,94 3 0 7,07 4–5–6 0
Cлайд 40
Далее, ближайшее расстояние между 1 и 2 объектами, появляется новая группа 1-2. N 1-2 3 4-5-6 1-2 0 3,16 8,94 3 0 7,07 4-5-6 0
Cлайд 41
Далее объект 3 присоединяется к группе 1-2, как к ближайшей. Выявились два кластера в данной совокупности объектов, между которыми ближайшее расстояние 7,07, что намного больше, чем расстояния между объектами в группах. N 1-2-3 4-5-6 1-2-3 0 7,07 4-5-6 0
Cлайд 42
4-5 с min расстоянием 2; 4-5-6 с min расстоянием 2,23; 1-2 с min расстоянием 2,83; 1-2-3 с min расстоянием 3,16; 1-2-3-4-5-6 с min расстоянием 7,07, что намного больше, чем расстояния м/у объектами в группах.
