X
Код презентации скопируйте его
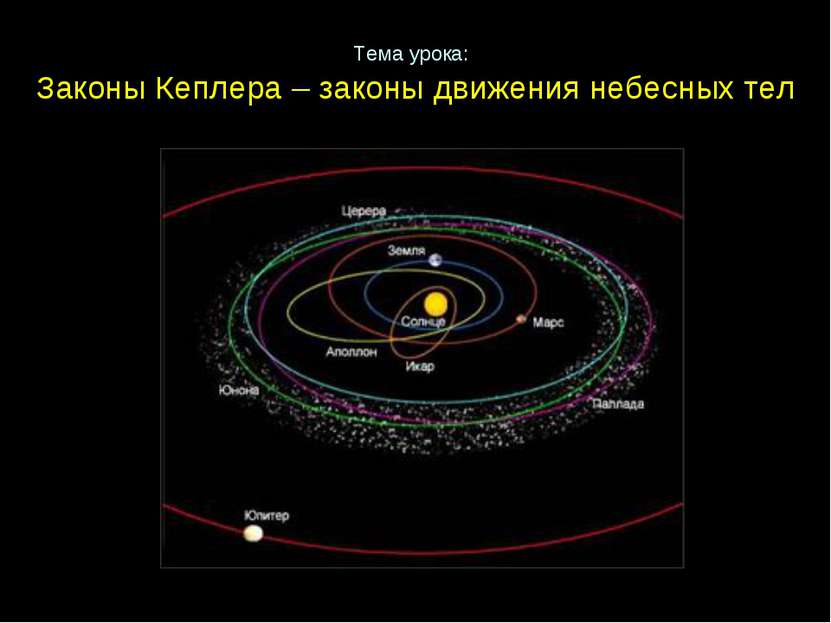
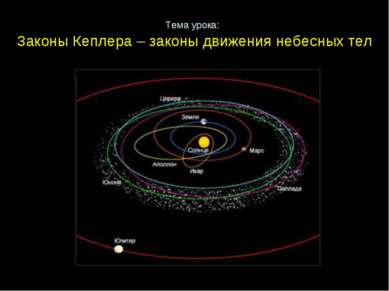
Законы Кеплера
Скачать эту презентацию
Презентация на тему Законы Кеплера
Скачать эту презентациюCлайд 1
Тема урока: Законы Кеплера – законы движения небесных тел
Cлайд 2
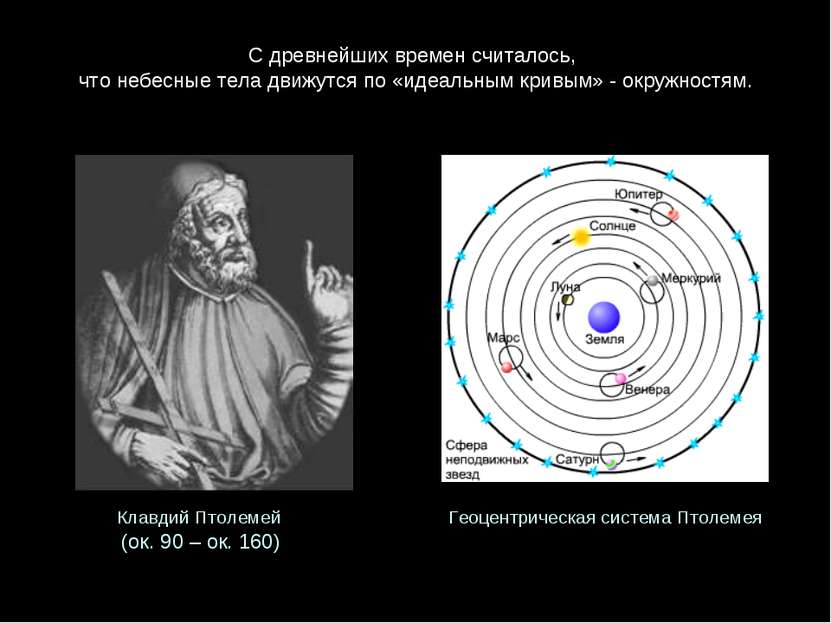
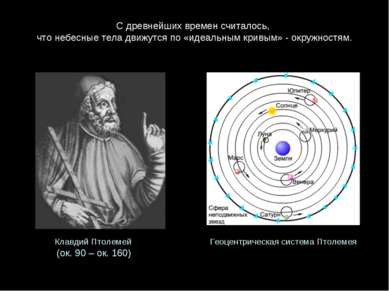С древнейших времен считалось, что небесные тела движутся по «идеальным кривым» - окружностям. Геоцентрическая система Птолемея Клавдий Птолемей (ок. 90 – ок. 160)
Cлайд 3
В теории Николая Коперника, создателя гелиоцентрической системы мира, круговое движение также не подвергалось сомнению. Николай Коперник (1473–1543) Гелиоцентрическая система мира Коперника
Cлайд 4
Наблюдаемое положение планет не соответствовало предвычисленному в соответствии с теорией кругового движения планет вокруг Солнца. Почему? В XVII веке ответ на этот вопрос искал немецкий астроном Иоганн Кеплер. Иоганн Кеплер (1571–1630 )
Cлайд 5
Тихо Браге (1546-1601) Иоганн Кеплер изучал движение Марса по результатам многолетних наблюдений датского астронома Тихо Браге.
Cлайд 6
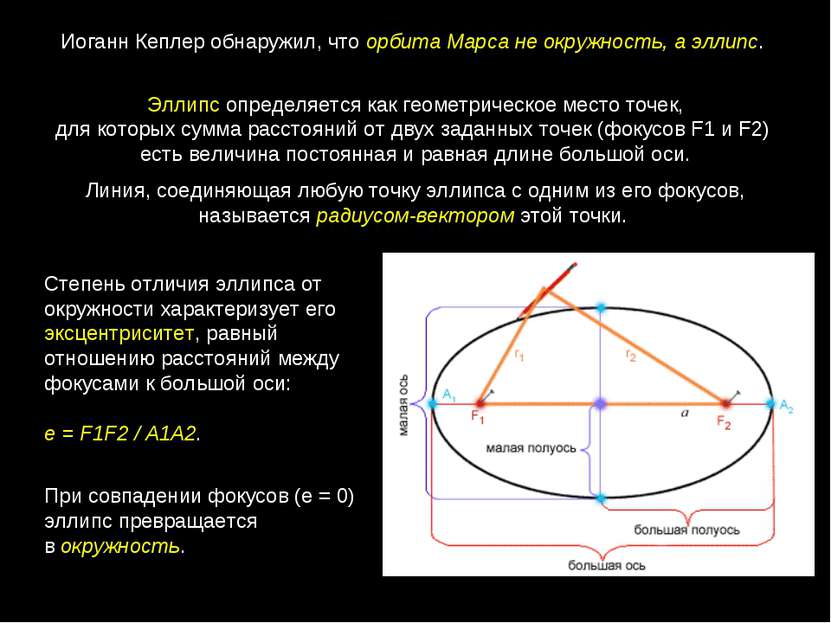
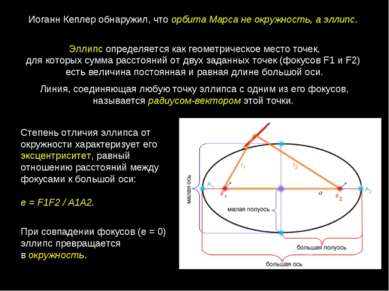Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов F1 и F2) есть величина постоянная и равная длине большой оси. Линия, соединяющая любую точку эллипса с одним из его фокусов, называется радиусом-вектором этой точки. Иоганн Кеплер обнаружил, что орбита Марса не окружность, а эллипс. Степень отличия эллипса от окружности характеризует его эксцентриситет, равный отношению расстояний между фокусами к большой оси: е = F1F2 / A1A2. При совпадении фокусов (е = 0) эллипс превращается в окружность.
Cлайд 7
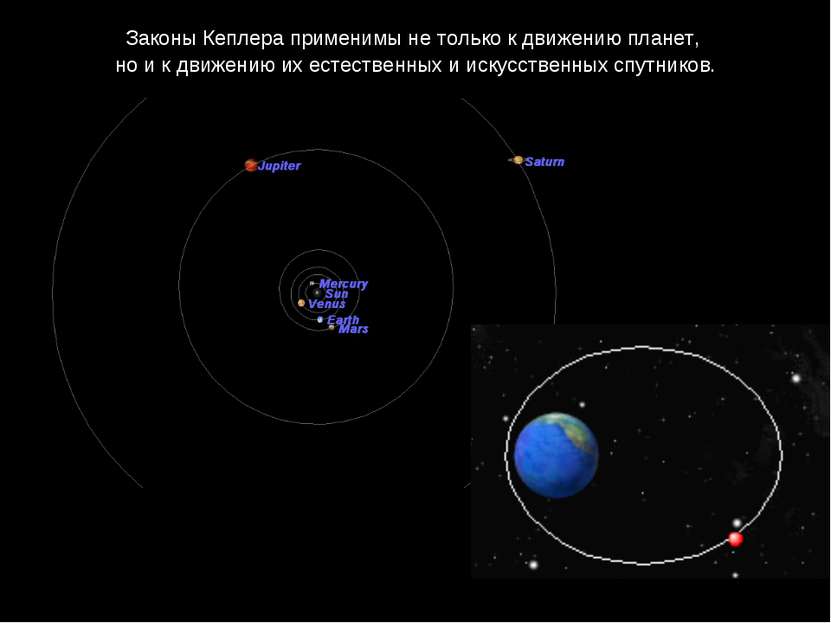
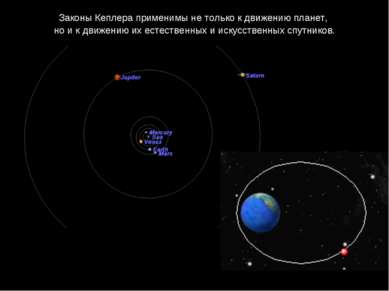Законы Кеплера применимы не только к движению планет, но и к движению их естественных и искусственных спутников.
Cлайд 8
Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Первый закон Кеплера: Иллюстрация первого закона Кеплера на примере движения спутников Земли
Cлайд 9
Орбиты планет – эллипсы, мало отличающиеся от окружностей, так как их эксцентриситеты малы.
Cлайд 10
Большая полуось орбиты планеты – это ее среднее расстояние от Солнца. Среднее расстояние Земли от Солнца принято в астрономии за единицу расстояния и называется астрономической единицей: 1 а.е. = 149 600 000 км. Ближайшую к Солнцу точку орбиты называют перигелием (греч. пери – возле, около; Гелиос – Солнце), а наиболее удаленную – афелием (греч. апо – вдали).
Cлайд 11
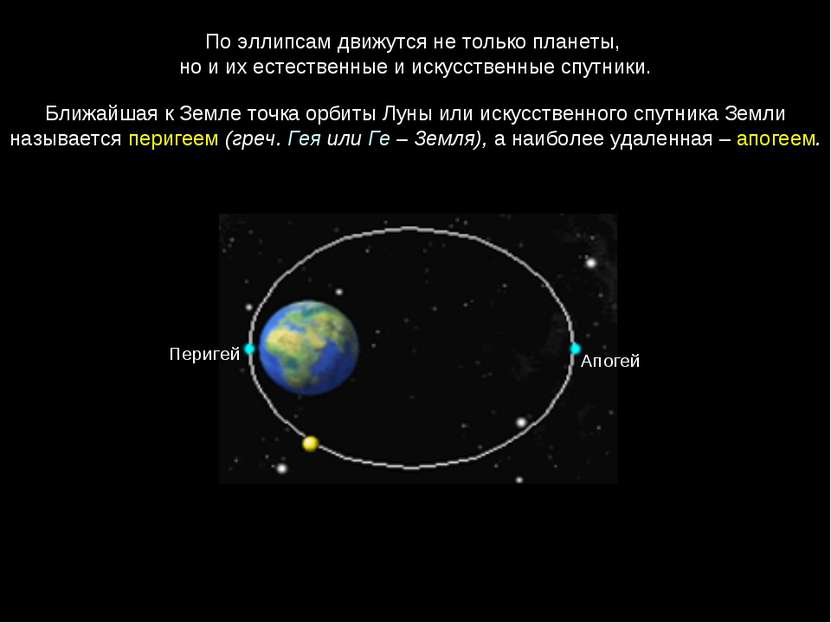
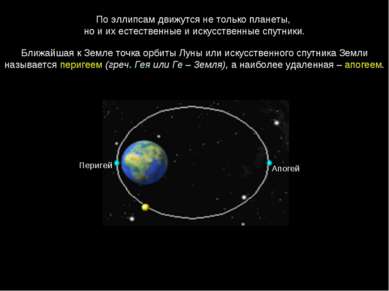По эллипсам движутся не только планеты, но и их естественные и искусственные спутники. Ближайшая к Земле точка орбиты Луны или искусственного спутника Земли называется перигеем (греч. Гея или Ге – Земля), а наиболее удаленная – апогеем. Перигей Апогей
Cлайд 12
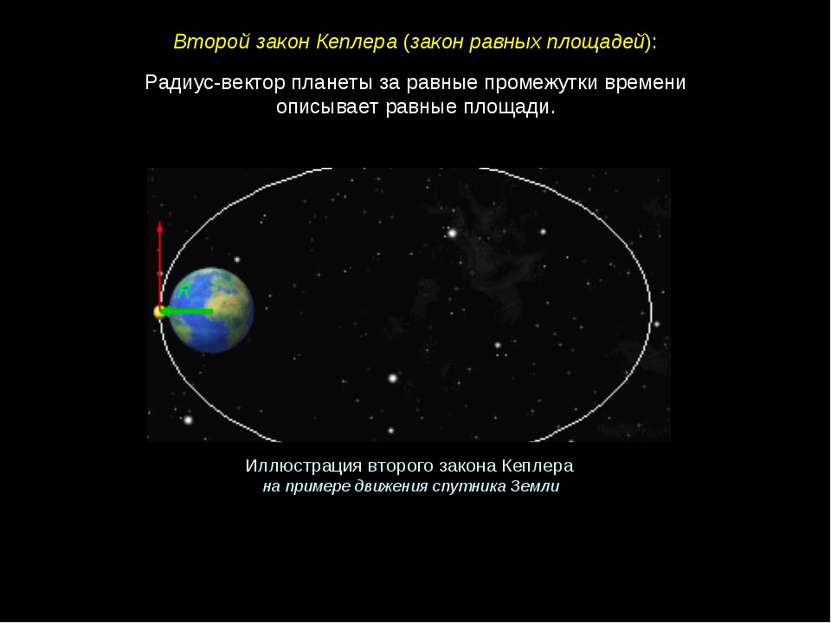
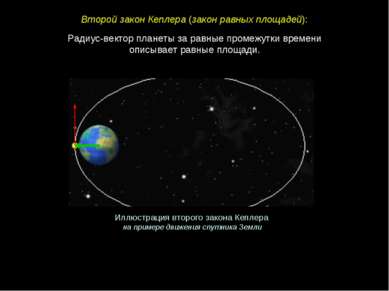Радиус-вектор планеты за равные промежутки времени описывает равные площади. Второй закон Кеплера (закон равных площадей): Иллюстрация второго закона Кеплера на примере движения спутника Земли
Cлайд 13
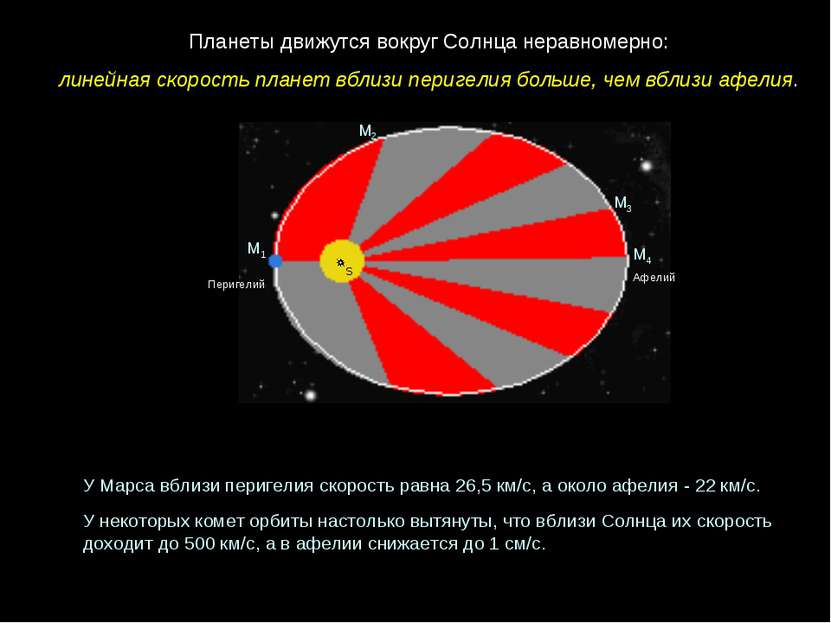
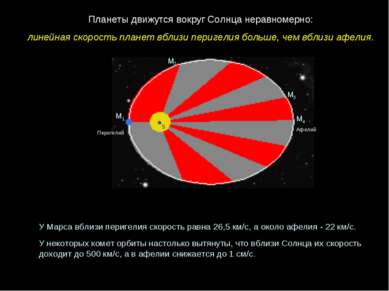Перигелий Афелий М1 М2 М3 М4 Планеты движутся вокруг Солнца неравномерно: линейная скорость планет вблизи перигелия больше, чем вблизи афелия. У Марса вблизи перигелия скорость равна 26,5 км/с, а около афелия - 22 км/с. У некоторых комет орбиты настолько вытянуты, что вблизи Солнца их скорость доходит до 500 км/с, а в афелии снижается до 1 см/с. S
Cлайд 14
Квадраты сидерических периодов обращений двух планет относятся как кубы больших полуосей их орбит: Третий закон Кеплера: Иллюстрация третьего закона Кеплера на примере движения спутников Земли
Cлайд 15
Скорости близких к Солнцу планет значительно больше, чем скорости далеких.
Cлайд 16
Квадраты сидерических периодов обращений двух планет относятся как кубы больших полуосей их орбит. Третий закон Кеплера Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Первый закон Кеплера Второй закон Кеплера Радиус-вектор планеты за равные промежутки времени описывает равные площади. Кеплер исследовал движения всех известных в то время планет и эмпирически вывел три закона движения планет относительно Солнца.
Cлайд 17
Какое расстояние называется астрономической единицей? Среднее расстояние Земли от Солнца называется астрономической единицей. Чему равна одна астрономическая единица? 1 а.е. = 149 600 000 км
Cлайд 18
Квадраты сидерических периодов обращений двух планет относятся как кубы больших полуосей их орбит. Третий закон Кеплера Каждая планета движется по эллипсу, в одном из фокусов которого находится Солнце. Первый закон Кеплера Второй закон Кеплера Радиус-вектор планеты за равные промежутки времени описывает равные площади.
Cлайд 19
Замечено, что противостояния некоторой планеты повторяются через 2 года. Чему равна большая полуось ее орбиты? 1 2 3 4 Задача.
