X
Код презентации скопируйте его
Тайны паркетов
Скачать эту презентацию
Презентация на тему Тайны паркетов
Скачать эту презентациюCлайд 1
МОУ Октябрьская средняя общеобразовательная школа Радищевского района Ульяновской области Выполнил ученик 8 класса Волик Павел Руководитель Волик Т.Г., учитель математики п. Октябрьский 2010
Cлайд 2
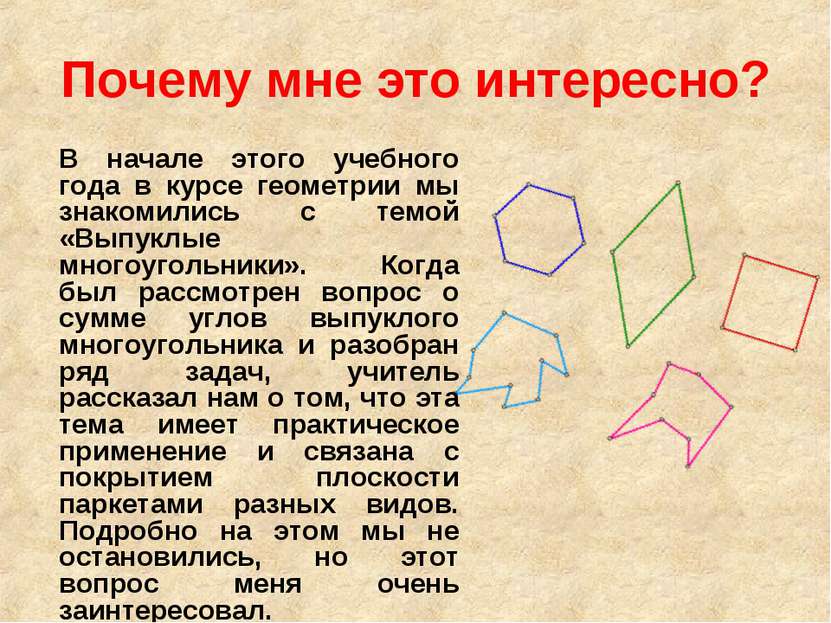
Почему мне это интересно? В начале этого учебного года в курсе геометрии мы знакомились с темой «Выпуклые многоугольники». Когда был рассмотрен вопрос о сумме углов выпуклого многоугольника и разобран ряд задач, учитель рассказал нам о том, что эта тема имеет практическое применение и связана с покрытием плоскости паркетами разных видов. Подробно на этом мы не остановились, но этот вопрос меня очень заинтересовал.
Cлайд 3
Я решил узнать: Что такое паркет? Как проверить собственную гипотезу? Каково прикладное значение выбран-ной мной темы ? Только ли ученые- математики занимаются этой темой? Какие бывают виды паркетов? Какими фигурами можно покрыть плоскость? Какова история паркета?
Cлайд 4
Я выдвинул гипотезу: паркеты можно составлять только из правильных многоугольников и этих паркетов - конечное множество. Цель данного проекта: исследовать вопрос о покрытии плоскости многоугольниками.
Cлайд 5
Для достижения цели я поставил перед собой следующие задачи: 1) найти источники дополнительной информации -о истории возникновения паркетов; -о видах паркетов; -о многоугольниках, с помощью которых можно составить паркет; 2) провести исследование, выясняющее, насколько верна выдвинутая мной гипотеза; 3) проанализировать, обобщить и систематизировать полученные данные; 4) подобрать иллюстрации и оформить презентацию «Тайны паркетов»; 5) ознакомить с результатами проекта учащихся 7-9 классов на уроках геометрии.
Cлайд 6
Что такое паркет? Паркет (франц. parquet)- небольшие древесные, строганные планки для покрытия пола. С XVI в. известен в России. Паркет изготавливают преимущественно из твердых пород дерева, для художественного паркета используют ценные породы. Паркет – это настил на полу из дощечек, уложенный так, что они образуют какой-нибудь рисунок (словарь С.И.Ожегова); Паркет – это такое покрытие плоскости правильными многоугольниками, при котором два многоугольника имеют либо общую сторону, либо общую вершину или совсем не имеют общих точек («Энциклопедический словарь юного математика»); Паркет - бесконечное семейство многоугольников, покрывающее плоскость без просветов и двойных покрытий.
Cлайд 7
Паркеты из правильных многоугольников Паркет называется правильным, если он составлен из равных правильных многоугольников и вокруг каждой вершины правильные многоугольники расположены одним и тем же способом. Если при составлении паркета использовать несколько правильных многоугольников с различным числом сторон, то такой паркет называется полуправильным.
Cлайд 8
В вершине паркета может сходиться не более шести и не менее трех многоугольников. Действительно, при схождении в одной вершине семи или более многоугольников хотя бы один угол в правильном многоугольнике должен быть менее 60°, что невозможно (минимальный угол — у треугольника — равен 60°). При схождении в одной вершине двух многоугольников у одного из них внутренний угол должен быть более 180°, что, очевидно, также невозможно. Таким образом, решение задачи распадается на анализ тех вариантов, когда в вершине паркета сходятся 3, 4, 5 и 6 правильных многоугольников.
Cлайд 9
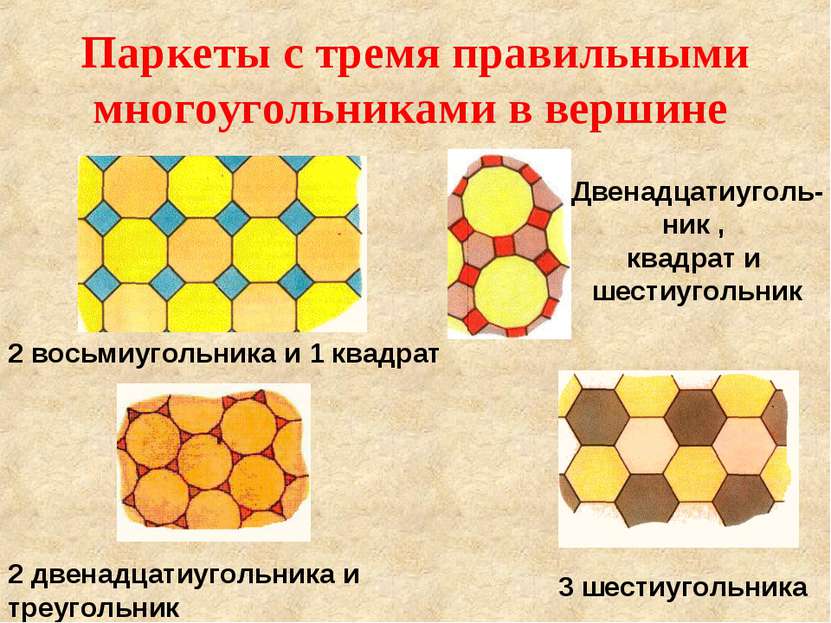
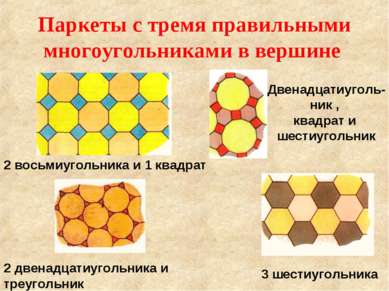Паркеты с тремя правильными многоугольниками в вершине 3 шестиугольника 2 восьмиугольника и 1 квадрат Двенадцатиуголь- ник , квадрат и шестиугольник 2 двенадцатиугольника и треугольник
Cлайд 10
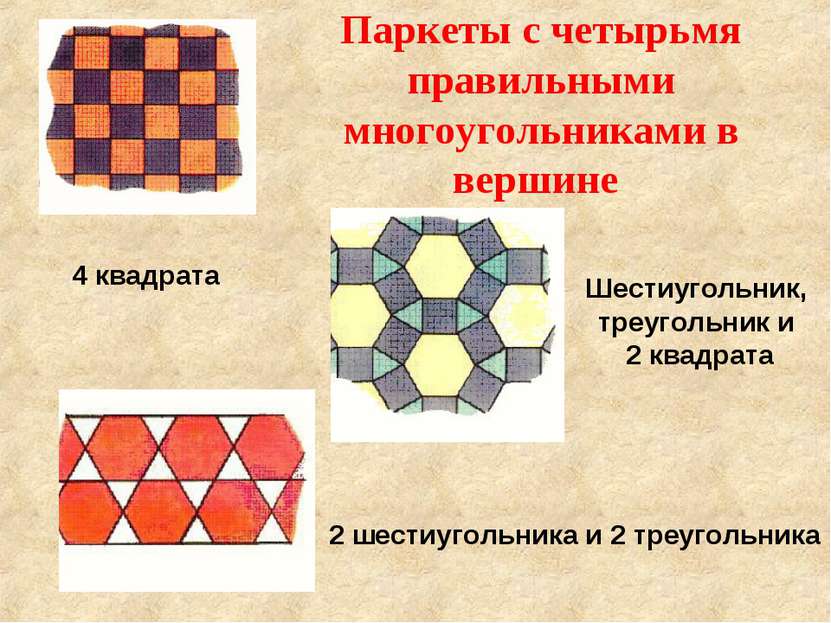
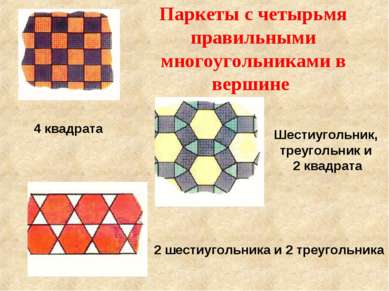Паркеты с четырьмя правильными многоугольниками в вершине 4 квадрата Шестиугольник, треугольник и 2 квадрата 2 шестиугольника и 2 треугольника
Cлайд 11
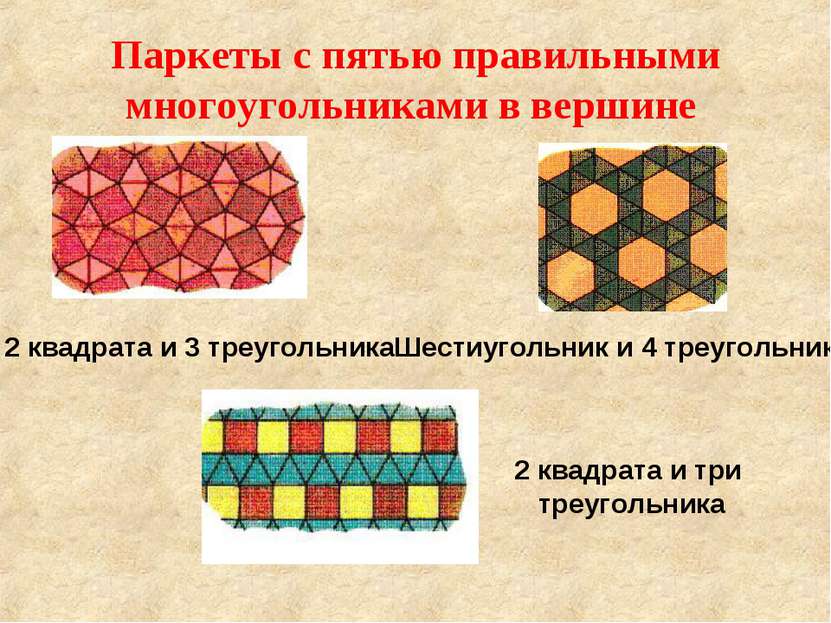
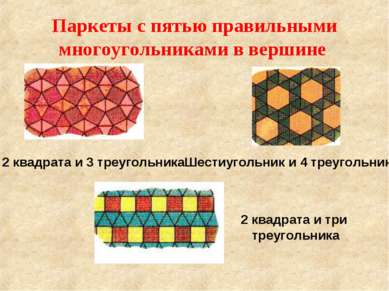Паркеты с пятью правильными многоугольниками в вершине 2 квадрата и 3 треугольника Шестиугольник и 4 треугольника 2 квадрата и три треугольника
Cлайд 12
Паркеты с шестью правильными многоугольниками в вершине 6 треугольников
Cлайд 13
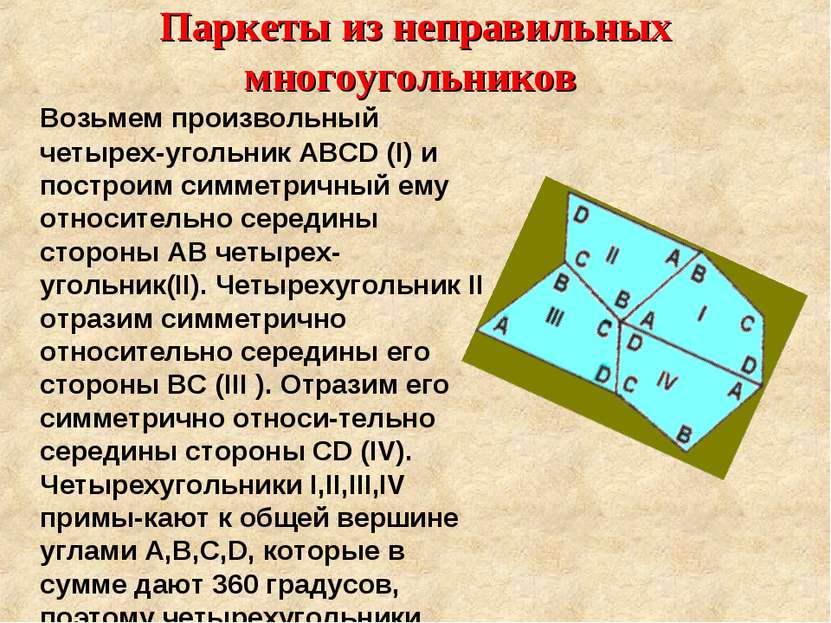
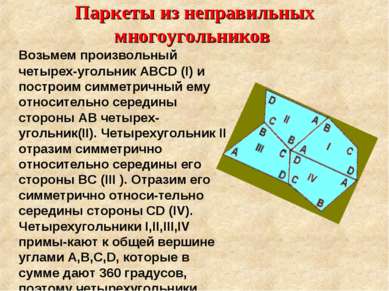Паркеты из неправильных многоугольников Возьмем произвольный четырех-угольник ABCD (I) и построим симметричный ему относительно середины стороны АВ четырех-угольник(II). Четырехугольник II отразим симметрично относительно середины его стороны ВС (III ). Отразим его симметрично относи-тельно середины стороны CD (IV). Четырехугольники I,II,III,IV примы-кают к общей вершине углами A,B,C,D, которые в сумме дают 360 градусов, поэтому четырехугольники заполнят плоскость вокруг общей вершины.
Cлайд 14
Паркеты из неправильных многоугольников Вообще можно покрыть плоскость копиями произвольного многоугольника, необязательно выпуклого:
Cлайд 15
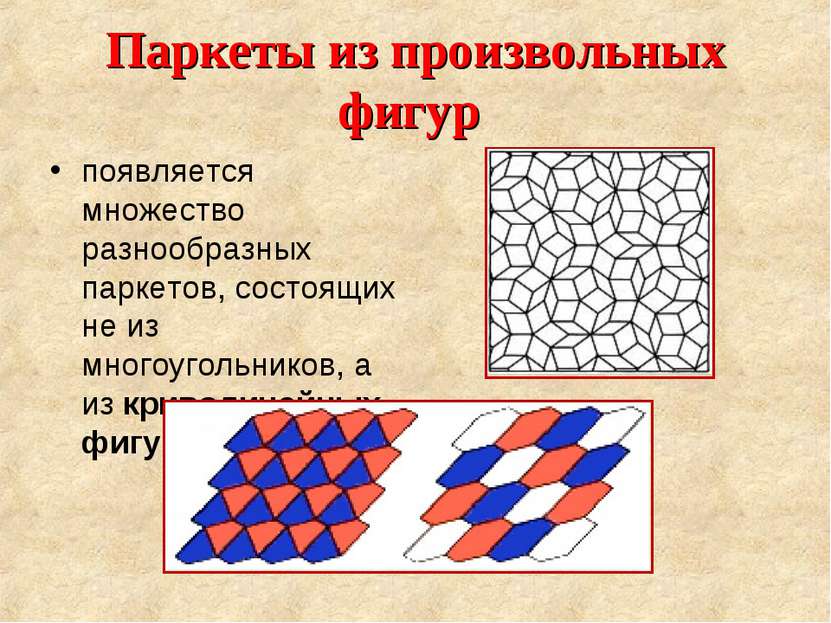
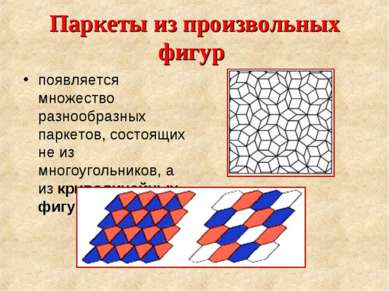Паркеты из произвольных фигур появляется множество разнообразных паркетов, состоящих не из многоугольников, а из криволинейных фигур
Cлайд 16
Паркеты из произвольных фигур Всемирная известность пришла к Эшеру в 1951 году. В 1954 году в Амстердаме состоялась большая выставка Эшера, приуроченная к Международному математическому конгрессу. Математики сразу признали художника «своим»; с этого времени его рисунки – неизменный атрибут физико-математических изданий. Знаменитый голландский художник Мариус Эшер (1898-1972).
Cлайд 17
Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости. Регулярное разбиение плоскости, называемое «мозаикой», - это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Эшер интересовался всеми видами мозаик, а также ввел собственный вид, который назвал «метаморфозами», где фигуры изменяются и взаимодействуют друг с другом.
Cлайд 18
Мариус Эшер посвятил орнаментам несколько своих картин. Среди них: «Всадники», «Летящие птицы»; «Ящерицы».
Cлайд 19
Способы построения паркетов Способ первый. Берем некоторую уже известный нам паркет и выполняем преобразования: сжатие или растяжение, замена прямолинейных отрезков кривыми с началом и концом в тех же точках, что и у отрезков... Пример: паркеты, полученные заменой отрезков "квадратной" сетки некоторыми кривыми или ломаными.
Cлайд 20
Способы построения паркетов Способ второй. Объединяем отдельные элементы уже существующих паркетов. Примеры: паркеты, полученные в результате объединения элементов квадратной сетки.
Cлайд 21
Способы построения паркетов Способ третий. Берем существующую сетку и дополняем ее новыми линиями. Получаем разбиение плоскости на фигуры, которые затем можно по-новому объединить.
Cлайд 22
Способы построения паркетов Способ четвертый. Выбираем некоторую кривую или ломаную и начинаем ее переносить, поворачивать, отражать... получившиеся кривые или ломаные размещаем на плоскости таким образом, чтобы они образовали замкнутые контуры (которые в дальнейшем будут рассматриваться как элементы паркета).
Cлайд 23
Подводя итоги... Мне удалось: - выяснить, что такое паркет с точки зрения математики; - узнать много нового и интересного об истории возникновения паркетов; - найти в литературе и в Интернете сведения о том, какие виды паркетов существуют; провести собственное исследование вопроса о построении паркетов и убедиться в том, что паркетов из правильных многоугольников – конечное число, а именно 11, а также опровергнуть гипотезу о том, что паркеты можно составить только из правильных многоугольников; подобрать иллюстрации и оформить с помощью руководителя и презентацию «Тайны паркетов»; - ознакомить с результатами проекта учащихся 7-9 классов.
Cлайд 24
Спасибо за внимание!!! Мой адрес: Ульяновская обл., Радищевский р-н, п. Октябрьский, ул. Мира, д. 30, кв. 7.
