X
Код презентации скопируйте его
Преобразования графиков функций
Скачать эту презентацию
Презентация на тему Преобразования графиков функций
Скачать эту презентациюCлайд 1
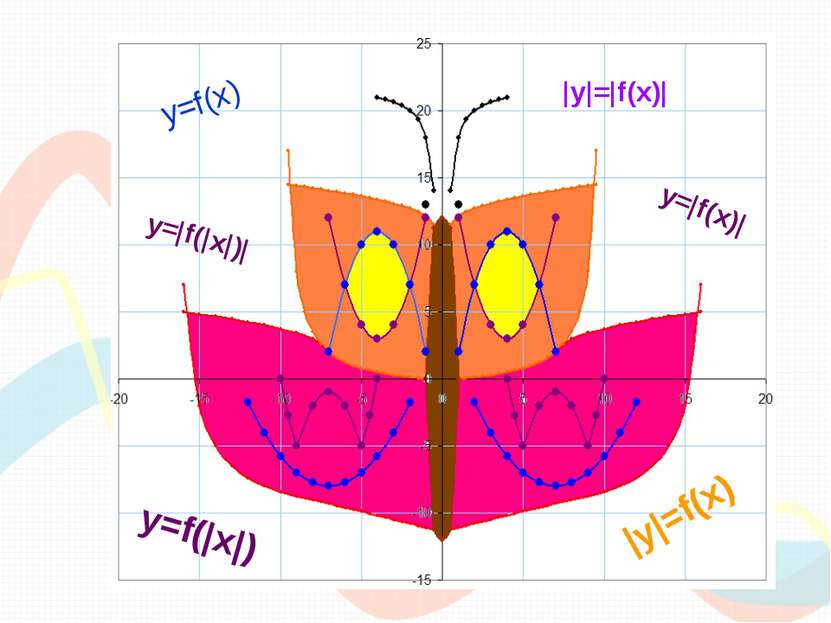
Преобразования графиков функций Исследовательская работа Выполнена ученицей 10 а класса МОУ СОШ №1 г.Архангельска Тёмкиной Валентиной Сергеевной Научные руководители: учитель математики ВКК МОУ СОШ №1 г.Архангельска Котцова Ольга Валентиновна учитель информатики и ИКТ ГБОУ АО Кадетская школа-интернат «Архангельский морской кадетский корпус» 2012
Cлайд 2
y=f(x) y=|f(x)| y=f(|x|) |y|=f(x) |y|=|f(x)| y=|f(|x|)|
Cлайд 3
Актуальность: Эта тема актуальна, т.к. в конце 11 класса необходимо сдавать единый государственный экзамен по математике, куда будут включены задания, связанные с преобразованием графиков функций. Нами были проанализированы различные собрания с экзаменационными заданиями. Вывод: в сборниках КИМ единого государственного экзамена по математике встречаются задания на использование знаний о различных преобразованиях графиков функций.
Cлайд 4
Цель: Изучение способов построения графиков функций с помощью различных преобразований. Задачи: Исследовать взаимосвязь графика функции y=f(x) с графиками функций y=|f(x)|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a). Рассмотреть задания на построение графиков функций с помощью преобразований. Попробовать создать рисунок, используя исследуемые функции. Узнать, есть ли более профессиональные и эффективные системы для построения графиков в декартовых системах координат кроме Excel и Calc, которые мы использовали для построения в прошлой работе. Выявить в чём преимущества и недостатки этих компьютерных программ.
Cлайд 5
Рабочая гипотеза: графики сложных функций, можно построить с помощью преобразований графика исходной функции. Объект – графики функций. Предмет – построение графиков сложных функций с помощью преобразования графика исходной функции. Методы исследования: наблюдения, сравнения, анализ, обобщение, прогнозирование, знаковое моделирование.
Cлайд 6
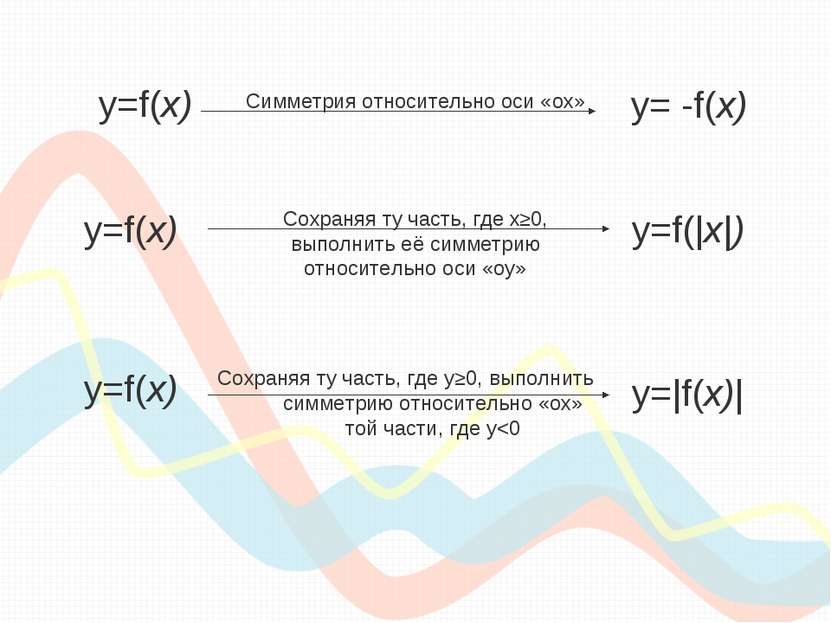
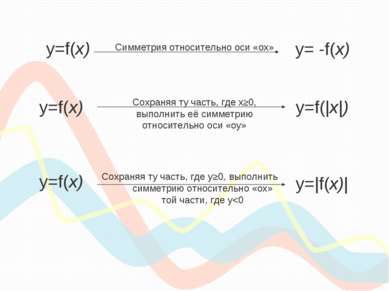y=f(х) y= -f(х) Симметрия относительно оси «ох» y=f(х) y=f(|х|) Сохраняя ту часть, где х≥0, выполнить её симметрию относительно оси «оу» y=|f(х)| y=f(х) Сохраняя ту часть, где у≥0, выполнить симметрию относительно «ох» той части, где у
Cлайд 7
y=cos х y=cos |x| y=cos х y= -cos x y=cos х y=|cos x| ? ? ?
Cлайд 8
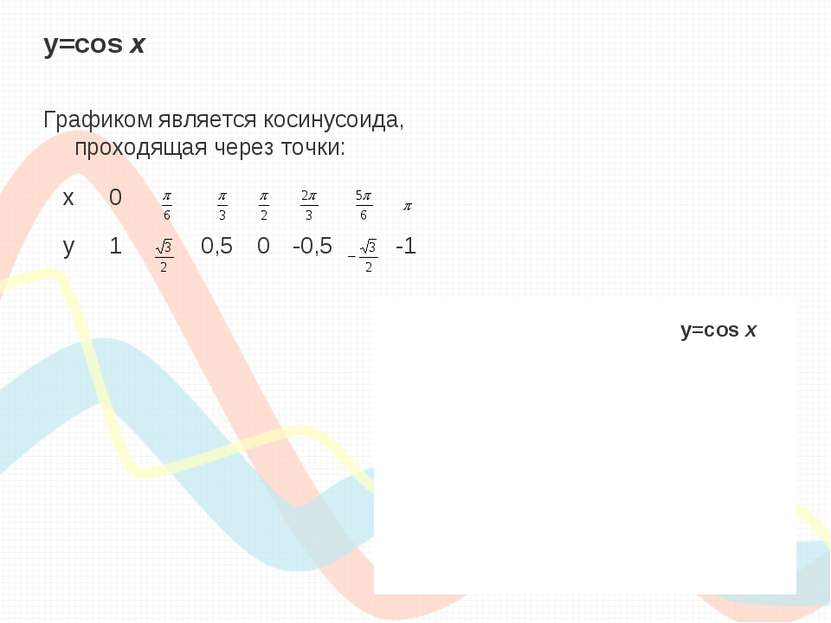
y=cos х Графиком является косинусоида, проходящая через точки: y=cos х x 0 y 1 0,5 0 -0,5 -1
Cлайд 9
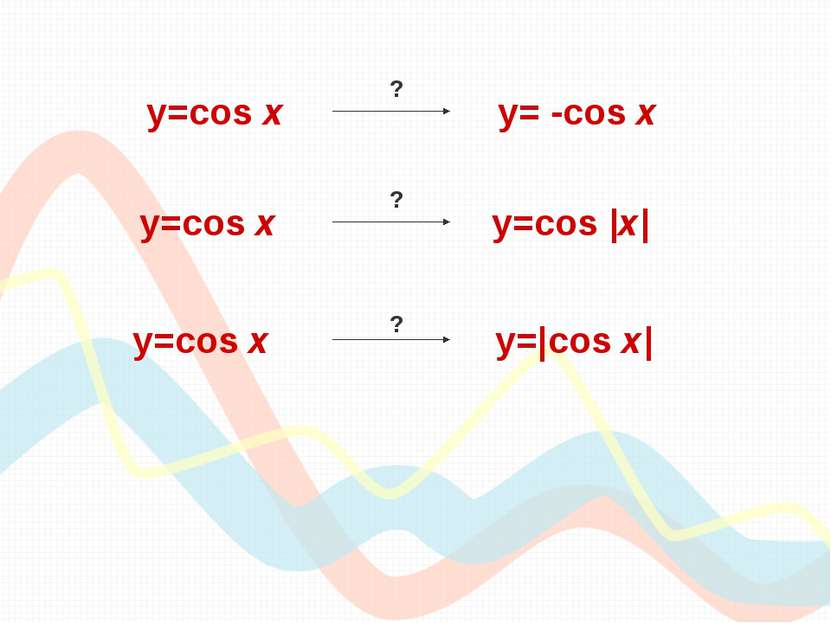
y=cos х y= -cos x Для того, чтобы из графика функции y=cos x получить график функции y= - cos x , необходимо выполнить симметрию исходного графика относительно оси «ох». ? y=cos х y= -cos x
Cлайд 10
y=cos х y=cos |x| Для того, чтобы из графика функции y=cos x получить график функции y=cos |x|, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а это и будет сам график y=cos x. ? y=cos х y=cos |x|
Cлайд 11
y=cos х y=|cos x| Для того, чтобы из графика функции y=cosx получить график функции y=|cos x|, необходимо сохранить ту часть исходного графика, где у≥0, и выполнить симметрию относительно «ох» той части, где у
Cлайд 12
y=cos х y=|cos |x|| Для того, чтобы из графика функции y=cosx получить график функции y=|cos|x||, необходимо сохранить ту часть исходного графика, где х≥0, и выполнить её симметрию относительно «оу», а затем сохранить ту часть получившеюся графика, где у≥0, и выполнить её симметрию относительно «ох» той части, где у
Cлайд 13
y=cos х y=cos 3x y=cos 3x График этой функции проходит через точки: ? х 0 у 1 0 -1 0 1 0 -1 0 -1 0 1 0 -1
Cлайд 14
y=cos х y=cos 3x Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos 3x, необходимо сжать исходный график в 3 раза вдоль «ох». ? y=cos х y=cos 3x
Cлайд 15
y=cos х y=cos x/3 y=cos x/3 График этой функции проходит через точки: ? х 0 у 1 0,5
Cлайд 16
y=cos х y=cos x/3 Вывод: Для того, чтобы из графика функции y=cos x получить график функции y=cos x/3, необходимо выполнить растяжение исходного графика в 3 раза вдоль оси «ох». ? y=cos х y=cos x/3
Cлайд 17
y=cos х y=3cos x y=3cos x График проходит через точки: ? х 0 у 3 1,5 0 -1,5 -3 1,5 0 -1,5 -3
Cлайд 18
y=cos х y=3cos x Вывод: Для того, чтобы из графика функции y=cos x получить график функции y=3cos x, необходимо растянуть исходный график в 3 раза вдоль оси «оу». ? y=cos х y=3cos x
Cлайд 19
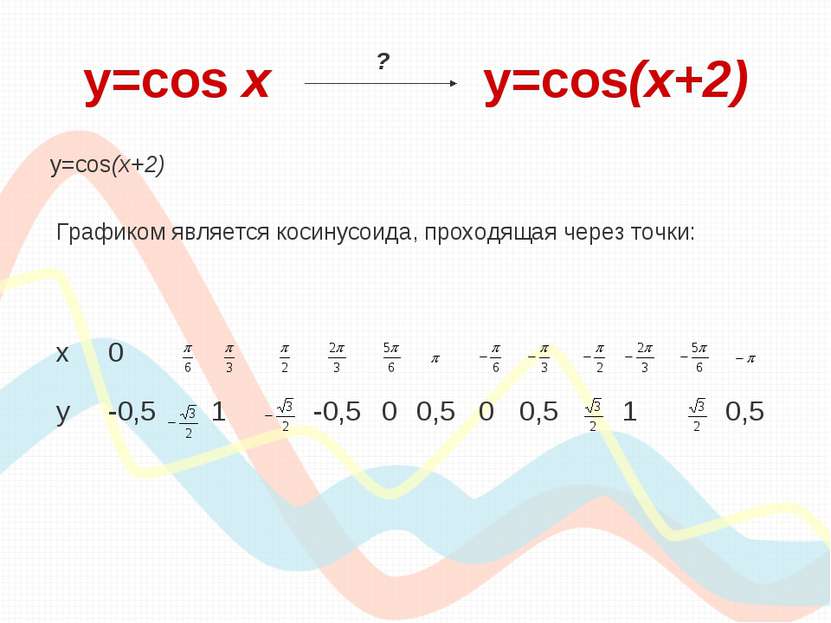
y=cos х y=cos(x+2) y=cos(x+2) Графиком является косинусоида, проходящая через точки: ? х 0 у -0,5 1 -0,5 0 0,5 0 0,5 1 0,5
Cлайд 20
y=cos х y=cos(x+2) Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos(x+2) , необходимо сдвинуть исходный график вдоль оси «ох» на 2 единицы влево. ? y=cos х y=cos(x+2)
Cлайд 21
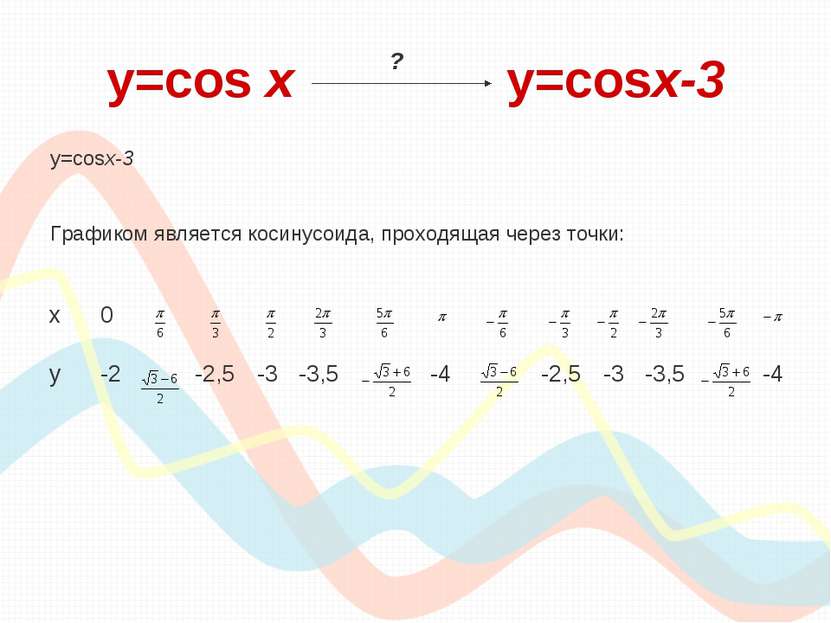
y=cos х y=cosx-3 y=cosx-3 Графиком является косинусоида, проходящая через точки: ? х 0 у -2 -2,5 -3 -3,5 -4 -2,5 -3 -3,5 -4
Cлайд 22
y=cos х y=cosx-3 Вывод: Для того, чтобы из графика функции y=cosx получить график функции y=cos x -3, необходимо сдвинуть исходный график вдоль оси «оу» на 3 единицы вниз. ?
Cлайд 23
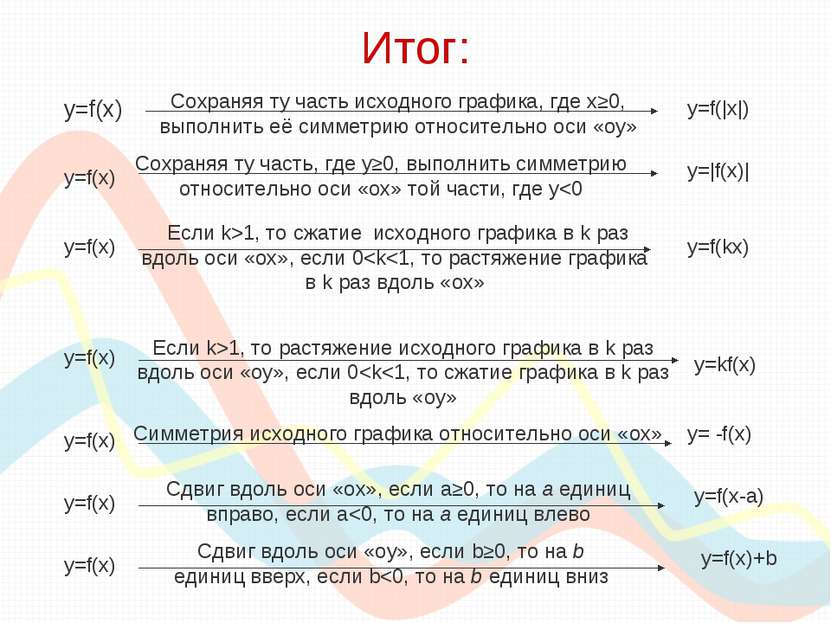
Итог: y=f(x) y=f(|x|) Сохраняя ту часть исходного графика, где х≥0, выполнить её симметрию относительно оси «оу» y=f(x) y=|f(x)| Сохраняя ту часть, где у≥0, выполнить симметрию относительно оси «ох» той части, где у1, то сжатие исходного графика в k раз вдоль оси «ох», если 0
Cлайд 24
Мы знаем, что для того, чтобы из графика функции получить график функции необходимо растянуть исходный график в 4 раза вдоль оси «оу». Исследование количества корней уравнения: y=a 1. Графиком является косинусоида, проходящая через точки: 2. у=а – линейная функция. Графиком является прямая, параллельная оси «ох» и проходящая через точки (2;а) и (0;а). х 0 у 1 0,5 0 -0,5 -1
Cлайд 25
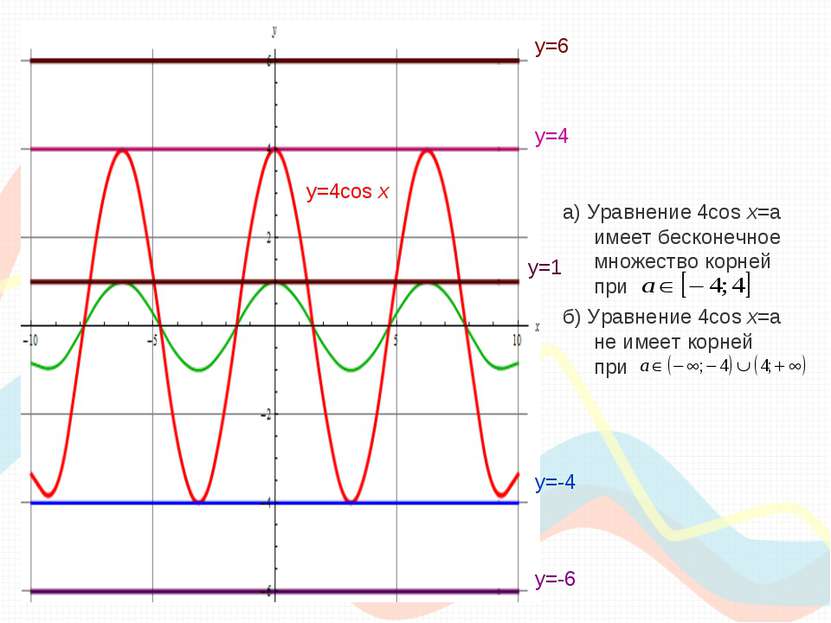
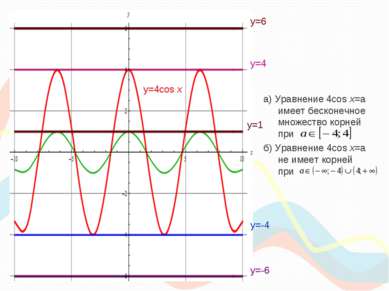а) Уравнение 4cos x=a имеет бесконечное множество корней при б) Уравнение 4cos x=a не имеет корней при y=4cos x y=6 y=4 y=1 y=-4 y=-6
Cлайд 26
Исследование количества корней уравнения: |cos 2x|=x² y=|cos 2x| y=cos x y=cos 2x y=|cos 2x| Мы знаем, что для того, чтобы из графика функции y=cos x получить график функции y=cos 2x, необходимо сжать исходный график в 2 раза вдоль оси «ох», а затем, чтобы получить график функции y=|cos 2x|, необходимо сохранить ту часть графика, где у≥0, и выполнить симметрию относительно оси «ох» той части, где у
Cлайд 27
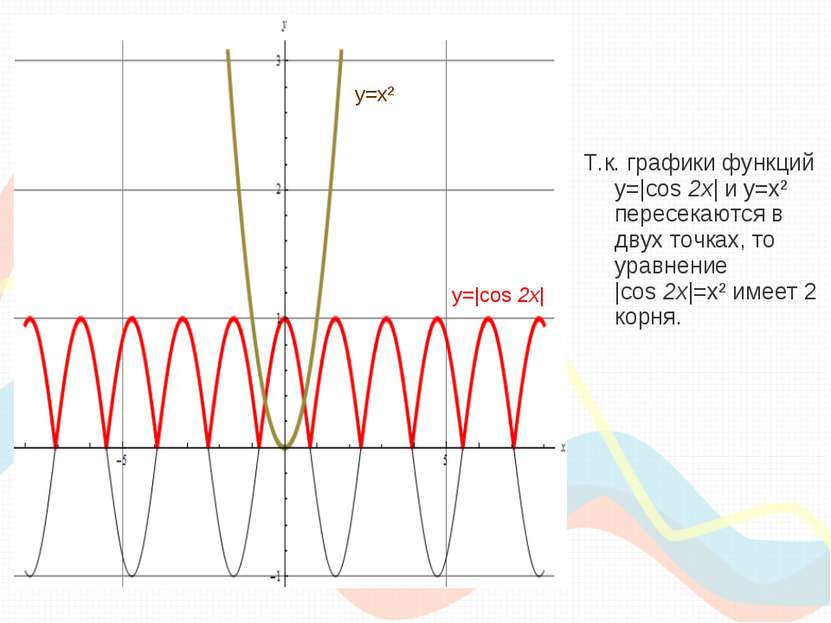
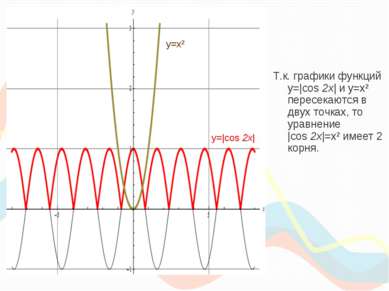Т.к. графики функций y=|cos 2x| и y=x² пересекаются в двух точках, то уравнение |cos 2x|=x² имеет 2 корня. y=|cos 2x| y=x²
Cлайд 28
Функции, использованные для построения рисунка
Cлайд 29
Cлайд 30
Cлайд 31
Microsoft Office Excel и Open Office Calc Wolfram Mathematica 1. Чтобы построить график функции необходимо указать список значений переменной «х», а затем ввести формулу для вычисления переменной «у». Только потом можно строить график. 1. В отличие от других систем Mathematica применяет разумную автоматизацию. То есть достаточно выбрать необходимую команду, ввести функцию и указать её область значений, а затем программа сама построит график. 2. Как следствие из первого пункта, на построение графиков затрачивается большое количество времени. - 2. Исходя из первого пункта, можем сделать вывод, что на построение графиков затрачивается совсем немного времени. 3. Существует один способ построения графиков (мастер диаграмм – график или точечная) 3. Есть несколько способов построения графиков функций (Plot, ListPlot и т.д.).
Cлайд 32
4. Чтобы каким-либо образом видоизменить график, необходимо зайти в меню «Диаграмма». Там указаны все возможные способы видоизменений графика. 4. Большинство различных видоизменений графика соответствует определённой опции, наименование которой необходимо знать наизусть или найти в справочном материале. 5. Интерфейс сложнее, чем в Mathematica и занимает большее пространство. 5. Интерфейс пакета значительно упрощён по сравнению с другими программами. Он строится из нескольких базовых понятий: Тетрадь, Ячейка и Палитра. Поэтому, работая в этой системе, можно убрать всё ненужное и оставить только необходимое. 6. Не возникло трудностей с построением, т.к. всё уже знакомо. + и - 6. При построении графиков у меня возникли трудности, потому что мы впервые столкнулись с этой программой, многое расположено в других местах и метод построения графиков совершенно новый. и Но с опытом работы этот способ построения стал доступным и более лёгким.
Cлайд 33
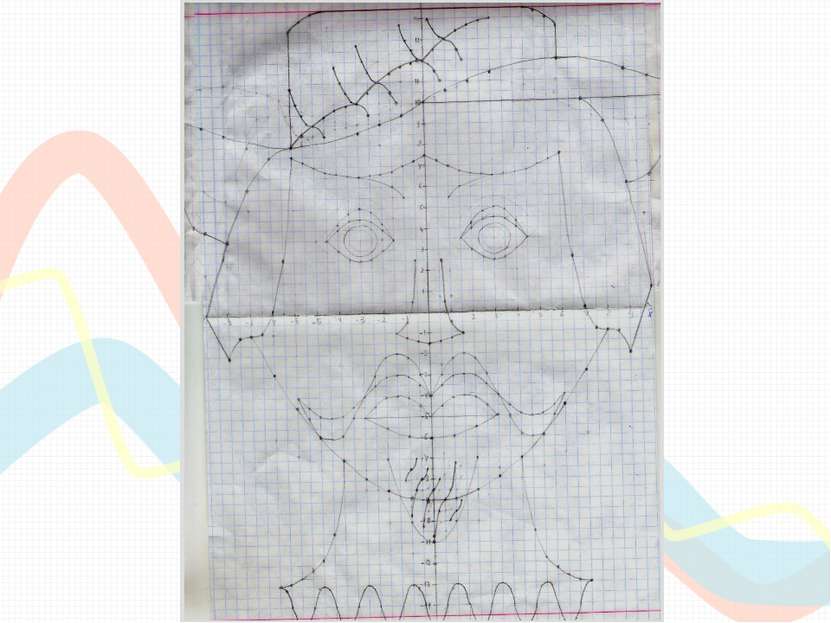
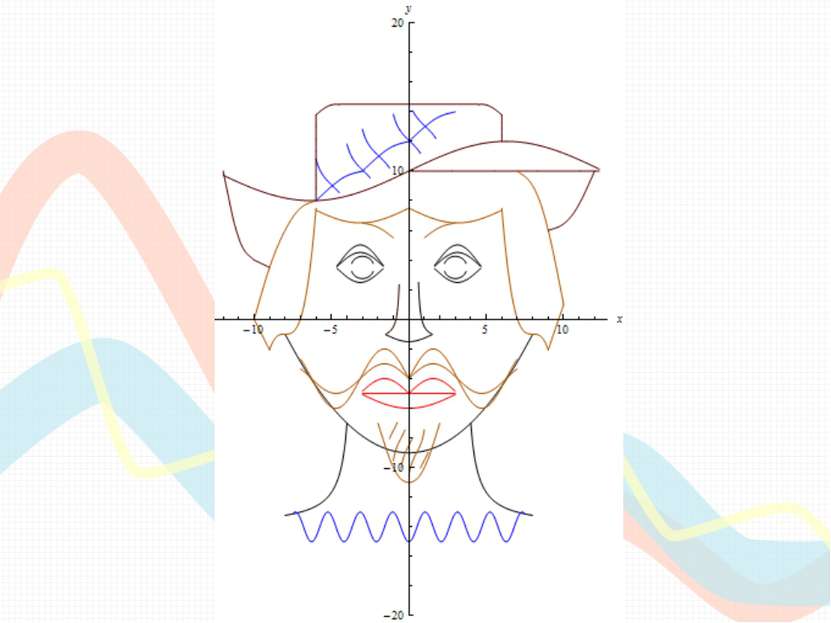
Заключение Цель достигнута, мы изучили способы построения графиков функций с помощью различных преобразований. Задачи выполнены, мы исследовали взаимосвязь графика функции y=f(x) с графиками функций y=|f(x)|, y=f(|x|) , y=f(kx), y=kf(x), y= -f(x), y=f(x)+b, y=f(x-a),научились строить эти графики, рассмотрели задания с применением таких функций, построили лицо мушкетёра, используя исследуемые функции, выяснили с помощью каких программных средств кроме Excel и Calc можно строить графики функций, выявили, в чём их преимущества и недостатки. Теперь мы знаем, что для построения графиков используется не только Microsoft Office Excel и Open Office Calc, но есть и другие программы, не только не уступающие по возможностям этим программам, но и превышающие их, например,Wolfram Mathematica.
Cлайд 34
Значимость полученных результатов: сейчас нам стало известно, как строить графики сложных функций с помощью преобразований графика исходной функции, и если встретятся задания с применением этих функций, то мы будем знать, как они выполняются. Использовать эти результаты можно при решении заданий единого государственного экзамена.
Cлайд 35
Спасибо за внимание!
