X
Код презентации скопируйте его
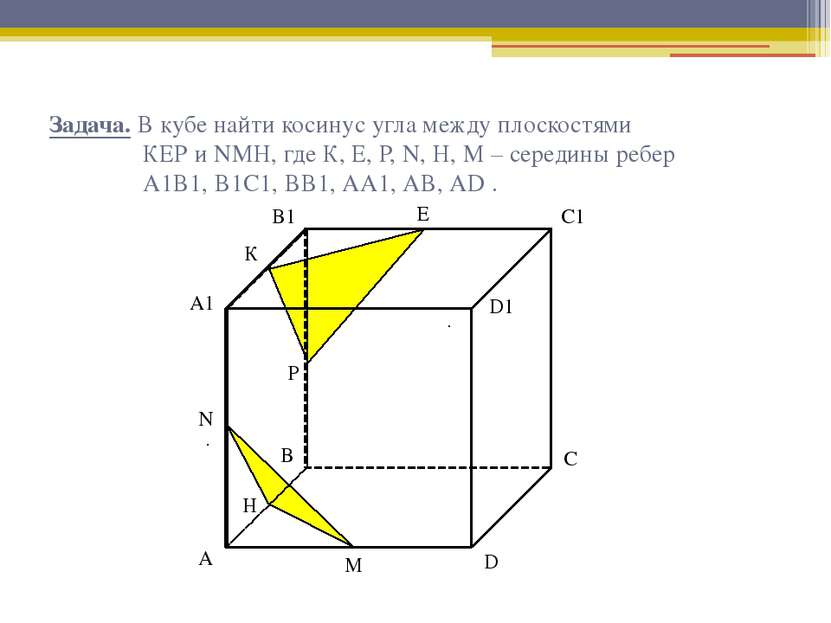
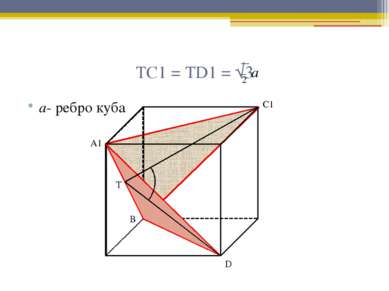
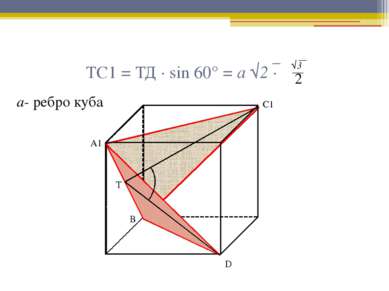
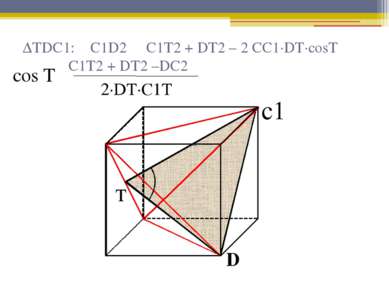
Угол между плоскостями
Скачать эту презентацию
Презентация на тему Угол между плоскостями
Скачать эту презентациюCлайд 1
Угол между плоскостями Решение задач уровня С. Муниципальное общеобразовательное учреждение средняя общеобразовательная школа №85 г.о. Тольятти учитель математики высшей категории Баленко Тамара Борисовна
Cлайд 2
Данная тема актуальна, так как подобные задачи требуют развитого абстрактного мышления. Задачи, представленные ниже, чаще всего вызывают затруднения при решении у учащихся. Наглядное решение позволяет лучше усвоить приемы решения таких задач. Нахождение угла между скрещивающимися прямыми и угла между плоскостями
Cлайд 3
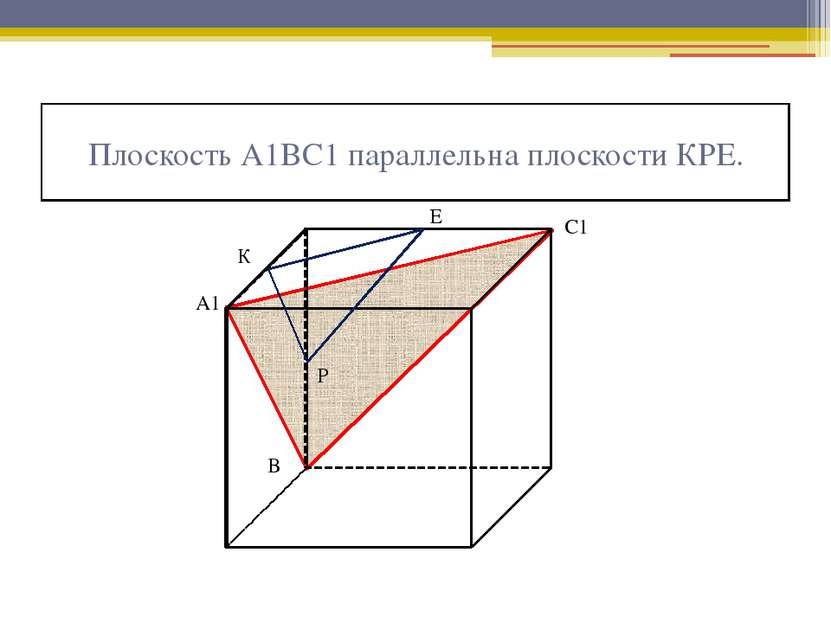
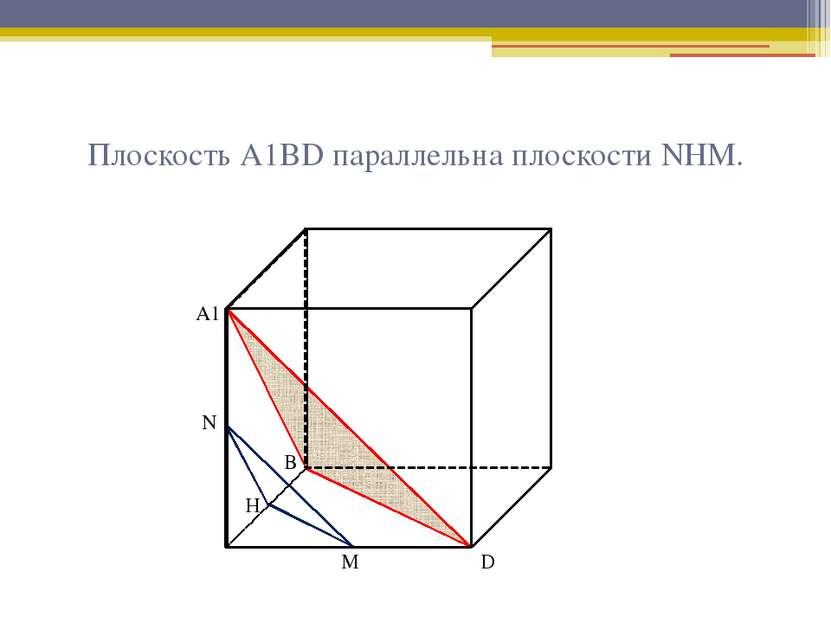
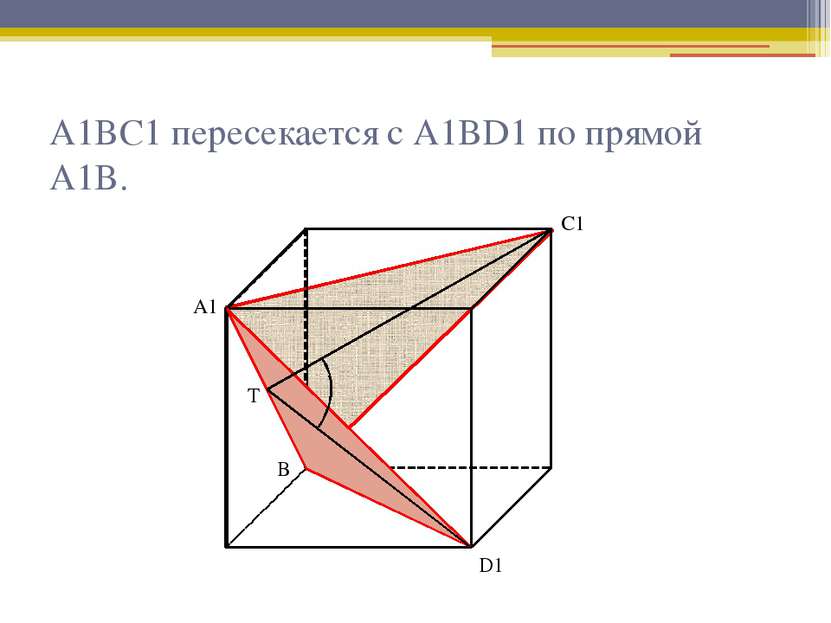
Аргументы 1. Определение куба. 2. Определение правильной призмы. 3. Свойства правильной призмы. 4. Свойство средней линии треугольника. 5. Признак параллельности плоскостей. 6. Определение угла между плоскостями. 7. Линейный угол двугранного угла. 8. Теорема Пифагора. 9. Теорема косинусов.
Cлайд 4
Задача. В кубе найти косинус угла между плоскостями КЕР и NМН, где К, Е, Р, N, Н, М – середины ребер А1В1, В1С1, ВВ1, АА1, АВ, АD . А А1 В1 С1 С D D1 В К Е Р N М H
Cлайд 5
Плоскость А1ВС1 параллельна плоскости КРЕ. К Е Р А1 В С1
Cлайд 6
Плоскость А1ВD параллельна плоскости NНМ. А1 В D Н М N
Cлайд 7
А1ВС1 пересекается с А1ВD1 по прямой А1В. А1 С1 Т D1 В
Cлайд 8
Найдем линейный угол двугранного угла С1А1ВD1. А1 С1 Т D1 В
Cлайд 9
В плоскости А1ВС1 проведем С1Т перпендикулярно А1В. А1 В С1 Т
Cлайд 10
В плоскости А1ВD проведем DТ перпендикулярно А1В А1 В D Т
Cлайд 11
Угол С1ТD- линейный угол двугранного угла С1А1ВD. А1 С1 Т D В
Cлайд 12
Найдем косинус угла С1ТD. А1 С1 Т D В
Cлайд 13
ТС1 = ТD1 = √3 а- ребро куба А1 С1 Т D В 2 а
Cлайд 14
ТС1 = ТД · sin 60° = а √2 · А1 С1 Т D В √3 2 а- ребро куба
Cлайд 15
ΔTDC1: C1D2 ₌ C1T2 + DT2 – 2 CC1∙DT∙cosT C1T2 + DT2 –DC2 2∙DT∙C1T cos T₌ т с1 D
Cлайд 16
Находим cos T: сosT₌ ₌ ₌ Ответ: . .
Cлайд 17
Спасибо за внимание.
