X
Код презентации скопируйте его
Теорема Фалеса
Скачать эту презентацию
Презентация на тему Теорема Фалеса
Скачать эту презентациюCлайд 1
Урок на тему: Теорема Фалеса Автор: Дятченко Татьяна Юрьевна Учитель математики ГОУ СОШ № 15
Cлайд 2
Цель и задача урока Цель данного урока знакомство с жизнедеятельностью философа и мыслителя Фалеса и его теоремой; развитие «геометрического зрения», расширение кругозора в плане знакомства с историей развития математики. Задачи: - продемонстрировать возможности применения теоремы Фалеса в различных геометрических задачах - расширить представления о сферах применения полученных математических знаний; - познакомиться с историческими сведениями об ученом Фалесе, о развитии математических знаний и их применениях
Cлайд 3
Фалес Фалес из Милета - первый древнегреческий мыслитель. По-видимому, он жил в 640-546 годах до н.э. Он первый применил доказательство теорем и ввел их в обиход математики. Основатель милетской школы. Считался первым из Семи мудрецов Греции.
Cлайд 4
Фалес считается родоначальником античной и, как следствие, европейской философии и науки. Считался первым из Семи мудрецов Греции. Важнейшей заслугой Фалеса в области математики должно быть перенесенное им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалесу открытие следующих геометрических предложений: ▪ Вертикальные углы равны. ▪ Углы при основании равнобедренного треугольника равны. ▪ Треугольник определяется стороной и прилежащими к ней двумя углами. ▪ Диаметр делит круг на две равные части.
Cлайд 5
Теорема Фалеса Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне
Cлайд 6
Доказательство: Пусть А3ОВ3 – заданный угол, а А1В1, А2В2, и А3В3– попарно параллельные прямые и А1А2=А2А3. Докажем, что В1В2=В2В3. Проведем через точку В2 прямую С1С2 параллельную прямой А1А3. По лемме А1А2 =С1В2, А2А3 = В2С2 и с учетом условия теоремы С1В2 = В2С2. Кроме того, В1С1В2 = В2С2В33– как внутренние накрест лежащие при параллельных прямых А1В1, А3В3 и секущей С1С2 , а В1В2С1 = С2В2В3 как вертикальные. По второму признаку равенства треугольников В1С1В2 = В3С2В2. Отсюда В1В2 = В2В3. Теорема доказана.
Cлайд 7
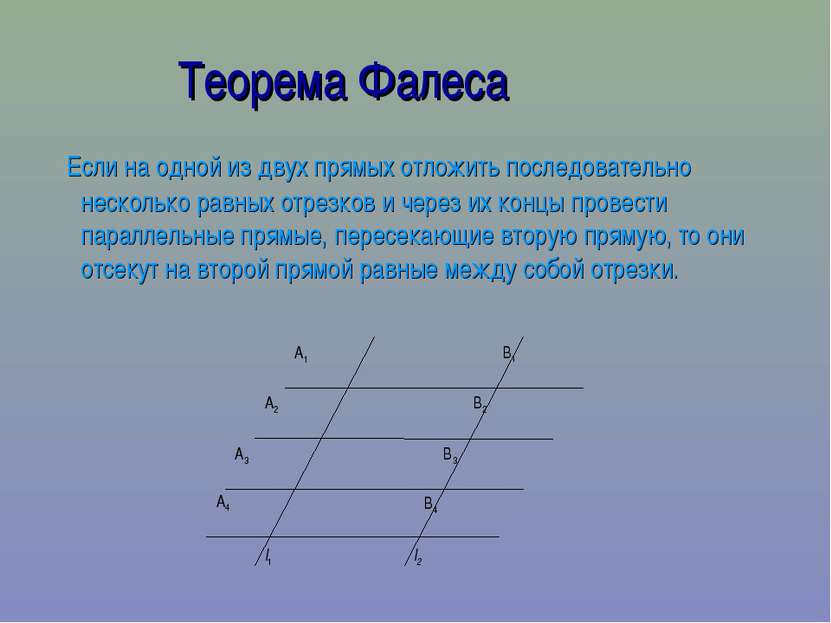
Теорема Фалеса Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные между собой отрезки.
Cлайд 8
Доказательство: Пусть на прямой l 1 отложены равные отрезки A1A2, A2A3, А3А4 и через их концы проведены параллельные прямые, которые пересекают прямую l 2 в точках B1, B2, B3, В4 как рисунке 4. Требуется доказать, что отрезки B1B2, B2B3, В3В4 равны друг другу. Докажем, что B1B2=B2B3. Рассмотрим случай, когда прямые l 1 и l 2 параллельны. Тогда A1A2=B1B2 и A2A3=B2B3 как противоположные стороны параллелограммов A1B1B2A2 и A2B2B3A3. Так как A1A2= A2A3, то и B1B2=B2B3. Теорема доказана.
Cлайд 9
Применение теоремы Фалеса к решению задач Средняя линия треугольника Средняя линия треугольника, соединяющая середины двух данных сторон, параллельна третьей стороне и равна ее половине.
Cлайд 10
Доказательство: Пусть отрезок DE – средняя линия в треугольнике ABC, т.е. AE = EC, CD = BD. Проведем через точку D прямую a, параллельную стороне AB. По теореме Фалеса прямая a пересекает сторону AC в ее середине и, следовательно, содержит среднюю линию DE. Значит, средняя линия DE параллельна стороне AB. Проведем среднюю линию DF. Она параллельна стороне AC. Тогда по лемме отрезок ED равен отрезку AF и равен половине отрезка AB. Теорема доказана.
Cлайд 11
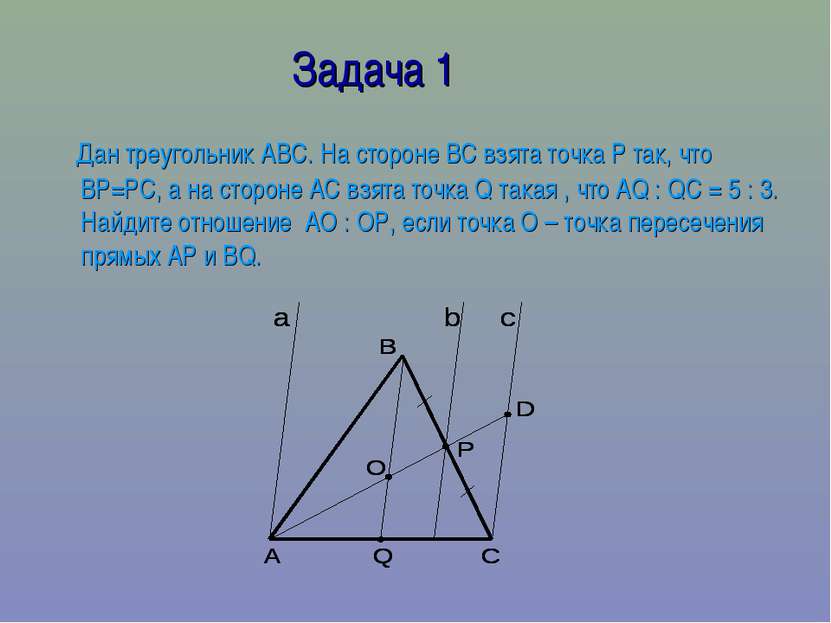
Задача 1 Дан треугольник АВС. На стороне ВС взята точка Р так, что ВР=РС, а на стороне АС взята точка Q такая , что АQ : QС = 5 : 3. Найдите отношение АО : ОР, если точка О – точка пересечения прямых АР и ВQ.
Cлайд 12
Решение: Проведем прямые параллельные ВQ через точки А, Р и С. Точка D – это точка пересечения прямых АР и с. По теореме Фалеса параллельные прямые ВQ, b и c, которые отсекают равные отрезки ВР и РС, отсекают равные отрезки ОР и РD на прямой АD. По теореме Фалеса параллельные прямые a, BQ и с, которые отсекают на прямой АС отрезки в соотношении 5 : 3, отсекают и на прямой АD отрезки в соотношении 5 : 3. То есть AQ : QC= 5:3 и AO : OD = 5:3, а отрезок OD=2OP. Следовательно, AO : OP = 10:3. Ответ: 10 : 3.
Cлайд 13
Задача 2 Разделите отрезок АВ при помощи циркуля и линейки на n равных частей.
Cлайд 14
Решение: Проведем луч AX, не лежащий на прямой AB, и на нем от точки A отложим последовательно n равных отрезков АА1, А1А2, …,Аn-1An , т.е. на столько равных отрезков, на сколько равных частей нужно разделить данный отрезок AB. Проведем прямую AnB (точка Аn – конец последнего отрезка) и построим прямые, проходящие через точки A1, A2,…, An-1 и параллельные прямые прямой AnB. Эти прямые пересекают отрезок AB в точках B1, B2, …, Bn-1, которые по теореме Фалеса делят отрезок AB на n равных частей.
Cлайд 15
Задача 3 Разделите данный отрезок АВ на два отрезка АХ и ХВ, пропорциональные данным отрезкам P1Q1 и P2Q2.
Cлайд 16
Решение: Проведем какой-нибудь луч АМ, не лежащий на прямой АВ, и на этом луче отложим последовательно отрезки АС и CD, равные отрезкам P1Q1 и P2Q2. Затем проведем прямую BD и прямую, проходящую через точку С параллельно прямой BD. Она по теореме Фалеса пересечет отрезок АВ в искомой точке Х.
Cлайд 17
Заключение: В представленной работе рассмотрена теорема величайшего математика – ученого – мыслителя Фалеса, задачи, в решении которых применяется различные варианты этой теоремы. Решение геометрических задач различными способами является исследовательской частью данного урока и дает возможность сравнить разные способы решения и проанализировать их появление.
